P1002 [NOIP2002 普及组] 过河卒

题目描述

棋盘上 A 点有一个过河卒，需要走到目标 B 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 C 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，A 点 (0,0)、B 点 (n,m)，同样马的位置坐标是需要给出的。

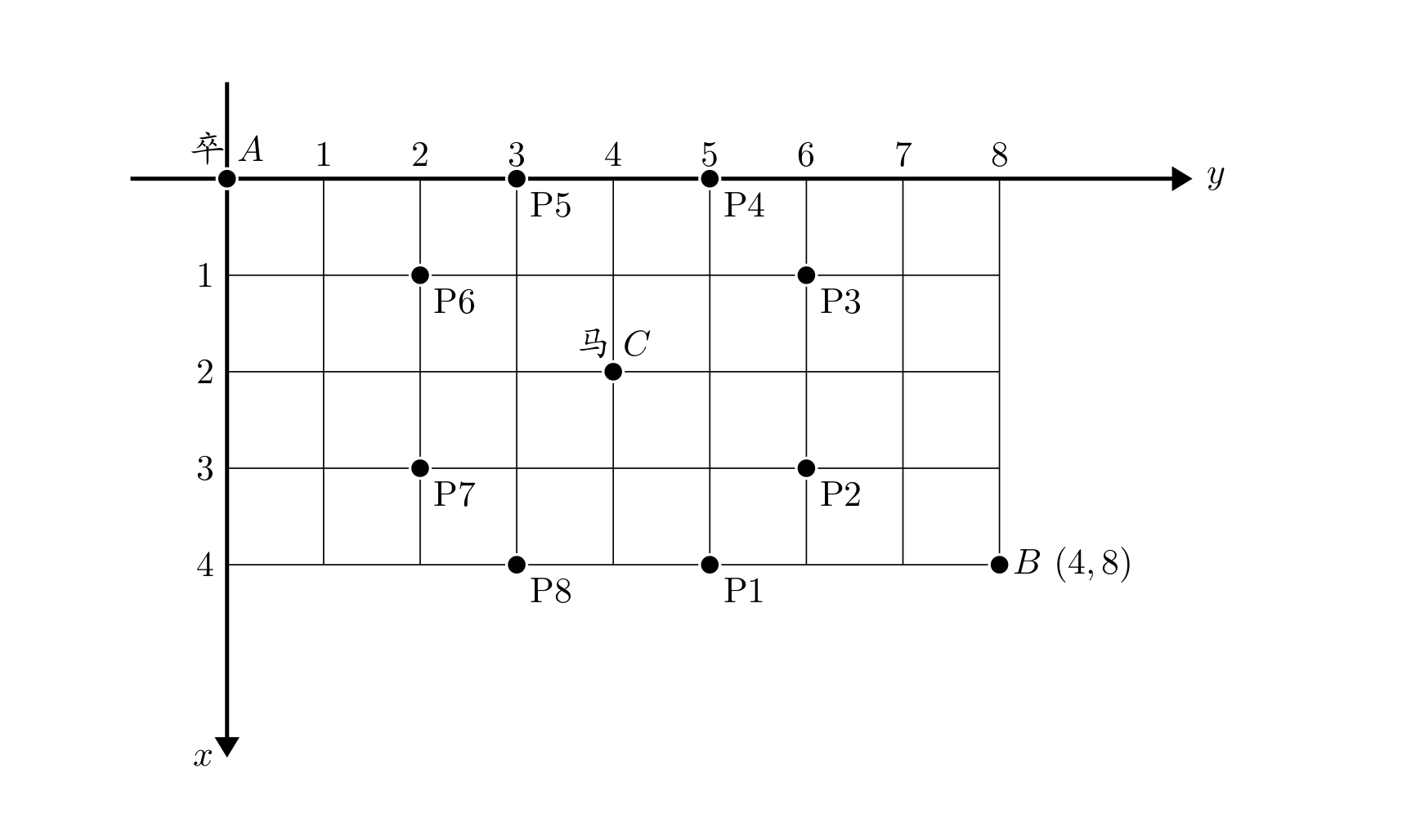
现在要求你计算出卒从 A 点能够到达 B 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式

一行四个正整数，分别表示 B 点坐标和马的坐标。

输出格式

一个整数，表示所有的路径条数。

输入输出样例

输入 #1

6 6 3 3

输出 #1

6

说明/提示

对于 100% 的数据，1≤n,m≤20，0≤ 马的坐标 ≤20

思路：

这道题与P1255 数楼梯的思路是一致的，不过不同的是这道题是二维的，数楼梯是一维的问题，

如果对P1255 数楼梯中的一维的办法还不太理解的话，可以先去看看我之前的文章P1255 数楼梯

那么我们直接讲二维的思路了，这题要求到达从左上角的点，到达右下角的点可能的步数，同时存在有对方马的控制点，这些点我们就不可以经过。

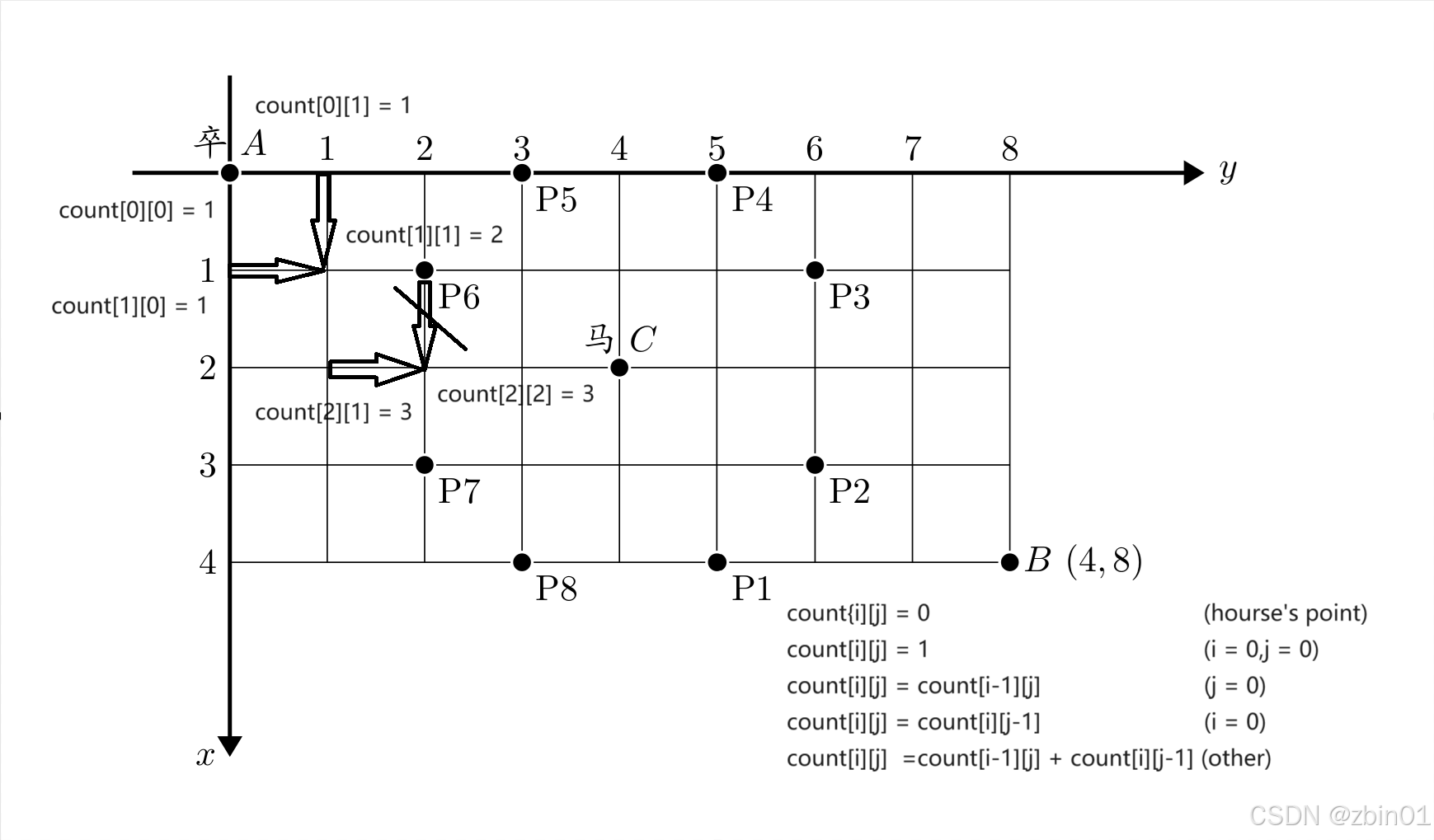
左上角的点我们记为（0，0），右下角的点就是（x，y），注意不是（x-1，y-1），仔细观察题目的图，所以这里很容易犯错的就是建立数组时，我们要x+1和y+1，因为数组是从0开始的。我们建立一个二维数组count，count（i，j）表示从起点到（i，j）的路径数，我们初始化count（0，0） = 1，有题目可以知道过河卒只能向下和向右走，所以count（i，j）的步数只由count（i-1，j）和count（i，j-1）来决定，所以count（i，j）也就等于count（i-1，j）与count（i，j-1)之和，即count（i，j）=count（i-1，j）+ count（i，j-1) 。

同时来处理对方马的控制点，我们只需创建两个数组，代表以马的坐标为中心，各个控制点x方向和y方向的变化就可以实现，记录下马的所有控制点。在设置完所有对方马的控制点后，将这些点的count设置为0，同时当在遍历的时候如果遇到这些点，直接跳过此次循环，进入下一次循环。

最后注意一下边界的情况，边界就只有一边可以到达，左边界的只受上一格的步数影响，上边界的只受左一格的步数影响。所以当i = 0 或者 j = 0的时候，我们只需将count[i][j] = count[i][j-1] 或者 count[i][j] = count[i-1][j]就可以了。

最后以图的形式再呈现一下。 

接下来就是代码的呈现咯！

AC代码

#include<iostream>
using namespace std;
typedef long long ll;
int X[9] = { -2,-2,-1,-1,0,1,1,2,2 };//模拟对方马的控制点
int Y[9] = { -1,1,-2,2,0,-2,2,-1,1 };
void solve()
{
	int n, m, x, y;
	cin >> n >> m >> x >> y;
	ll** vec = new ll* [n+1];
	for (int i = 0; i < n+1; i++) {
		vec[i] = new ll[m+1];
	}
	for (int i = 0; i <= n; i++) {
		for (int j = 0; j <= m; j++) {
			vec[i][j] = 1;
		}
	}
	for (int i = 0; i < 9; i++) {
		if (x + X[i] >= 0 && x + X[i] <= n && y+Y[i]>= 0 && y+Y[i] <= m) {
			vec[x + X[i]][y + Y[i]] = 0;
		}
	}
	for (int i = 0; i <= n; i++) {
		for (int j = 0; j <= m; j++) {
			if (i == 0 && j == 0) { continue; }
			if (vec[i][j] == 0) { continue; }//跳过
			if (i == 0) {
				vec[i][j] = vec[i][j - 1];
			}
			if (j == 0) {
				vec[i][j] = vec[i - 1][j];
			}
			if (i != 0 && j != 0 && vec[i][j] != 0) {
				vec[i][j] = vec[i - 1][j] + vec[i][j - 1];
			}
		}
	}
	cout << vec[n][m];
    for(int i = 0;i < n+1;i++){
        delete[]vec[i];
    }
    delete[]vec;
}
int main()
{
	int t = 1;
	cin.tie(0)->ios::sync_with_stdio(false);
	while (t--) {
		solve();
	}
	return 0;
}