P1255 数楼梯-优快云博客

本文链接：https://blog.youkuaiyun.com/zbin01/article/details/140882730

题目描述

楼梯有 N 阶，上楼可以一步上一阶，也可以一步上二阶。

编一个程序，计算共有多少种不同的走法。

输入格式

一个数字，楼梯数。

输出格式

输出走的方式总数。

输入输出样例

输入 #1

输出 #1

说明/提示

对于 60% 的数据，N≤50；
对于 100% 的数据，1≤N≤5000。

思路

这道题的题干很简单，就是我们可以跳一步或者跳两步，然后求出到第n层有几种方式。

这道题有两种解决思路：动态规划和递归方法解决。我们先讲动态规划是怎么实现的。

动态规划思路

斐波那契数列

一开始大家可能没有什么头绪，我们要用什么方式才可以知道到第n层有几种方式呢？想不出来，那我们先列举一下，说不定就由思路了呢。第一层： 1，第二层： 2，第三层： 3，第四层： 5，第五层： 8，第六层： 13，第七层： 21，是不是有点感觉了，你看看 1，2，3，5，8，13,21这些数让你想起了谁，没错！就是斐波那契数列，斐波那契数列的特点是什么？这个数等于前两个数的和。然后大家再来想一想这道题，他只能跳一步或者两步，那么第i层的步数是不是只能由第i-2和i-1层的步数来决定，因为没有别的层可以到达第i层了，所以第i层的步数也就是i-1层步数和i-2步数之和。不过有一点点不一样，因为这道题第一层只能是平地跳一步到达，没有别的办法，而第二层可以是第一层跳一步加上平地跳两步，所以第二层是2，和斐波那契数列的1，1，2，3，5，8……不同，但是本质是一样的。

这里我也加了一个图便于大家理解，同一个颜色代表到达第i层的可能。

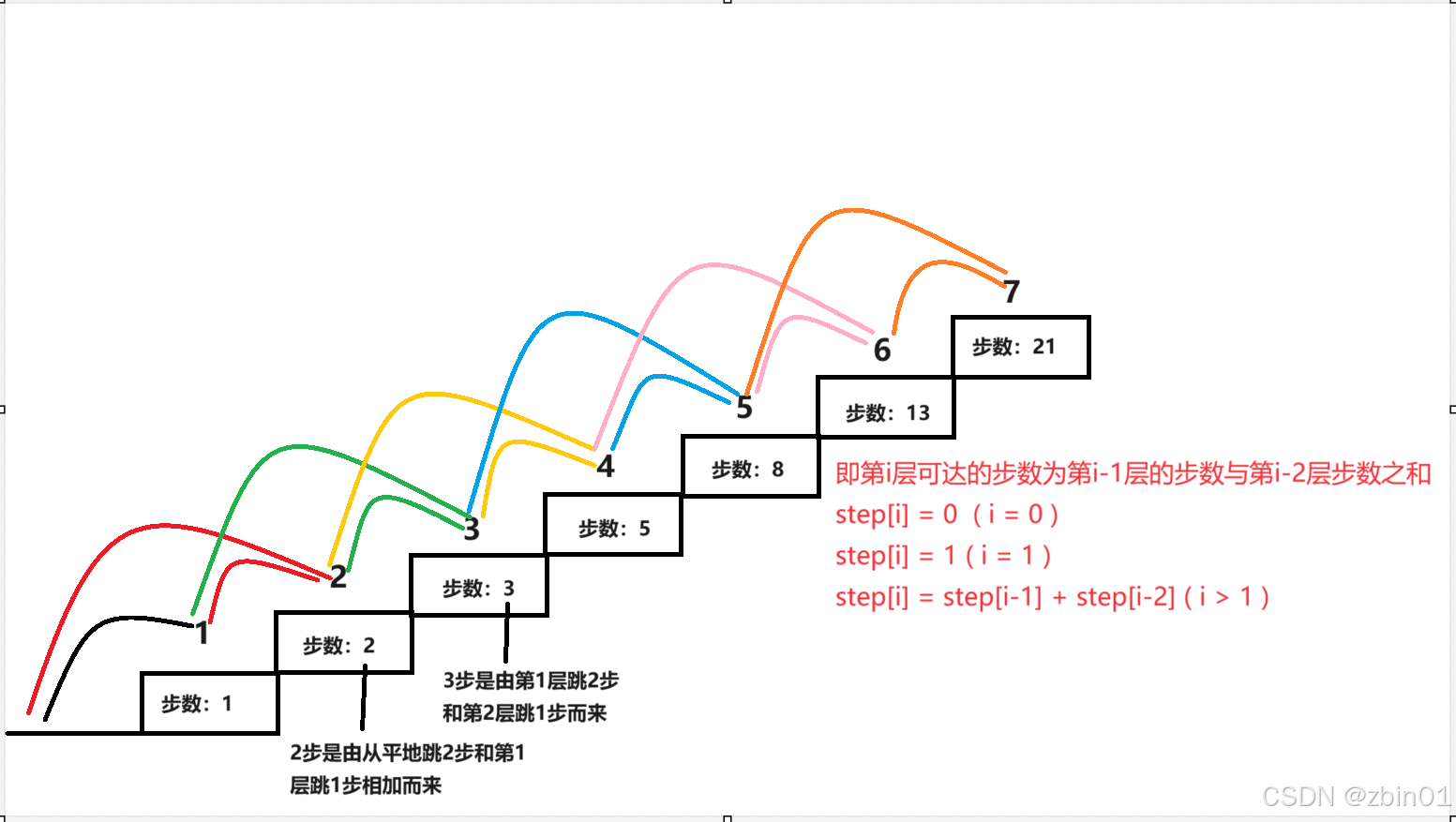
这一思路也就是所谓的动态规划了，动态规划是一种算法设计技巧，它用于解决具有重叠子问题和最优子结构特性的问题。其通常用于优化那些通过递归方法解决时会重复计算相同子问题的问题。

动态规划的关键概念

最优子结构：一个问题的最优解包含其子问题的最优解。这意味着问题可以分解成更小的子问题，而这些子问题的解可以用来构建原问题的解。

重叠子问题：在递归解决方案中，相同的子问题被多次解决。动态规划通过存储这些子问题的解来避免重复计算，这些存储的解称为“记忆”。

表格化：一般就是创建一个数组（二维情况较多），将每一个子问题记录下来，再依次解决更大的子问题，直到达到原始问题，我们通过一个数组记录数据，在需要的时候进行调用。

我们一点一点来解释，首先怎么理解最优子结构呢？

其实说的简单点就是 “ 我是怎么来的？”，像这道题除了前两个数，斐波那契数列的每一个数都是由前两个数之和而来的，那么我们要求第n个数时，我们可以讲这个问题拆分成第n-1和第n-2个数是怎么来的，第n-1个数的子问题还会再分解出子问题，依次分解，直到拆分到最小的子问题，已经不能拆分为止，在斐波那契数列中就是到求第1个或者第2个数为止。所以我们的问题是由其子问题组成的，同时也是由子问题来决定的，子问题的变化也就影响了主问题的变化，而我们最先能确定的只有最底层的子问题，只有当最底层的子问题是最优解，我们依次将子问题组合，主问题也才会是最优解。

其次为何在递归方法解决时会有重复子问题存在呢？

我们在刚刚开始学习的时候肯定有写过使用递归求斐波那契数列的方法。

#include<iostream>
using namespace std;
int Fibonacci(int x){
	if(x==1||x==2) return 1;
	else return Fibonacci(x-1) + Fibonacci(x-2);
}
int main() {
   	int n;
   	cin>>n;
   	cout<<Fibonacci(n);
    return 0;
}

代码如上，我们输入n，再将n带进函数Fibonacci中，然后就是像上文所说的依次划分为各个子问题，然后依次递归分解。那重复子问题在哪里呢？下面我画一张图给大家看看。

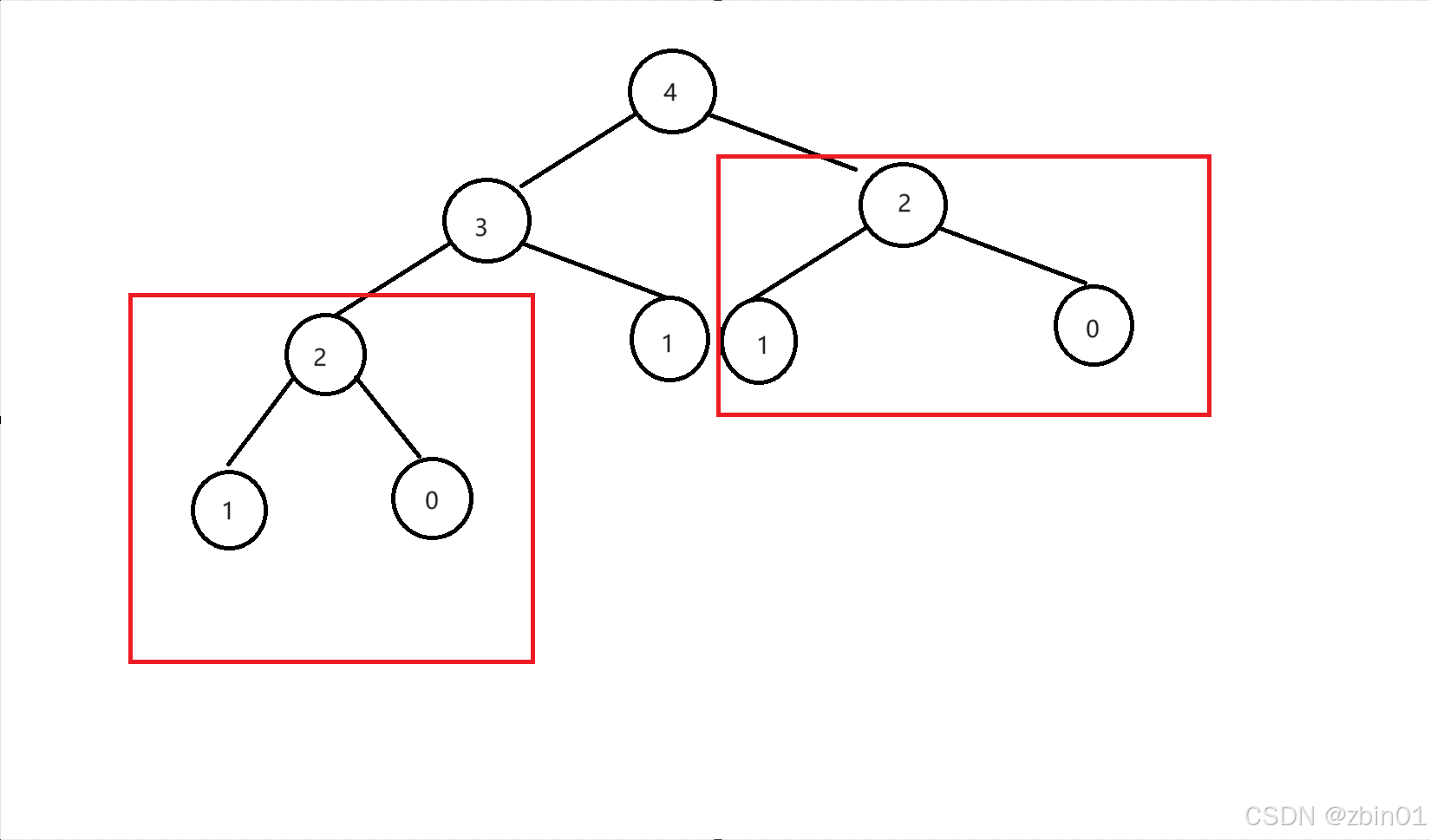
由图可以看出来如果要求第4层的步数时，我们就会有一部分在递归时是重复的，在第4层的时候需要分解成第2和第3层，而在第3层的时候又需要分解成第1层和第2层，这时第2层就重复计算了两次，这仅仅是第4层的时候，如果层数一变大，这样重复的地方会很多，那么就很浪费时间。

那要如何解决这个问题呢，就是在加上一个”记忆“的数组，记录下已经遍历过的层数，当之后再遇到这个层数时，直接使用即可。这样就不用一直重复递归。

接着咱来讲一下递推是什么实现的。

递推思路

递推的思路就比较简单了，所谓递推就是一步一步推向我们要解决的问题的答案。

这种递推的思路就是“我是怎么去的”

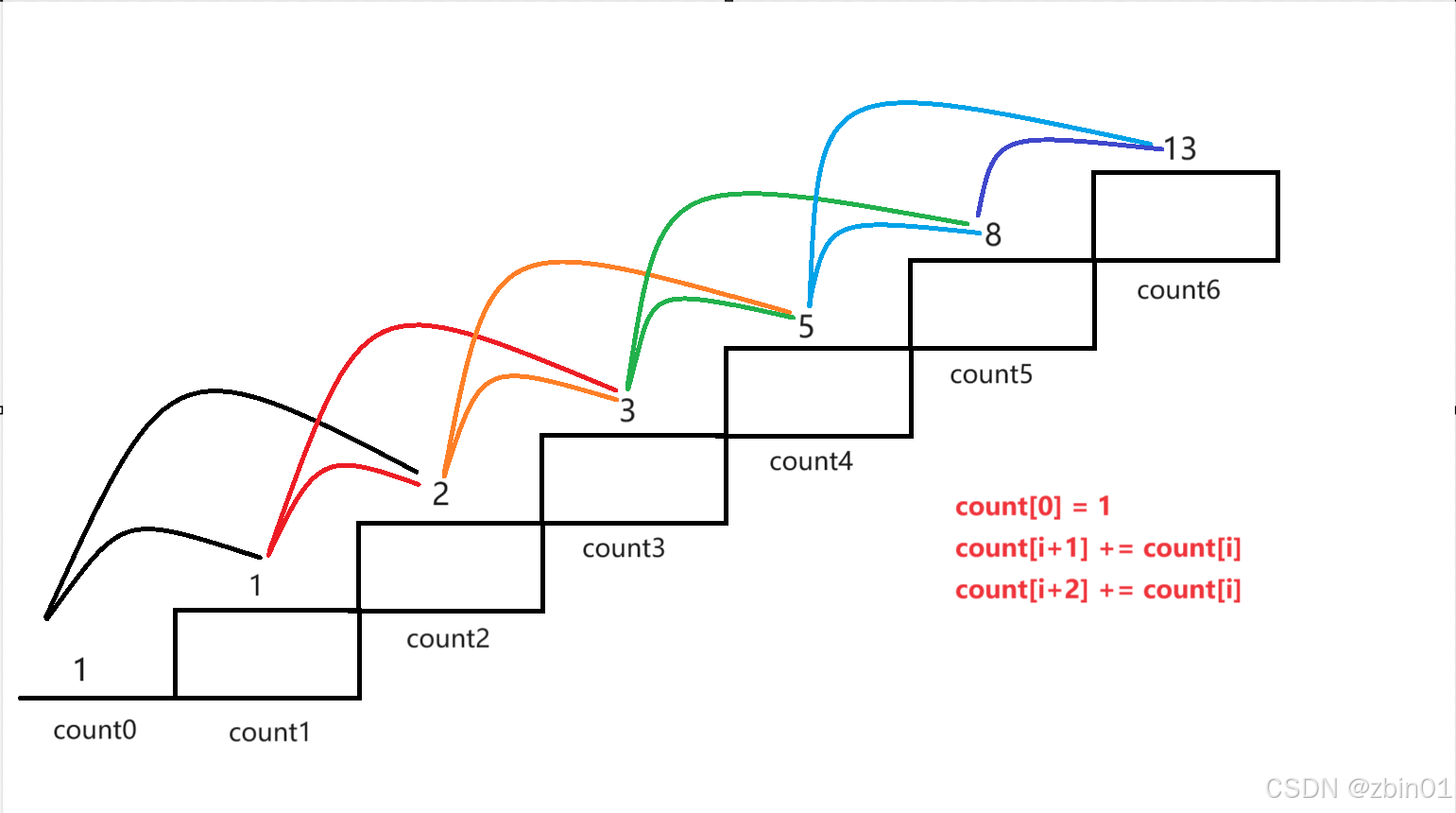
一开始我们还是开一个count数组，记录方案数，count[i]代表到达第i阶楼梯的方案数，初始值为0。我们先一层楼梯一层楼梯来试一试，在地板时我们只有一种方案，就是站在那里，所以count[0] = 1，接着在地板上我们向上走，我们可以走一步，那么count[1]+count[0](count[1] = 1),也可以走两步，那么count[2]也+count[0](count[2] = 1)，现在到了第1层，同样的，我们走一步，那么count[2]+count[1](count[2] = 2),要是走两步count[3]+count[1](count[3] = 1)，接着是第2层，走一步，count[3] += count[2](count[3] = 3)，走两步，count[4] += count[2](count[4] = 2) ……，我们可以看出规律，当我们在第i层楼梯时，第i+1和第i+2层楼梯都可以加上第i层楼梯的方案数，即

count[i+1] += count[i]

count[i+2] += count[i]

通过这个递推方程，我们就可以推导出第n层楼梯的方案数。还是再以图片的形式给大家更直观的呈现一下。

接下来就是将我们上述的思路转化为代码

代码呈现

动态规划

#include<iostream>
#include<vector>
using namespace std;
typedef long long ll;
int main() {
   	ll n;
	cin>>n;
	vector<ll> vec(n+1,0);
	vec[0] = 1;
	vec[1] = 1;
	for(ll i = 2;i<=n;i++){
		vec[i] = vec[i-1] + vec[i-2];
	}
	cout<<vec[n];
    return 0;
}

我们这里就是将上面的图写成代码的形式，建立一个long long数组vec，定义vec[0] = 1,vec[1] = 1,然后直接进行递推，最后输出vec[n]即可。

递推

#include<iostream>
#include<vector>
using namespace std;
typedef long long ll;
int main() {
   	ll n;
	cin>>n;
	vector<ll> vec(n+2,0);
	vec[0] = 1;
	for(int i = 0;i<n;i++){
		vec[i+1] += vec[i];
		vec[i+2] += vec[i];
	}
	cout<<vec[n];
    return 0;
}

我们有两种思路，怎么都不可能过不了，直接提交！

没过！！！为什么会这样呢，哪里出错了。原来是数据范围的关系，对于 60% 的数据，N≤50；对于 100% 的数据，1≤N≤5000。前面6个的N比较小，后四个可能是几百几千，那么这个数就很大很大了，如果连long long都越界的话要怎么办？没错，就是高精度，这道题我们还需要使用高精度来解决，至于高精度算法具体思路要怎么写，可以去参考我前面的那篇讲解高精度问题（这也是因为使用递推的原因之一）。

所以我们在原来的代码上加以修改，将记忆化数组变化为二维数组，行代表第几层，列代表数据的每一位。然后还加了一个全局变量len记录目前达到最大的长度是多少，因为是正数不断相加的，长度只会增不会减，其次在循环中，增加个if语句，a[t][i] > 9 就进位，if中还要一个判断，如果a[t][i]>9 同时 i == len 那么最大的长度就需要加一，接着就一直遍历到i = n为止，最后输出即可。

AC代码

动态规划：

#include<iostream>
using namespace std;
typedef long long ll;
int a[5002][5002];
int len = 1;
void sum(int t) {
    //先每位的数加起来
	for (int i = 1; i <= len; i++) {
		a[t][i] = a[t - 1][i] + a[t - 2][i];
	}
    //再进行进位
	for (int i = 1; i <= len; i++) {
		if (a[t][i] > 9) {
			a[t][i + 1] += a[t][i] / 10;//高精度加分的基本操作
			a[t][i] %= 10;
			if (i == len) {//一定得i==len才可以len++
				len++;
			}
		}
	}
}
int main()
{
	int n;
	cin >> n;
	a[1][1] = 1;
	a[2][1] = 2;//这里就直接将1，2都记录了，这个没什么太大关系的，要的话3也可以记录，由你喜好决定咯
	for (int i = 3; i <= n; i++) {
		sum(i);
	}
	for (int i = len; i >= 1; i--) {
		cout << a[n][i];
	}
	return 0;
}

递推：

#include<iostream>
using namespace std;
typedef long long ll;
int a[5002][5002];
int len = 1;
int main()
{
	int n;
	cin >> n;
	a[0][1] = 1;
	for (int i = 0; i < n; i++) {
		for (int j = 1; j <= len; j++) {
			a[i + 1][j] += a[i][j];
			a[i + 2][j] += a[i][j];
		}
		int t = i + 1;//当到第i层的时候，第i+1层已经加完了的，所以是将第i+1层进行进位
		for (int j = 1; j <= len; j++) {
			if (a[t][j] > 9) {
				a[t][j + 1] += a[t][j] / 10;//高精度加分的基本操作
				a[t][j] %= 10;
				if (j == len) {//一定得i==len才可以len++
					len++;
				}
			}
		}
	}
	for (int i = len; i >= 1; i--) {
		cout << a[n][i];
	}
	return 0;
}

大概就讲这么多咯，有问题可以提出来，我会尽可能为大家解答的，希望大家看完这篇能够有所收获。