频率分析和离散傅里叶变换——DSP学习笔记四

原创 于 2024-04-27 14:29:34 发布 · 802 阅读 · 3 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#信息与通信 #信号处理 #学习 #笔记

本文详细介绍了傅里叶变换的基本思想，包括如何将信号表示为不同频率正弦分量的组合，以及离散傅里叶变换（DFT）的概念、定义和重要性质。特别强调了DFT的高效实现，如FFT算法。此外，文章还涵盖了频谱分析中的步骤，如时域抽样、截短和频域抽样，以及线性卷积的DFT应用。

  • 背景知识

    • 四种基本的傅里叶变换

      • 基本思想：将信号表示为不同频率 正弦分量的线性组合

      • 正弦信号和复指数时间信号的有用特性

        • 相同频率但不同相位的正弦信号的任何线性组合，都是有着相同频率但不同相位，且幅度可能受改变的正弦信号。

        • 复指数时间信号不同延迟版本的任何线性组合，等于该信号乘以一个复系数，由复系数决定其幅度和相位的变化。

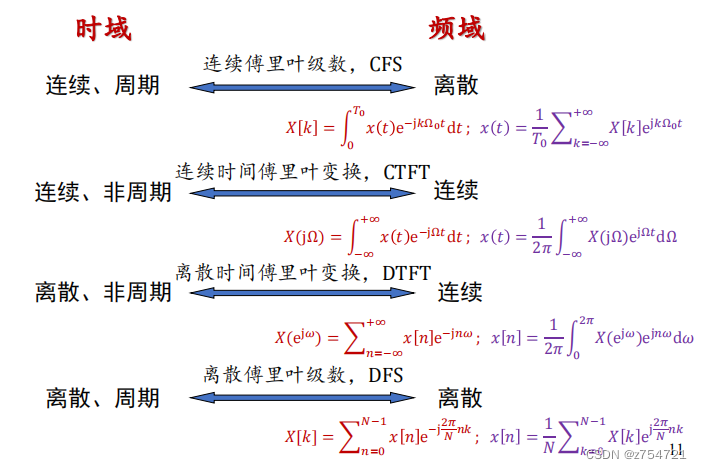
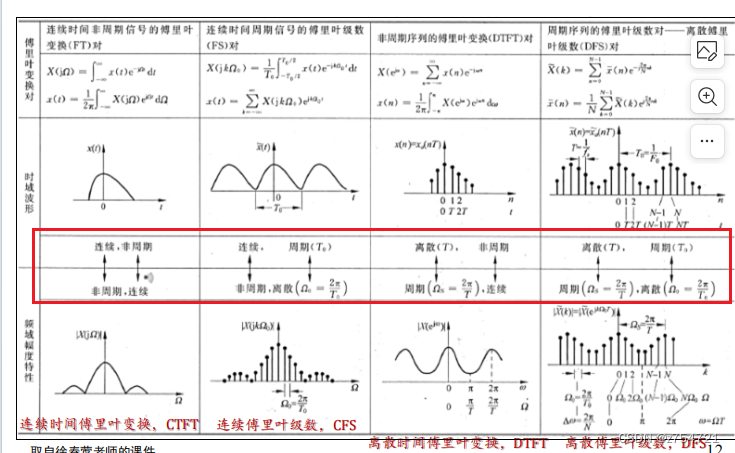
      • 四种常用的傅里叶变换

  • 离散傅里叶变换

    • DFT的定义

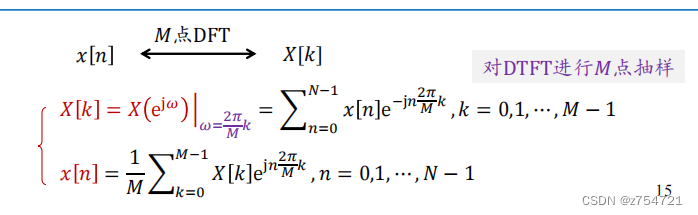
      • 频域抽样的分析：

        • 时域抽样导致频域上的周期延拓

        • 频域抽样导致时域上的周期延拓

          <
最低0.47元/天 解锁文章
数字信号处理(DSP)实验——离散傅立叶变换及谱分析
Safaearth的博客
04-12 1万+
一、实验目的 1.掌握离散傅里叶变换的计算机实现方法。 2.掌握计算序列的圆周卷积的方法。 3.学习用DFT对连续信号和时域离散信号进行谱分析的方法，了解可能出现的分析误差，以便在实际中正确应用DFT。 4. 理解用FFT对周期序列进行频谱分析时所面临的问题并掌握其解决方法。 5.掌握用时域窗函数加权处理的技术。 6.理解用FFT对非周期信号进行频谱分析所面临的问题并掌握其解决方法。 二、实验原理与方法 １. 对周期序列进行频谱分析应注意的问题 对时间序列作FFT时，实际上要作周期延拓（如果取长序列的一段
离散傅里叶变换(Example)
luixiao1220的博客
05-23 766
UTF8gbsn Introduction 在工程上，我们通常需要对离散的信号进行处理。所以我们必须要应用一种离散的傅里叶 变换。傅里叶级数的表示形式。如果们又信号f(t)f(t)f(t) αk=12l∫−llf(x)e−ikπxldx,(k=0,±1,±2,...)\alpha_k=\frac{1}{2l}\int_{-l}^{l}{f(x)e^{-i \frac{k \pi x}{l}}dx}...
离散傅里叶变换的应用之实时频谱显示
wwxy1995的博客
05-06 608
dsp低通滤波器设计实验之一：傅里叶变换
weixin_30293079的博客
08-19 585
这其实是我的dsp课程的课程设计，老实说，一个学期的dsp课程并没有使我对dsp芯片增加了多少了解，更多的收获是终于知道之前看如天书的数字信号处理是用来干嘛的了，然而，这也并没有什么卵用，也丝毫没有减少我对傅里叶的恨意，哈哈，说说笑。 设计一个低通滤波器，这其实是一个很简单很简单的课程设计，甚至，还称不上课程设计，叫实验也不为过。我之所以想把它写出来，一是临近毕业，想把这...
DSP-快速傅里叶变换（FFT）
vizio.blog.youkuaiyun.com
11-19 3566
DSP-快速傅里叶变换（FFT）
数字信号处理翻转课堂笔记8——离散傅立叶变换（DFT）的应用：计算线性卷积&分析频谱
WM2101的博客
10-16 5609
DFT的应用：计算线性卷积、分析频谱
数字信号处理学习笔记（一）|离散傅里叶变换
qq_43411654的博客
08-27 9716
离散傅里叶变换（DFT） 离散傅里叶变换（Discrete Fourier Transform）的实质是有限长序列傅里叶变换的有限点离散采样，实现了频域离散化，使数字信号处理可以在频域采用数值运算的方法进行，增大了数字信号处理的灵活性。 一、DTF的定义 设x(n)是一个长度为M的有限长序列，则定义x(n)的N点离散傅里叶变化为： 二、DFT物理意义 序列x(n)的N点DFT是x(n)的Z变换在单位元上的N点等间隔采样 ...
DSP初学者学习笔记自用手写
11-01
3. **离散时间傅里叶变换（DTFT）**：DTFT是分析离散信号频谱特性的基础，它将离散时间信号转换为频率域表示，为滤波器设计和信号分析提供了理论基础。 4. **快速傅里叶变换（FFT）**：FFT是DTFT的高效算法，大大...
数字信号处理翻转课堂笔记5——z变换&离散LTI系统零极点与频率响应特性&滤波器设计初步
WM2101的博客
10-05 1万+
z变换，离散LTI系统的系统函数零极点与系统频率响应特性，滤波器设计初步
DSP操作教程 4-7 快速傅立叶变换（FFT）算法（CCS显示）
Tronlongtech的博客
09-20 4739
在计算机上进行的DFT，使用的输入值是时域的信号值，输入采样点的数量决定了转换的计算规模。FFT和FFT 逆变换函数中的第五个参数brev是指向包含64个表项的位反转表的指针，因此程序中需要提供64个表项，程序中的位反向表是计算出来的，可以通过代码提前转换的。离散傅里叶变换作为信号处理中最基本和最常用的运算，在信号处理领域占有基础性的地位，如果直接按照离散傅里叶变换的公式进行计算，求出N点X(k)需要N^2次复数运算、N(N-1)次复数加法，当N很大时，运算量是非常大的，这对于实时处理是无法接受的。
傅里叶变换
crossoverpptx的博客
09-26 6243
在计算机视觉中，有一个经典的变换被广泛使用——傅里叶变换。傅里叶变换是将时间域上的信号转变为频率域上的信号，进而进行图像去噪、图像增强等处理。
如何 FFT(快速傅里叶变换) 求幅度、频率（超详细 含推导过程）
热门推荐
Xav Pun的博客
11-30 13万+
保姆级教学➕全部代码➕原理解释➕推导过程
数学的回忆（零）——傅立叶
图像学习之旅
09-17 1473
一、什么是频域 从我们出生，我们看到的世界都以时间贯穿，股票的走势、人的身高、汽车的轨迹都会随着时间发生改变。这种以时间作为参照来观察动态世界的方法我们称其为时域分析。而我们也想当然的认为，世间万物都在随着时间不停的改变，并且永远不会静止下来。但如果我告诉你，用另一种方法来观察世界的话，你会发现世界是永恒不变的，你会不会觉得我疯了？我没有疯，这个静止的世界就叫做频域。 先举一个公式上并非很恰当...
DSP实验（二）离散傅里叶变换（DFT）
m0_46522853的博客
07-27 1644
DSP实验（二）DFT 1.DFT 的 MATLAB 仿真实验 在 MATLAB 中编写脚本，以 cos 函数建模，生成一个幅度为 5Vpp，长度为1 秒的实线性调频信号，其调频率为 400Hz/s，起始频率为 50Hz，采样点数为 1024点。 使用 FFT 函数计算其频谱，使用 fftshift 函数将其频谱搬移成按 0 左右对称。 clc;clear; T = 1; fs = 1024; f0 = 50; %信号载频 N = fs * T; t = linspace( 0,
深入理解DSP中的重要概念（FT、DTFT、DFT、DFS、ZT、FFT）
weixin_44618906的博客
05-03 1万+
这篇博客主要梳理数字信号处理领域里面比较重要的几个概念以及之间的关系，包含以下几个内容 傅里叶变换(FT) 离散时间傅里叶变换(DTFT) 离散傅里叶变换(DFT) 离散傅里叶级数(DFS) Z 变换(ZT) 快速傅里叶变换(FFT)。 1. 转换成可处理的数字信号的要求 一方面保证是离散的 (时域与频域)，另一方面保证信号是有限的 (时域与频域)。 2. 从 FT 到 DTFT 首先给出 FT 的表达式 F(jω)=∫−∞∞f(t)e−jωtdtF(j\omega) = \int_{-\infin}^
【算法】离散傅里叶变换(DFT)
Carol0630的博客
04-13 2万+
真实的系统是会离散的，时变的。理想者将瞬时态看成时线性的系统，将时变系统分成了不同阶段。离散在围观层面是连续的，但从表层感受时，变化是迅猛的，可以忽略不计变化的过程，因而成为了离散。 一、离散系统 离散控制系统是指在控制系统的一处或数处信号为脉冲序列或数码的系统。如果在系统中使用了采样开关,将连续信号转变为脉冲序列去控制系统,则称此系统为采样控制系统。如果在系统中采用了数字计算机或数字控制器,其信号是以数码形式传递的,则称此系统为数字控制系统。通常把采样控制系统和数字控制系统统称为离散控制系统。离散系统.
傅里叶变换（DFT）从原理到代码
zimujun711的博客
11-29 4229
FFT傅里叶变换相关知识
FFT—快速傅里叶变换算法——STM32F1+DSP库实现（2）
qq_27762895的博客
11-29 3万+
STM32F1 DSP官方库的安装 1.下载完毕后进行安装，这里我甩出一个下载链接。 2.接收协议。 3.安装路径，我这里喜欢选择D盘。 4.安装完毕后，有一些需要的库和参考Demo文件。 5. STM32F1移植ST 的DSP官方库 在STMF1上移植ST 的FFT官方库运行一下看一下效果，然而STM32F103毕竟不是STM32F4系列的处理器，对于一般的FFT运算...
DSP频谱分析——选取合适的N和窗函数得到6根非零谱线
wangnianrui的博客
05-18 870
题目： 假设信号x(n)=0.001*cos(0.45nπ)+sin(0.3nπ)-cos(0.302nπ-π/4). 请选择合适的长度N和窗函数，用DFT分析频谱，得到6根非零谱线。 clc;clear n=0:1:1999; x=0.001*cos(0.45*n*pi)+sin(0.3*n*pi)-cos(0.302*n*pi-pi/4); %T=1000，所以N要取1000的整数倍才能不泄露 %先确定x(n)的1000点DFT n1=0:1:999; %取1000个点 y1=x(1:1:
评论 1
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值