Stable Matching Problem

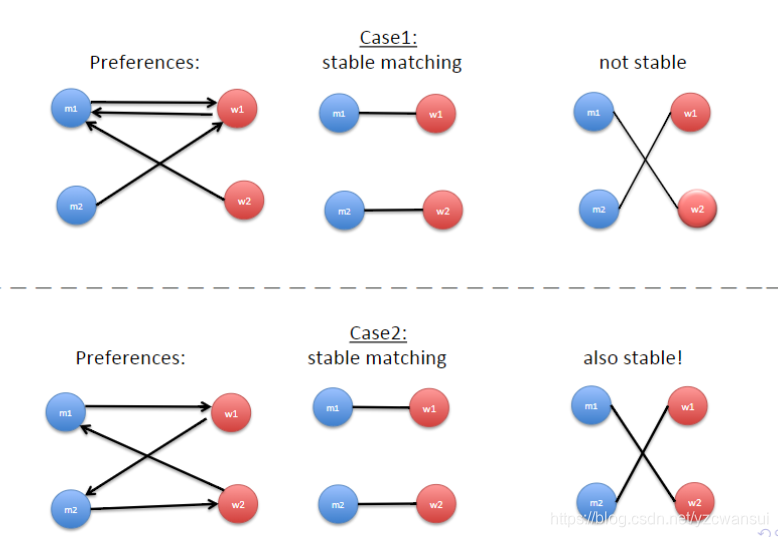
Problem

Assume that you are running a dating agency and haven men and nwomen as customers;

They all attend a dinner party; after the party

• every man gives you a list with his ranking of all women persent, and
• every woman gives you a list with her ranking of all men present

Design an algorithm which produces a stable matching:
a set of n pairs p = (m, w) of a man m and a woman w, so that the following situation never happens

for two pairs p = (n, w) and p’ = (m’, w’):

• man m prefers woman w’ to woman w
• woman w’ prefers man m to man m’

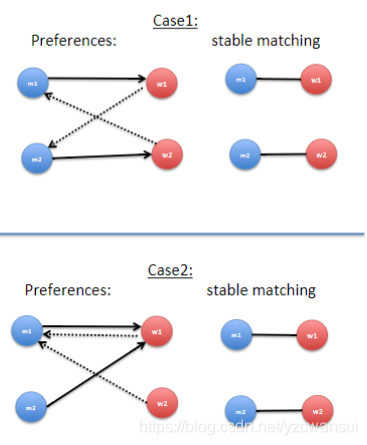
change to

Given n men and n women, There are $$n!\approx (n/e{)}^n$$more than exponentially many in n.

Therefore, it is necessary to find a stable matching algorithm in a reasonable amount of time(Gale-shapley algorithm).

Gale-Shapley algorithm

• Produces pairs in stages， with possible revisions
• A man who has not been paired with a woman will be called free.
• Men will be proposing to woman.Women willl decide if they accept a proposal or not.
• start with all men free

While (there exists a free man who has proposed to all women pick such a 
	free man m and have him propose to the highest ranking woman w on his 
	list to whom he has not proposed yet)
	if no one has sproposed to w yet
		she always accepts and a pair p = (m, w) is formed
	else she is already in a pair p' = (m', w);
		if m is higher on her perderence list than m'
			the pair p' = (m', w) is deleted
			m' becomes a free man;
			a new pair p = (m, w) is formed
		else (m is lower on her preference list than m')
			the proposal is rejected and m remains free.

• Claim 1: Algorithm terminates after $\le n^2$ rounds of the while loop
  proof:

  • In every round of while loop one man proposes to one woman
  • every man can propose to a woman at most once
  • thus every man can make at most n proposals
  • there are n men, so in total they can make $\le n^2$proposals

  Thus the while loop can be executed no more than $n^2$ many times

• Claim 2: every man is eventually paired with a woman(vice versa to woman)
  proof:

  • Assume that the while While loop has terminated, but m is still free.
  • This means that m has already proposed to every woman.
  • Thus, every woman is paired with a man, because a woman is not paired with anyone only if no one hs made a proposal to her
  • But this would mean that n women are paired with all of n men so m cannot be free.Contradiction!

• Claim 3: The matching produced by the algorithm is stable
  proof: Note that during the While loop:

  • a woman is paired with men of increasing ranks on her list.
  • a man is paired with women of decreasing ranks on his list.

  Assume now the opposite, that the matching is not stable; thus, there are two pairs p = (m, w) and p’ = (m’, w’) such that:

  • Since m prefers w’ over w, he must have proposed to w’ before proposing to w;

  • Since he is paired with w, woman w’ must have either:

    • rejected him because she was alread with someone whom she prefers ot
    • dropped him later after a proposal from someone whom she prefers

  • In both cases she would now be with m’ whom she prefers over m.

  • Contradiction