隐私保护——差分隐私

差分隐私

参考书籍：

《隐私计算》 - 陈凯, 杨强

《深入浅出隐私计算》 - 李伟荣

结合大模型工具，以此笔记，记录自己的学习过程。

前置知识

1.什么是隐私？

在生活中，大家会觉的只要是包括自身数据的数据暴露，就全部是隐私泄露，但从隐私保护的专业角度讲，隐私的主体是单个用户，只有牵涉到某个特定用户才属于隐私泄露，而群体用户的信息（聚集信息）的发布不属于隐私泄露范畴。

例如，如果医院发布了一个用于证明肺癌和吸烟相关性的数据集，并且这个数据集已经经过了适当的匿名化处理，并且没有足够的信息可以重新识别个体，那么这通常不被视为侵犯隐私，但如果医院让别人知道某个具体病人（如 Alice）是否患有肺癌以及是否吸烟，这就是侵犯了隐私。

简而言之，就是只要不要让人知道数据是谁的数据，就不算数据泄露，隐私就依旧被保护的很好。

2.什么是邻近数据库

邻近数据库是指两个仅相差一个记录的数据库。

具体来说，如果数据库$D_1$ 和 $D_2$ 满足以下条件之一，则称它们为邻近数据库：

• $D_1$ 可以通过在 $D_2$ 中添加一个记录得到。
• $D_1$ 可以通过在 $D_2$ 中删除一个记录得到。
• $D_1$ 可以通过在 $D_2$ 中替换一个记录得到。

例如，Alice来医院检查后，医院的证明肺癌和吸烟相关性的数据库里多了一条数据，这个时间点前后的数据库就是邻近数据库。

同理，邻近数据集也是一样的。

核心知识

1.什么是差分攻击？

差分攻击的核心思想是通过比较系统在不同输入下的输出差异，来推断出关于输入的敏感信息。

差分攻击通常包括以下几个步骤：

1. 构造输入：攻击者构造两个相邻的数据库$D$和$D^{\prime }$（即仅相差一个记录的数据库），这两个数据库仅相差一个记录。
2. 获取输出：攻击者分别对这两个数据库执行相同的查询操作，获取查询结果$f(D)$和$f(D^{\prime })$。
3. 比较输出：攻击者比较 结果$f(D)$和$f(D^{\prime })$的差异，分析这些差异以推断出关于缺失记录的信息。

例如：攻击者对上面提到的肺癌和吸烟相关性数据集精心构造了两个具有100条数据的邻近数据库（例如攻击者知道Alice的看病时间，得到这个时间点的前后数据库的内容）。对数据库$D$查询这个数据集种患者患有肺癌的人数，发现为12个患者，对数据库$D^{\prime }$数据库查询，发现有13个患者，那么攻击者就可以知道Alice患了病。这就是差分攻击。

2.灵敏度

在差分隐私中，灵敏度（Sensitivity）用于衡量查询函数在邻近数据集之间的最大差异。灵敏度的定义和计算方法取决于函数的性质。

对于一个查询函数 $f$，其灵敏度 $\Delta f$定义为：

$$\Delta f=\underset{D_1,D_2\text{ are adjacent}}{\max }\Vert f(D_1)-f(D_2)\Vert$$

这里，$D_1$和 $D_2$ 是邻近数据集，$\Vert \cdot \Vert$ 表示某种范数（通常是 $L_1$范数或$L_2$范数）。

假设我们有l两个数据集，$D_1$ 包含 1000 名患者，其中 120 名患有肺癌。$D_2$ 包含 999 名患者，其中 119 名患有肺癌（假设 Alice 患有肺癌）。而灵敏度实际上应该是单个记录对查询结果的最大影响。对于计数查询这个查询函数：查询函数 $f(D)$ 返回数据集中患有肺癌的患者数量。灵敏度 $\Delta f=1$，(因为添加或删除一个记录最多改变计数 1)。针对比例查询这种查询函数$f(D)$返回数据集中患有肺癌的患者比例，查询结果$f(D)=\frac{120}{1000}=0.12$,$f(D^{\prime })=\frac{119}{999}\approx 0.1191$则灵敏度为$\Delta f=\left|0.12-0.1191\right|=0.0009$

3. 差分隐私的核心理念是什么？

差分隐私直白来说，就是构造一种算法，让攻击者在获取两个相邻的数据集$D$和$D^{\prime }$之后，用同一个查询方式获取的查询结果$R$和$R^{\prime }$非常接近（小于灵敏度），这样攻击者就无法通过比较获取查询结果$R$和$R^{\prime }$的差异获取具体的信息。

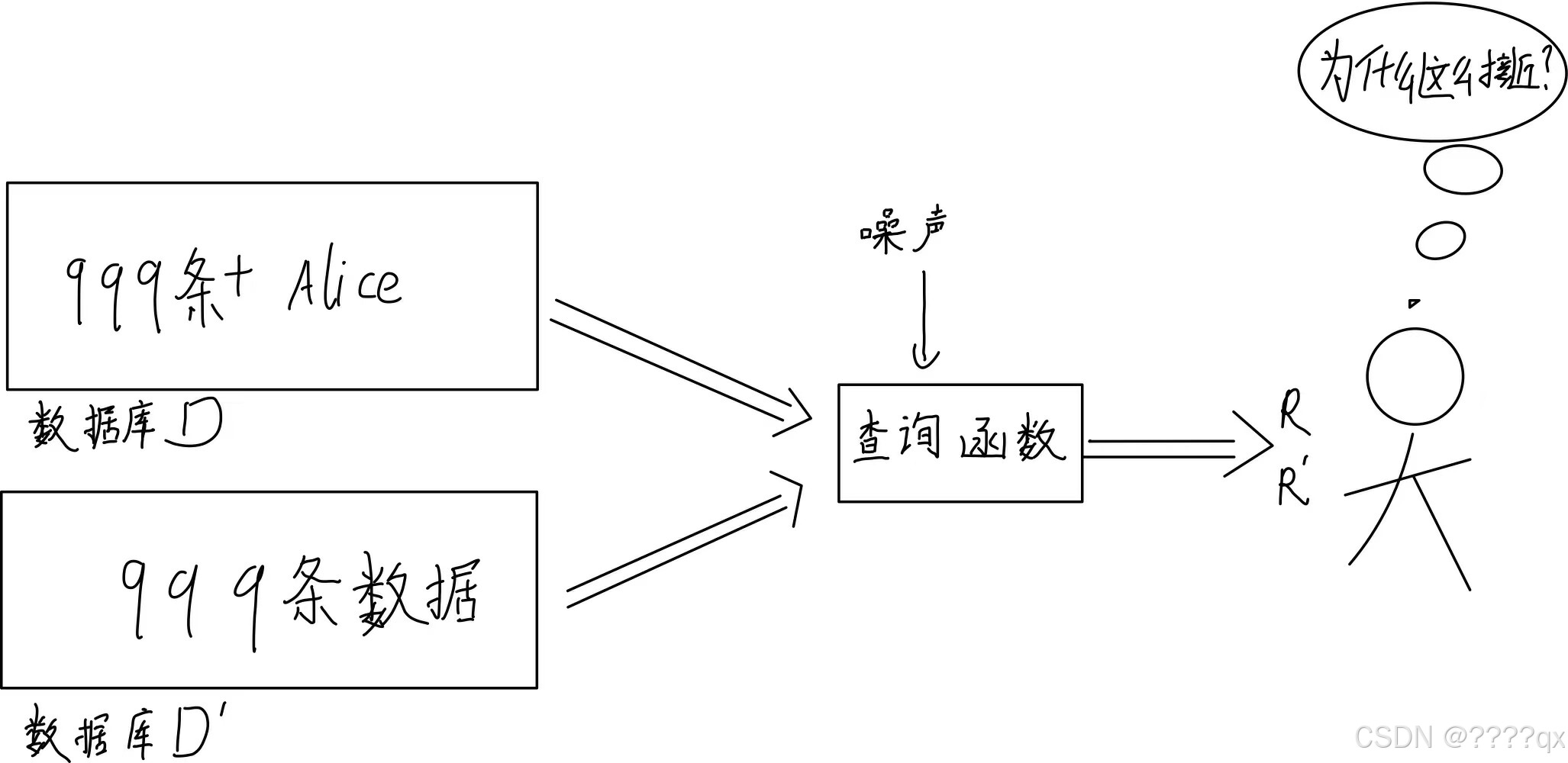
例如：如图所示，Alice检查后的数据库$D$包含 1000 名患者，其中 120 名患有肺癌。Alice检查前$D^{\prime }$包含有999名患者， 其中 119 名患有肺癌（假设 Alice 患有肺癌）。这两个数据库就是攻击者也是探查Alice是否患病的攻击者会获取的一对邻近数据库$D$和$D^{\prime }$。看之前的案例就可以知道，原本Alice检查后的数据库$D$查询结果为0.121。Alice检查前$D^{\prime }$的查询结果0.1191。但是现医院设计了一种算法，让攻击者对数据库$D$和$D^{\prime }$分别查询患肺癌的概率时，的查询结果为：让Alice检查后的数据库$D$查询结果为0.119，Alice检查前$D^{\prime }$的查询结果0.1206。这个结果在Alice检查后，患癌概率甚至发生了下降。（本例子中为了让变化更加明显，让查询结果不升反降，但是在差分隐私下邻近数据库的查询结果只会具有差距小于灵敏度这个特征，不一定是不升反降，也可能升高）

当攻击者在构造出邻近数据库后，使用同样的两个结果的差距过于微小，并不符合一个邻近数据集的数据发生的变动的差异后的变化，这就让攻击者摸不着头脑，无法得到Alice患病信息。但是由于这两个结果本身又非常的接近，单独使用任何一个结果都不妨碍研究者研究这个数据集得出关于患癌症和抽烟的关系。

差分隐私的分类方式

一.根据参数的分类方式

1. 差分隐私的根据参数的分类方式有哪些？

差分隐私一般包括如下两种形式：

• ε-差分隐私：这是一种严格的隐私保护形式，令相邻的数据库 $D_1$ 和$D_2$，使用添加了随机扰动的查询机制$\mathcal{M}$，得到算法以及所有可能的输出集合 $S$，都有：
  $$\frac{\mathrm{Pr}[\mathcal{M}(D_1)\in Y]}{\mathrm{Pr}[\mathcal{M}(D_2)\in Y]}\le e^{\epsilon }$$
  进一步，得到变式如下
  $$\mathrm{Pr}[\mathcal{M}(D_1)\in Y]\le e^{\epsilon }\cdot \mathrm{Pr}[\mathcal{M}(D_2)\in Y]$$

  $\epsilon$ 表示隐私保护的强度。较小的$\epsilon$值意味着更强的隐私保护。查询结果在邻近数据库之间的概率比不会超过 $e^{\epsilon }$。

• (ε, δ)-差分隐私：这是一种稍微宽松的隐私保护形式，允许有一定的失败概率$\delta$。具体来说，要求对于所有相邻的数据库 $D_1$ 和 $D_2$，以及所有可能的输出集合$S$，都有：

  $$\mathrm{Pr}[\mathcal{M}(D_1)\in Y]\le e^{\epsilon }\cdot \mathrm{Pr}[\mathcal{M}(D_2)\in Y]+\delta$$

  $\delta$ 表示差分隐私保护失败的概率。具体来说，$\delta$是一个很小的正数。

2.参数$\epsilon$是什么？

$\epsilon$ 是一个正实数，表示隐私保护的强度。较小的$\epsilon$值意味着更强的隐私保护，但可能会降低数据的可用性。较大的$\epsilon$值意味着较弱的隐私保护，但可能会提高数据的可用性。

其中，当$\epsilon$=0的时候，显然有$\mathrm{Pr}[\mathcal{M}(D_1)\in Y]/\mathrm{Pr}[\mathcal{M}(D_2)\in Y]=1$，也就是说任意两个相邻的数据集他们的输出有完全相同的分布（也就是相同的输出结果）。这使得隐私保护变为最强，但是为了完成这种无论输入数据集是什么都不会改变输出结果，算法$\mathcal{M}$也会退化为均一算法（均一算法的意思就是无论输入的数据集是什么，算法的输出分布都是相同的）。也就是说，此时的强隐私保护是以牺牲数据效用为代价的。由于输出结果都是相同的，这个结果本身不能用于任何有意义的分析或推断。

例如，假设我们有一个相邻数据集是$D_1$还是$D_2$，包含 1000 名患者的是否吸烟和是否患有肺癌的信息。我们使用一个满足$\epsilon =0$的差分隐私算法$\mathcal{M}$来计算数据集中患有肺癌的患者比例。由于$\epsilon =0$，无论输入的数据集是$D_1$还是$D_2$，算法的输出分布都是相同的，完全随机的，输出结果可能是任何随机值，例如 0.15、0.20、0.10 等，与实际的患者比例无关，这样的输出结果虽然完全瞒过了攻击者，但是对于正常研究者来说，这样的数据也没有任何意义。

选择$\epsilon$的注意事项

1. $\epsilon$应该适当选择：

   • $\epsilon$的选择需要根据具体应用场景和隐私保护的需求来确定。通常，$\epsilon$会在 0.1 到 1 之间选择，但这并不是固定的标准，需要根据实际情况调整。

2. $\epsilon$与数据效用的权衡：

   • 较小的$\epsilon$值会增加查询结果中的噪声，从而降低数据的效用。因此，需要在隐私保护和数据效用之间找到一个平衡点。

• 例如，对于高度敏感的数据（如医疗记录），可以选择较小的$\epsilon$值；对于不太敏感的数据，可以选择较大的$\epsilon$值。

3. $\epsilon$的累积效应：

   • 在多次查询或多次应用差分隐私机制时，$\epsilon$的累积效应需要特别注意。使用组合定理可以管理多次查询的隐私预算，确保总的隐私保护水平。

   • 例如，如果一个算法在 k 次独立执行中每次满足${\epsilon }_i$-差分隐私，那么总的结果满足$\epsilon$-差分隐私，其中：

$$\epsilon =\sum _{i=1}^k{\epsilon }_i$$

3.参数$\delta$是什么？

在$(\epsilon ,\delta )$-差分隐私（Approximate Differential Privacy）中的$\delta$表示差分隐私保护失败的概率。具体来说，δ 是一个很小的正数。也就是说，与$\epsilon$-差分隐私相比，$(\epsilon ,\delta )$-差分隐私允许一定的概率失败。这个是因为严格的$\epsilon$-差分隐私（即$\delta =0$）可能需要添加大量的噪声来确保隐私保护，尤其是在高维度数据集和多次查询的过程中，这些噪声会显著降低数据的可用性和效用。通过引入$\delta$，可以在一定程度上减少所需添加的噪声量，从而提高数据的效用。($\epsilon ,\delta$)-差分隐私提供了一种更灵活的方式来平衡隐私保护和数据效用。通过调整$\epsilon$和$\delta$的值，可以找到一个合适的点，使得数据既具有足够的隐私保护，又具有较高的实用性。

选择$\delta$的注意事项

1. $\delta$应该非常小：

   • 选择过大的$\delta$会增加隐私泄露的风险，使得差分隐私保护的效果大打折扣。$\delta$应该选择得非常小，以确保隐私保护的可靠性。通常，$\delta$会取一个非常小的值，例如$10^{-6}$或$10^{-8}$。

2. $\delta$与$\epsilon$的平衡：

   • $\delta$和$\epsilon$之间存在权衡。较小的$\delta$通常需要较大的$\epsilon$，反之亦然。在实际应用中，需要根据具体需求和风险容忍度来选择合适的$\epsilon$和$\delta$。

3. $\delta$的累积效应：

   • 在多次查询或多次应用差分隐私机制时，$\delta$的累积效应需要特别注意。使用高级组合定理可以管理多次查询的隐私预算，确保总的隐私保护水平。

二.根据噪声类型的分类方式/经典算法

1.离散值域：随机回答

（1）什么是随机回答？

随机回答（Randomized Response, RR）通过引入随机性来掩盖个体的真实响应，从而保护受访者的隐私。具体来说，受访者在回答敏感问题时，以一定的概率提供真实答案，以另一概率提供随机答案。

随机回答（Randomized Response, RR）通过引入随机性来掩盖个体的真实响应，从而保护受访者的隐私。具体来说，受访者在回答敏感问题时，以一定的概率提供真实答案，以另一概率提供随机答案。

假设有一个敏感问题，例如受访者是否吸烟的问题，答案只有“是”或“否”。

步骤：

• 受访者投掷一枚不公平硬币，正面出现的概率为$p$（例如$p=0.5$），反面出现的概率为$1-p$。
• 如果硬币正面朝上，受访者回答真实答案。
• 如果硬币反面朝上，受访者随机选择一个答案（例如，“是”或“否”）。

通过这种方式就给数据加入了噪声。同理，这个模型可以扩展到多选项问题里。

（2）差分隐私与随即回答的结合

随机回答和差分隐私结合使用，以提供更强大的隐私保护。以下是几种常见的结合方式：

1. 局部差分隐私（Local Differential Privacy, LDP）中的随机回答：

   • 在每个用户的设备上应用随机回答技术，然后将扰动后的数据发送到中心服务器进行聚合分析。

2. 中央差分隐私（Central Differential Privacy, CDP）中的随机回答：

   • 在中央服务器上收集原始数据后，先应用随机回答技术对数据进行预处理，然后再应用差分隐私技术。

3. 混合方法：

   • 在某些情况下，可以先应用随机回答技术，然后再应用差分隐私技术。例如，在调查中，受访者首先使用随机回答提供答案，然后在中央服务器上对这些答案应用差分隐私技术进行进一步处理。

2.连续值域：拉普拉斯噪声法

（1）拉普拉斯分布

拉普拉斯分布的概率密度函数为：
$$f(x;b)=\frac{1}{2b}\exp \left(-\frac{|x|}{b}\right)$$

其中$b$是尺度参数，决定了噪声的大小,拉普拉斯分布通常是表示为$x\sim Lap(b)$。

（2）拉普拉斯噪声法

差分隐私的拉普拉斯噪声法定义为

$$A_L(D,f,\epsilon )=f(x)+\left(Y_1,\cdots ,Y_k\right)$$
式中，$Y_i$是属于服从$Lap({\Delta }_{1}f/\epsilon )$的随机变量.

拉普拉斯机制是一种常用的实现$\epsilon$-差分隐私的方法。其基本步骤如下：

例如，假设我们有一个数据集$D$，包含 1000 名患者，其中 120 名患有肺癌。我们希望发布患有肺癌的患者数量，并使用拉普拉斯机制来保护隐私。

1. 计算灵敏度：确定查询函数$f$的灵敏度$ \Delta f$，即邻近数据库之间的最大差异。
   • 查询函数结果$f(D)=120$（患有肺癌的患者数量）。
   • 灵敏度$\Delta f=1$，因为添加或删除一个记录最多改变计数 1。
2. 添加噪声：在查询结果$f(D)$ 上添加拉普拉斯噪声 $\text{Lap}(\Delta f/\epsilon )$
   • 选择$\epsilon =1$，$\Delta f/\epsilon =1$
   • 从拉普拉斯分布$\text{Lap}(1)$中采样一个噪声值$N$。假设采样的噪声值$N=0.5$。
3. **输出结果：**最终的输出为 $f(D)+N$
   • 即输出后的结果为$120+0.5=120.5$。

（3）对拉普拉斯噪声法的验证

证明拉普拉斯噪声法满足 ε-差分隐私。

证明：令 $D_1, D_2 $为相邻数据集，令 $p_1,p_2$ 分别为 $A_L(D_1,f,\epsilon ),A_L(D_2,f,\epsilon )$的概率密度函数，考虑其在任意 $z\in {\mathbb{R}}^k$ 的概率密度：

$$\begin{array}{rl}& \frac{P_1(z)}{P_2(z)}\\ =& \prod _{i=1}^k\left(\frac{\exp \left(-\frac{\epsilon |f(D_1{)}_i-z_i|}{\Delta f}\right)}{\exp \left(-\frac{\epsilon |f(D_2{)}_i-z_i|}{\Delta f}\right)}\right)\\ =& \prod _{i=1}^k\exp \left(\frac{\epsilon \left(|f(D_2{)}_i-z_i|-|f(D_1{)}_i-z_i|\right)}{\Delta f}\right)\\ ⩽& \prod _{i=1}^k\exp \left(\frac{\epsilon |f(D_1{)}_i-f(D_2{)}_i|}{\Delta f}\right)\\ ⩽& \exp (\epsilon ),\end{array}$$

式中，第一个不等号是因为三角不等式，第二个不等号是依据差分隐私定义，定理得证。

3.连续值域：高斯噪声法

(1）高斯分布

高斯分布的概率密度函数为：
$$f(x;\mu ,{\sigma }^2)=\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left(-\frac{(x-\mu {)}^2}{2{\sigma }^2}\right)$$

其中$\mu$是均值，${\sigma }^2$是方差。通常是表示为$x\sim \mathcal{N}(b)$。

（2）高斯噪声法

差分隐私的高斯噪声法定义为

$${\mathcal{A}}_N(D,f,\sigma )=f(D)+(Y_1,\cdots ,Y_k)$$
式中，$Y_i$是属于服从$\mathcal{N}(0,{\sigma }^2)$的随机变量.

高斯机制是一种常用的实现满足$(\epsilon ,\delta )$-差分隐私的方法。其基本步骤如下：

例如，假设我们有一个数据集$D$，包含 1000 名患者，其中 120 名患有肺癌。我们希望发布患有肺癌的患者数量，并使用高斯机制来保护隐私。

1. 计算灵敏度：确定查询函数$f$结果和灵敏度$ \Delta f$，即邻近数据库之间的最大差异。

   • 查询函数结果$f(D)=120$（患有肺癌的患者数量）。
   • 灵敏度$\Delta f=1$，因为添加或删除一个记录最多改变计数 1。

2. 添加噪声：选择合适的$\epsilon$和$\delta$值。通常$\delta$是一个非常小的正数（例如 10^{-5} 或 10^{-6}），表示允许一定的失败概率。在查询结果$f(D)$ 上添加高斯噪声 $\sigma \ge \frac{\Delta f}{\epsilon }\sqrt{2\ln (1.25/\delta )}$

   • 选择$\epsilon =1$和$\delta =10^{-5}$。

   • 根据公式计算噪声尺度$\sigma$：

     $$\sigma \ge \frac{1}{1}\sqrt{2\ln (1.25/10^{-5})}\approx \sqrt{2\ln (125000)}\approx \sqrt{2\times 11.73}\approx \sqrt{23.46}\approx 4.84$$

   • 从高斯分布$\mathcal{N}(0,{\sigma }^2)$中采样一个噪声值，此例子中我们假设取得的N为0.13

3. **输出结果：**最终的输出为 $f(D)+N$

   • 扰动后的结果为 120 + 0.13。

（3）对高斯噪声法的验证

令$\epsilon \in (0,1)$。若$c^2>2\ln (1.25/\delta )$，则当$\sigma >c{\Delta }_{2}f/\epsilon$时，$(\epsilon ,\delta )$-差分隐私的定义成立。

三 . 其他分类方式

1.根据原始数据存储位置的分类方式

中心化差分隐私（Central Differential Privacy, CDP）

• 定义：在中央服务器上对数据进行处理，并在处理过程中添加噪声以实现差分隐私。

• 特点：适用于集中式数据收集和处理场景，如大型数据中心、云计算平台等。

• 示例：谷歌的RAPPOR系统用于收集用户浏览器设置的数据。

  

本地化差分隐私（Local Differential Privacy, LDP）

• 定义：在每个用户的设备上对数据进行扰动，然后将扰动后的数据发送到中心服务器进行聚合分析。
• 特点：适用于分布式数据收集和处理场景，确保用户数据在传输过程中得到保护。
• 示例：苹果公司在iOS中使用LDP来收集用户行为数据，如键盘输入习惯等。
• 

2.根据实现环境交互方式的分类方式

交互式差分隐私

• 定义：用户与系统进行多轮交互，每次交互时系统返回一个满足差分隐私的结果。

• 特点：适用于需要多次查询的场景，可以通过组合定理管理隐私预算。

• 示例：在线数据分析系统，用户可以多次提交查询请求。

  

非交互式差分隐私

• 定义：系统一次性发布一组满足差分隐私的数据或统计结果，用户不再与系统进行进一步交互。

• 特点：适用于一次性发布的场景，如公开数据集的发布。

• 示例：美国人口普查局发布的统计数据。

差分隐私的性质

1. 后处理

如果一个算法满足差分隐私，并且我们对这个算法的输出进行任意形式的后续处理，那么结果仍然保持原有的差分隐私保证。这意味着，即使在发布数据之后，无论攻击者如何处理这些数据，都无法从处理后的结果中获取比原始差分隐私机制所允许的更多的信息。

假设有一个算法$M$满足$\epsilon$-差分隐私或$(\epsilon ,\delta )$-差分隐私。如果我们将$M$的输出通过另一个任意确定性或随机函数$f$进行处理，得到新的输出$f(M(D))$，那么$f(M(D))$也满足与$M$相同的$\epsilon$-差分隐私或$(\epsilon ,\delta )$-差分隐私。

2. 组合性

• 序列组合：

  • 定义：如果一个系统由多个独立的$\epsilon$-差分隐私机制按顺序执行，那么整个系统的隐私损失是这些机制隐私损失的总和。
  • 公式：
    • 对于$k$个$\epsilon$-差分隐私机制，总的隐私损失为${\epsilon }_{\text{total}}=k\epsilon$。
    • 对于$k$个$(\epsilon ,\delta )$-差分隐私机制，总的隐私损失为$(k\epsilon ,k\delta )$。

• 并行组合：

  • 定义：如果多个差分隐私机制是并行执行的，并且每个机制处理的是数据集的不同部分（即数据集之间没有重叠），那么整体的隐私损失不会增加。
  • 公式：
    • 如果$k$个$\epsilon$-差分隐私机制是并行执行的，那么整体隐私损失仍然满足$\epsilon$。
    • 如果$k$个$(\epsilon ,\delta )$-差分隐私机制是并行执行的，那么整体的隐私损失仍然满足$(\epsilon ,\delta )$。

• 高级组合：

  • 定义：高级组合定理提供了一种更精确的方法来估计多次查询的隐私损失，特别是当$\delta >0$时。它通过引入额外的参数${\delta }^{\prime }$来控制失败概率，从而提供更严格的隐私损失上界。

  • 公式：

    • 对于$k$个$(\epsilon ,\delta )$-差分隐私机制，总隐私损失为$({\epsilon }^{\prime },k\delta +{\delta }^{\prime })$，其中

      $${\epsilon }^{\prime }=\sqrt{2k\ln (1/{\delta }^{\prime })}\cdot \epsilon +k\epsilon (e^{\epsilon }-1)$$

    • 这里${\delta }^{\prime }$是一个额外的小正数，用于控制失败概率。

3. 隐私预算管理

• 在实践中，可以通过分配隐私预算来控制隐私损失。例如，在一系列查询中，可以将总隐私预算分配给每一个单独的查询，以确保总体隐私保护水平。(本质是利用了差分隐私的组合性，在设置公式的时候反过来管理隐私预算)

  在多次查询中管理隐私预算的方法包括：

  • 基本组合定理：如果进行了 k 次查询，每次查询的隐私预算为 ${\epsilon }_i$，则总隐私预算为 ${\sum }_{i=1}^k{\epsilon }_i$。
  • 高级组合定理：如果进行了 k 次查询，每次查询的隐私预算为 $({\epsilon }_i,{\delta }_i)$，则总隐私预算可以通过高级组合定理进行计算，通常表达为$ (\varepsilon, \delta)$，其中$\varepsilon$ 和$\delta$ 与各次查询的参数有关。
    • 在管理高级组合的隐私预算时

4. 鲁棒性

• 差分隐私对于数据中的小变化非常鲁棒。即使攻击者拥有大量的背景知识，差分隐私也能提供有效的保护。

5. 不可逆性

• 一旦数据被差分隐私机制处理过，就不可能从发布的统计数据中恢复原始数据。这保证了数据主体的信息不会被暴露。