强化学习基础概念

1. 强化学习的概念

1 .1 基本概念

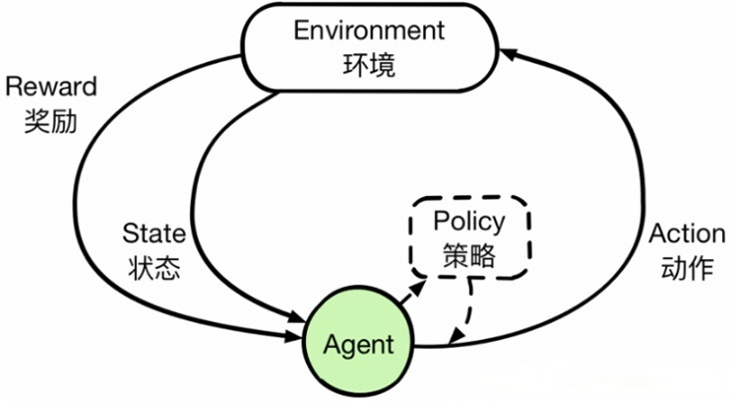
1. Agent 与 Environment（智能体与环境） 强化学习中，“智能体（Agent）”在“环境（Environment）”中感知状态、执行动作并获取奖励。 -Agent：学习决策或策略（Policy）的主体，如机器人、游戏中的AI角色。 -Environment：Agent 所处的外部世界，如迷宫、游戏环境、大自然等。
2. 状态（State） 用于描述环境在某个时刻的观察/信息。Agent 在每一个离散的时间步（Time Step）感知到一个状态。
3. 动作（Action） Agent 在给定状态下可以执行的操作（如移动、跳跃、购买股票）。执行动作后，环境会更新到新的状态。
4. 奖励（Reward） 环境对 Agent 的动作的反馈，是一个标量值，用于衡量该动作的好坏程度。Agent 的目标是让长期累积奖励最大化。
5. 回报（Return） 通常指从某一时刻开始，Agent 累积获得的折扣奖励之和（discounted sum of rewards），记为
   $$G_t=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+\dots$$
   其中$\gamma$是折扣因子（Discount Factor），取值 0～1，用于平衡“近期奖励”与“远期奖励”之间的重要性。
6. 策略（Policy） 策略$\pi$定义在给定状态时，Agent 选择动作的概率分布（或确定性函数）。策略可以是“状态→动作”的一个映射，也可以是一条决策规则。
7. 价值函数（Value Function） 用于衡量在某一状态或者“状态-动作对”上的长远收益。
   • 状态价值函数$V^{\pi }(s)$：遵循策略$\pi$时，从状态$s$开始期望得到的折扣总回报。
   • 动作价值函数$Q^{\pi }(s,a)$：遵循策略$\pi$时，从状态$s$执行动作$a$后期望得到的折扣总回报。

1.2 马尔可夫决策过程（MDP）

马尔可夫决策过程（MDP）**通常用来作为“环境”的数学建模方式，因此可以把它看作是强化学习的理论基础或框架
一个马尔可夫决策过程（Markov Decision Process, MDP）通常由如下 5 元组定义：
$$⟨S,A,P,R,\gamma ⟩$$

• $S$：状态空间（State Space），包含所有可能的状态 $s$。
• $A$：动作空间（Action Space），包含所有可能的动作 $a$。对于不同状态，也可以有不同的可执行动作集合 $A(s)$。
• $P$：状态转移概率函数 $P(s^{\prime }|s,a)$，表示从状态 $s$ 执行动作 $a$ 后转移到下一个状态 $s^{\prime }$ 的概率。
• $R$：奖励函数 $R(s,a,s^{\prime })$，执行动作 $a$ 从 $s$ 转移到 $s^{\prime }$ 后获得的即时奖励（可能也可简单写成 $R(s)$ 或 $R(s,a)$，依据具体定义）。
• $\gamma$：折扣因子（Discount Factor），用于平衡当前奖励和未来奖励的重要程度，取值通常在 [0, 1] 之间。

“马尔可夫”指的是系统在下一时刻的状态只与当前状态和动作有关，而与更早的历史无直接关系——也就是说，满足马尔可夫性质：
$$P(s_{t+1}\mid s_t,a_t,s_{t-1},a_{t-1},\dots )=P(s_{t+1}\mid s_t,a_t)$$

Agent 在每个时间步 $t$：

1. 观察当前状态 $s_t$。
2. 根据策略（Policy）$\pi$ 选择一个动作 $a_t$。
3. 执行动作，环境给出奖励 $r_{t+1}$，并转移到下一个状态 $s_{t+1}$。
4. 重复上述过程，直到达到终止状态（或无限长）。

2. 主要流派与方法

1. 基于价值（Value-based）

想象一下你玩一个迷宫游戏，你在每个位置（状态）都要做出“向哪儿走”的决定。为了做决定，你可能会估计“如果我现在走到这个方向，未来总体收益会是多少？” 这个“未来总体收益”就相当于价值。

• 核心思路：
  先学会给每个“（状态，动作）组合”打分，即“在这个状态下做这个动作，未来能收获多大好处？”。这个打分表就是所谓的 Q 函数。当我们更新完这张“打分表”后，在实际决策时就选分数最高的动作。

• 常见算法：

  • Q-Learning：经典的离线更新算法，直接更新“当前Q值”朝“即时奖励 + 下一状态的最大Q值”方向逼近。
  • Deep Q-Network (DQN)：在状态或动作特别多时，用神经网络来近似 Q 值，解决“大表格装不下”的问题。
  • 其他变体：Double DQN、Dueling DQN、Rainbow DQN 等，都在 DQN 基础上加了各种改进。

• 生活类比：

  • 假设你在选大学专业（状态），想知道“选专业A后有多少就业前景和未来发展”（价值）。
  • 你没有直接的策略（“我该怎么学习”），但你会估算“不同专业带给我的总收益是多少”，接着你就选一个价值最高的专业。

2. 基于策略（Policy-based）

如果把基于价值的做法比作“先给每个选项打分，再挑分数最高的选项”，那么基于策略就是“干脆直接学一套选项的生成规则，如何直接给出动作”。不用先生成一个Q值或价值表格，而是把“选动作”的过程封装成一个带参数的模型，参数变化就会改变行动偏好。

• 核心思路：
  直接让策略（Policy）去决定每个状态下的“动作选择概率”。比如在状态 ss 下，“往上走”的概率 0.3，“往右走”的概率 0.5，“往下走”的概率 0.2。然后我们根据这些概率去玩游戏、收集分数，再通过梯度下降（或其它优化手段）去调整这个策略，让它逐渐倾向于更容易拿高分的动作。

• 常见算法：

  • REINFORCE：最基础的策略梯度方法，原理相对简单，但数据效率和稳定性略低。
  • Actor-Critic：把“决策者（Actor）”和“评价者（Critic）”分开，前者输出动作概率，后者估计价值，用来帮助减小梯度训练的方差。
  • PPO (Proximal Policy Optimization)：一个在工程中常用的改进方法，通过限制新旧策略差异，让训练更稳定，不会“翻车”太厉害。

• 生活类比：

  • 你学弹钢琴，不会先估算每个音符带来的“价值”。而是边弹边练，让大脑直接形成“如何指法与节奏分配”的整体模式。
  • 训练过程就是不断根据“表演结果”来调整大脑中的连接，让后续弹奏越来越好。

3. 基于模型（Model-based）

前面两种方法都不去显式地学习“环境内部的转移规律”，而是直接（或间接）学习价值或策略。但有些时候，我们可能希望先构建一个“环境模型”，类似“在状态s执行动作a后，大概率会转移到哪个状态、得多少奖励”，然后在自己的模型里做计划或搜索。这就是基于模型的方法。

• 核心思路：

  1. 学习或已经知道环境转移、奖励的过程（比如写在一个物理仿真器里、或用神经网络去拟合）；
  2. 在这个模型里模拟各种可能的路径，评估收益；
  3. 通过搜索或规划（例如蒙特卡洛树搜索MCTS）找到最优决策。

• 常见场景：

  • AlphaGo/AlphaZero：它先学习一个神经网络来预测下一步局面和胜率（也相当于“环境模型+价值估计”），再用蒙特卡洛树搜索在这个模型里进行大量模拟，得出最好的下一手棋。
  • 机器人控制：如果有比较精确的物理模型，就可以在模拟器里做大量试验，减少在现实中摔坏的风险。

• 优缺点：

  • 优点：能利用规划或搜索，通常学习速度快、数据利用率高；对复杂的长序列决策也更灵活。
  • 缺点：需要精确或可学到的“环境模型”，对环境复杂度和运算量要求较高。

• 生活类比：

  • 你打算环游世界，就先用地图和攻略模拟每个地点之间的交通、可能花费和风险，再计划出一条最佳路线，而不是直接“每到一处再随机走”。
  • 不过如果地图不准，或你完全没有地图，你只能走到哪算哪（那就回到 value-based 或 policy-based 的思路）。

不同流派各有用途和优势，实际应用中也常常把它们结合起来，比如同时估值、学策略、用环境模型做规划等，形成“混合式”方法，取得更高的效率或更好的效果。

3. 强化学习的核心算法

3.1 Q-Learning 系列

• Q-Learning：基于价值函数的离线更新方法，通过更新公式（Bellman方程）迭代逼近最优$Q^{\ast }(s,a)$。 简单说核心思路是当前状态-动作的 Q 值更新得更加接近“即时奖励 + 下一个状态的最优 Q 值”。
  $$Q(s,a)\leftarrow Q(s,a)+\alpha (R+\gamma \underset{a^{\prime }}{\max }Q(s^{\prime },a^{\prime })-Q(s,a))$$

• Deep Q-Network (DQN)：使用神经网络近似 Q 函数，引入经验回放（Experience Replay）和目标网络（Target Network）以提高训练稳定性。

3.2 策略梯度（Policy Gradient, PG）系列

• REINFORCE：直接对策略${\pi }_{\theta }(a|s)$的参数$\theta$求梯度，通过增大在回报高的轨迹中出现动作的概率，使得策略更倾向于产生高回报。
• Actor-Critic：结合了价值函数和策略梯度的思想，Actor 负责输出动作的概率分布，Critic 负责估计动作价值或状态价值，以降低高方差、稳定训练。
• PPO (Proximal Policy Optimization)：在更新策略时限制新旧策略之间的变化幅度，兼顾收敛速度和策略更新的稳定性。

3.3 AlphaGo/AlphaZero 类模型

• 利用自对弈（Self-Play）收集数据，结合蒙特卡洛树搜索（MCTS）和神经网络，对策略和价值函数进行联合训练，可用于复杂博弈任务（如围棋、国际象棋、将棋）。

4. 强化学习中的关键技巧与挑战

1. 探索与利用（Exploration vs. Exploitation）

   • 面临随机或未知环境时，Agent 既要探索新的动作与策略，又要利用当前学到的最优决策。
   • 常见做法：$ϵ$-贪心策略（$ϵ$-Greedy）、UCB、Boltzmann Exploration 等。

2. 稳定性与收敛速度

   • 深度强化学习通常不如监督学习稳定，容易陷入局部最优或不收敛。
   • 需要通过经验回放、目标网络、归一化奖励等技巧来提高训练稳定性。

3. 样本效率

   • RL 往往需要大量的交互数据，一些真实应用（如机器人控制）可能难以长时间试错。
   • 解决方案包括仿真环境、模型学习、层次化RL等。

4. 多智能体（Multi-Agent RL）

   • 多个 Agent 在同一个或互相影响的环境中学习，需要考虑博弈、合作或竞争关系。

5. 安全与可解释性

   • 部分场景（如自动驾驶、医疗决策）对安全性要求很高，需要在收敛前避免灾难性动作。
   • RL 的可解释性也相对较难，需要更多研究或可视化技术。

5. 深度强化学习框架与实践

目前常用的深度学习框架（如 PyTorch、TensorFlow）都可以用来构建深度强化学习模型：

• 可以使用 OpenAI Gym 或 Gymnasium 等环境来测试和调试算法，比如经典的 CartPole、MountainCar、Atari 游戏等。
• 有许多现成的 RL 代码库可供快速实验和对比，例如 Stable Baselines3 (SB3)、RLlib 等，它们实现了 DQN、PPO、A2C、SAC 等常见算法。

示例流程（以 DQN 在 Gym 环境中训练 CartPole 为例）：

1. import gym
2. 创建环境：env = gym.make('CartPole-v1')
3. 构建 DQN 神经网络，并初始化参数。
4. 训练循环：
   • 在环境中采样数据（状态、动作、奖励、下一状态）。
   • 存储到 replay buffer（经验回放），然后从其中随机采样一个小批量（batch）。
   • 计算 Q 目标值并更新网络参数。
5. 循环多轮后，评估 Agent 绩效：看能在多次测试中持续保持平衡。

7. 接下来如何学习

1. 选定一个简单的环境（如 OpenAI Gym 里的 CartPole）开始实践，先用最基础的 Q-Learning 理解一下离线更新过程。 理解**马尔可夫决策过程 (MDP)**中的理解价值函数、Bellman 方程、策略迭代、价值迭代等。
2. 再动手实现 DQN：需要将 Q 函数替换为神经网络，需要 Replay Buffer、Target Network 等技巧。
3. 实现基于表格方法（Tabular Methods，如 Q-Learning、Sarsa），以简单环境（离散状态空间）进行实践。
4. 尝试更高级的算法（如 PPO），理解策略梯度方法背后的原理，并对比它们在同一个环境中的效果差异。
5. 如果你有一定深度学习基础，可以使用 PyTorch 或 TensorFlow 直接编写，也可以利用 Stable Baselines3 这样的现成库来快速实验。
6. 实验过程中，多观察收敛曲线、积累训练曲线，理解怎样设计探索策略、奖励机制等。