下次机试将是基地建立以来最最最简单的一次
题目链接:https://ac.nowcoder.com/acm/contest/124021
密码:acm1123
签到题A、D
简单题F、G、K
中等题J、C、E
难题H、B、I、L
A.沙漏Ⅱ
该题为签到题
思路:如图所示1和2是完全相同的,只要画出1然后复制粘贴,最后封底封顶即可,封底和封顶也是重复的,如何打印代码注释中详细说明
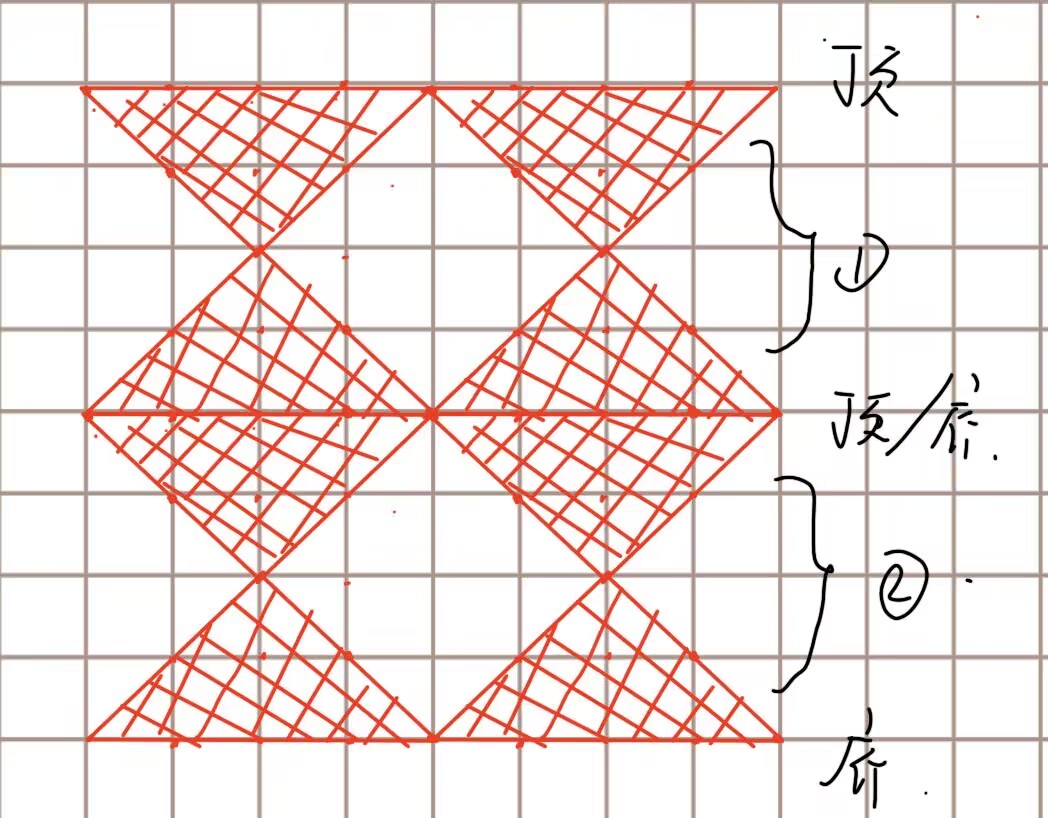
最上面的一行长度为((n * 2) - 1) * 2 - 1或者n * 4 - 3
#include<stdio.h>
// #define int long long
void solve()
{
int n;
scanf("%d",&n);
/////////最上面一行封顶
for(int i = 1; i <= ((n*2)-1)*2-1; i++){
printf("*");
}
printf("\n");
/////////////第一部分//////////////////////////////
//倒三角形(不打印尖和底)
for(int i = 1; i <= n-2; i++){
//最前面空格
for(int j = 1; j <= i; j++){
printf(" ");
}
//第一个三角形
for(int j = 1; j <= (2 * n - 1) - 2 * i; j++){
printf("*");
}
//中间空格
for(int j = 1; j <= 2 * i - 1; j++){
printf(" ");
}
//第二个三角形(和第一个三角形一样)
for(int j = 1; j <= (2 * n - 1) - 2 * i; j++){
printf("*");
}
//换行
printf("\n");
}
//三角形(打印尖和底)
for(int i = n - 1; i >= 1; i--){//反过来即可
//最前面空格
for(int j = 1; j <= i; j++){
printf(" ");
}
//第一个三角形
for(int j = 1; j <= (2 * n - 1) - 2 * i; j++){
printf("*");
}
//中间空格
for(int j = 1; j <= 2 * i - 1; j++){
printf(" ");
}
//第二个三角形(和第一个三角形一样)
for(int j = 1; j <= (2 * n - 1) - 2 * i; j++){
printf("*");
}
//换行
printf("\n");
}
///////////////////////////////////////////////////////////
///最上面一行封顶
for(int i = 1; i <= ((n*2)-1)*2-1; i++){
printf("*");
}
printf("\n");
///////////////第二部分(复制第一部分即可)////////////////
//倒三角形(不打印尖和底)
for(int i = 1; i <= n-2; i++){
//最前面空格
for(int j = 1; j <= i; j++){
printf(" ");
}
//第一个三角形
for(int j = 1; j <= (2 * n - 1) - 2 * i; j++){
printf("*");
}
//中间空格
for(int j = 1; j <= 2 * i - 1; j++){
printf(" ");
}
//第二个三角形(和第一个三角形一样)
for(int j = 1; j <= (2 * n - 1) - 2 * i; j++){
printf("*");
}
//换行
printf("\n");
}
//三角形(打印尖和底)
for(int i = n - 1; i >= 1; i--){//反过来即可
//最前面空格
for(int j = 1; j <= i; j++){
printf(" ");
}
//第一个三角形
for(int j = 1; j <= (2 * n - 1) - 2 * i; j++){
printf("*");
}
//中间空格
for(int j = 1; j <= 2 * i - 1; j++){
printf(" ");
}
//第二个三角形(和第一个三角形一样)
for(int j = 1; j <= (2 * n - 1) - 2 * i; j++){
printf("*");
}
//换行
printf("\n");
}
/////////////////////////////////////////
//封底最下面一行(和最上面一行一样)
for(int i = 1; i <= ((n*2)-1)*2-1; i++){
printf("*");
}
printf("\n");
}
signed main()
{
int t=1;
// scanf("%lld", &t);
while(t--)
{
solve();
}
return 0;
}
B.城市规划
这个题就是一个区间和并的模板题,但是对不会排序或者没学C++的来说确实有点难,就是输入区间之后对每个区间进行排序(先按l的大小升序,再按r的大小进行升序),然后遍历有区间重合就合并就好了。
#include<stdlib.h>
//#define int long long
int cmp(const void *a, const void *b) {//排序规则
const int *A = (const int*)(a);
const int *B = (const int*)(b);
if (A[0] != B[0]) {
return A[0] - B[0];
}
return A[1] - B[1];
}
void solve() {
int n;
// cin >> n;
scanf("%d",&n);
int q[100001][2] = {};
for (int i = 0; i < n; i++) {
// cin >> q[i][0] >> q[i][1]; //0存l,1存r
scanf("%d %d",&q[i][0],&q[i][1]);
}
qsort(q,n,sizeof(q[0]),cmp);//排序
int a[n][2], s = 0, st = -2e9, ed = -2e9;
for (int i = 0; i < n; i++) {//合并区间
if (q[i][0] > ed) {//判断区间是否重合
if (st != -2e9) {
a[s][0] = st;
a[s++][1] = ed;
}
st = q[i][0], ed = q[i][1];//更新下一个区间
} else
{
if(q[i][1]>ed)//重合更新区间的右边界
ed=q[i][1];
}
}
if (st != -2e9) {
a[s][0] = st;
a[s][1] = ed;
}
// cout << s << endl;
printf("%d\n",s+1);
for (int i = 0; i <= s; i++) {
// cout << a[i][0] << ' ' << a[i][1] << endl;
printf("%d %d\n",a[i][0],a[i][1]);
}
}
signed main() {
// ios::sync_with_stdio(0);
// cin.tie(0), cout.tie(0);
int t = 1;
//cin>>t;
while (t--) {
solve();
}
return 0;
}
这个是C++代码会简单很多,因为C++中sort默认升序排序(二维也是一样的),用二维数组排序的话是(sort(q,q+n))
#include<bits/stdc++.h>
#define int long long
using namespace std;
void solve()
{
int n;
cin>>n;
vector<pair<int,int>> q(n),s;
for(int i=0;i<n;i++)
{
cin>>q[i].first>>q[i].second;
}
sort(q.begin(),q.end());
int st=-2e9,ed=-2e9;
for(int i=0;i<n;i++)
{
if(q[i].first>ed)
{
if(st!=-2e9)
{
s.push_back({st,ed});
}
st=q[i].first,ed=q[i].second;
}
ed=max(ed,q[i].second);
}
if(st!=-2e9)
s.push_back({st,ed});
cout<<s.size()<<endl;
for(int i=0;i<s.size();i++)
{
cout<<s[i].first<<' '<<s[i].second<<endl;
}
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
int t=1;
//cin>>t;
while(t--)
{
solve();
}
return 0;
}
C.1234?1432
题目有多种写法,这里给出递归写法思路,给出了n=2^k,n是2的次幂,所以每次都可以将n缩小一半直到为1。
根据图片提示我们知道每次可以将大的矩形分成四个小的矩形,进而我们可以将小的矩形分成四个更小的矩形。直到矩形大小为2。
#include<stdio.h>
int m[1500][1500];
int t = 1;
void met(int x, int y, int a, int b){//(x,a)和(y,b)分别为现在矩形的最左上和最右下坐标
if(x+1==y){
//左上
m[x][a] = t++;
//右下
m[y][b] = t++;
//左下
m[y][a] = t++;
//右上
m[x][b] = t++;
return ;
}
//左上
met(x, x + (y - x - 1) / 2, a, a + (b - a - 1)/2);
//右下
met(x + (y - x - 1) / 2 + 1, y, a + (b - a - 1) / 2 + 1, b);
//左下
met(x + (y - x - 1) / 2 + 1, y, a, a + (b - a - 1)/2);
//右上
met(x, x + (y - x - 1) / 2, a + (b - a - 1) / 2 + 1, b);
}
void solve()
{
int k;
scanf("%d",&k);
if(k==0){
printf("1");
return ;
}
int n = (int)pow(2, k);
met(1,n,1,n);
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++){
printf("%d ",m[i][j]);
}
printf("\n");
}
}
int main(){
int t = 1;
// cin >> t;
while(t--)solve();
return 0;
}
D.银元
很简单的一道题,大家都推出结果了,但是不仔细读题,题目写了数字可能很大,可以用字符串读入
因为题目上说每次只翻转 N-1 个,等价于只翻转一个,所以 N 个需要 N 次
直接输入输出就好
#include <stdio.h>
int main() {
char str[2010];
scanf("%s", str);
printf("%s\n", str);
return 0;
}
E.租车
一道最短路题目,涉及到图论了
#include<stdio.h>
#include<string.h>
int a[210][210];
int min(int a,int b){
return (a<b?a:b);
}
void egde(int u,int v,int x){
a[u][v]=x;
}
int main()
{
int n;
scanf("%d",&n);
memset(a,0x3f,sizeof(a));
//从1开始建图,方便书写
for(int i=1;i<=n;i++)
for(int j=i;j<=n;j++){
if(i==j)a[i][j]=0;
else{
int x;
scanf("%d",&x);
egde(i,j,x);
}
}
//下面是floyd模板 是一种最短路算法
for(int k=1;k<=n;k++)//floyd
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
// 就是从 i 到 j 的过程中,能不能借助第三点 k 使得距离更小
a[i][j]=min(a[i][j],a[i][k]+a[k][j]);
}
printf("%d",a[1][n]);
return 0;
}
F.神秘的二进制Ⅱ
和上一次神秘的二进制相比将^(按位与)换成了|(逻辑或),逻辑或的运算是二进制位下,有1就为1,那么将所有数都进行逻辑或即可得到最大值
#include<stdio.h>
void solve()
{
int n;
scanf("%d", &n);
int a;
scanf("%d", &a);
int sum = a;
for(int i = 2; i <= n; i++){
scanf("%d", &a);
sum = sum | a;
}
printf("%d", sum);
}
int main(){
int t = 1;
// cin >> t;
while(t--)solve();
return 0;
}
G.神秘序列
该题需要开long long

通过序列 [1,1,2,4,8] 我们发现第二项开始,后一项等于前一项的两倍。
还是通过序列 [1,1,2,4,8] 我们发现除了第一,二个数,每个数都是偶数
题目要我们求包含x的序列最后一个数的最小可能值,我们可以考虑寻找x作为最后元素时的序列最长长度t,若该长度大于n,x即为我们所求,否则结果为x * pow(2,n-t)。
同时第一,二个数可以为奇数所以一开始就可以提供t=2的长度,我们寻找第一个奇数,一开始t为2。
int y = x;
int t = 2;
while(y/2==0){
y/2;
t++;
}
AC代码
#include<stdio.h>
void solve(){
long n, x;
scanf("%d %d",&n,&x);
long long t = 2, y = x;
while(y%2==0){
t++;
y/=2;
}
if(t>=n)
printf("%lld\n",x);
else
printf("%lld\n",x*(long long)pow(2, n - t));
}
int main()
{
long long t = 1;
scanf("%d",&t);
while(t--)
solve();
return 0;
}
其他解(1)
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=25;
int s[N]={};
void cheak()
{
s[1]=1,s[2]=1;
for(int i=3;i<25;i++)
{
s[i]=2*s[i-1];
}
}
void solve()
{
int n,x;
cin>>n>>x;
for(int i=n;i>=1;i--)
{
if(x%s[i]==0)
{
cout<<s[n]*x/s[i]<<endl;
return;
}
}
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
int t=1;
cin>>t;
cheak();
while(t--)
{
solve();
}
return 0;
}
其他解(2)
#include<bits/stdc++.h>
#define int long long
using namespace std;
void solve()
{
int n,x;
cin>>n>>x;
for(int i=n;i>=1;i--)
{
if(x%(int)pow(2,i-2)==0)
{
cout<<(int)pow(2,n-2)*x/(int)pow(2,i-2)<<endl;
return;
}
}
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
int t=1;
cin>>t;
while(t--)
{
solve();
}
return 0;
}
H.古籍修复
//这个可能比较难,用C语言存字符串的话会比较麻烦,可以用C++的string
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;
string get_(string str) {
//如果字符串为空就返回空
if (str.empty()) {
return "";
}
//截取字符串第一个,res是答案字符串的意思
string res = str.substr(0, 1);
//str.size() 是获取字符串长度的意思
for (int i = 0; i < str.size(); i++) {
int l = i, r = i;//定义左右边界
//开始往两边放大,这是奇数的,因为起始位置相同,如果要移动那么l和r就会一起动,所以结果一定为奇数
while (l >= 0 && r < str.size() && str[l] == str[r]) {
int h = r - l + 1;//计算长度
if (h > res.size()) {//比长度
res = str.substr(l, h);
}
else if (h == res.size()) {
string s = str.substr(l, h);//截取答案字符串
if (s < res) {//注意 string 可以直接用">","<","=="来比字典序的
res = s;
}
}
//两个同时移动
l--;
r++;
}
//现在是偶数,道理同上
l = i;
r = i + 1;
while (l >= 0 && r < str.size() && str[l] == str[r]) {
int h = r - l + 1;
if (h > res.size()) {
res = str.substr(l, h);
} else if (h == res.size()) {
string s = str.substr(l, h);
if (s < res) {
res = s;
}
}
l--;
r++;
}
}
return res;
}
int main() {
string str;//字符串
cin>>str;//读入 这里的cin相当于scanf
cout <<get_(str) << '\n'; //输出 这里的cout相当于printf
return 0;
}
I.数之王国
J.找规律??
根据数组可以发现,上面是奇数,下面是质数。
题目要求第n个数的小数形式,第n个奇数为2*n-1。
我们需要求第n个质数.
首先我们需要判断质数,这里给出试除法。
int isPrime(int x){
if(x==1)
return 0;
if(x==2)
return 1;
//遍历到 √x 而非 x-1
//是因为若 x 有大于 √x 的因数
//必然对应一个小于 √x 的因数
//能减少循环次数,提高效率。
for(int i = 2; i * i <= x; i++){
if(x%i==0){
return 0;
}
}
return 1;
}
然后我们求第n个质数
int n;
cin >> n;
int f = 0;
int sum = 2;
for(int i = 1;; i++) {
if(isPrime(i))
f++;
if(f==n){
sum = i;
break;
}
}
第n个质数即为sum.
但是题目有t个(1 ≤ t ≤ 1e6)测试用例。
如果刚好题目有1000000个测试用例,每一次我们都重新从第一个质数判断到第n个质数,而n又都是第100000个,一定会超时。
我们发现我们每次求第n个质数时,前n-1个质数其实也被我们找出来了,所以我们想到可以用数组将这n个质数都存下来。
int a[100000+10];
for(int i = 2;f<=1e5; i++) {
if(isPrime(i)){
a[f++]=i;
}
}
至此我们可以快速找出第n个数即为(n*2-1)/a[n];
AC代码
#include <stdio.h>
// int a[1299709+10];
int a[100000+10];
int f = 1;
int isPrime(int x){
if(x==1)
return 0;
if(x==2)
return 1;
//遍历到 √x 而非 x-1
//是因为若 x 有大于 √x 的因数
//必然对应一个小于 √x 的因数
//能减少循环次数,提高效率。
for(int i = 2; i * i <= x; i++){
if(x%i==0){
return 0;
}
}
return 1;
}
void solve()
{
int n;
scanf("%d",&n);
printf("%.6lf\n",(double)(n * 2.0 - 1) / (a[n]) * 1.0);
// printf("%d",a[100000]);//1299709
}
int main()
{
for(int i = 2;f<=1e5; i++) {
if(isPrime(i)){
a[f++]=i;
}
}
int t = 1;
scanf("%d",&t);
while(t--) solve();
return 0;
}
K.匹配
这道匹配,可能引起歧义了,就是给定一串字符串,字符串中有括号有其它字符
我们只需要判断括号是否匹配就好了
也就是说我们需要忽略除括号以外的字符
这道题用栈来写会简单一些,当然也可以用C语言的char字符串来写,如果要用char字符串来写的话,就类似于栈嘛
栈是一种先进后出的数据结构,大家可以把它想象成弹夹压子弹(先压进去的子弹不是后面才射出来吗)
#include <iostream>
#include <stack>
#include <string>
using namespace std;
//判断是不是左半边括号
bool z(char s) { return s == '(' || s == '{' || s == '['; }
//判断是不是右半边括号
bool y(char s) { return s == ')' || s == '}' || s == ']'; }
//判断能不能匹配
bool d(char l, char r) {
return (l == '(' && r == ')') || (l == '{' && r == '}') || (l == '[' && r == ']');
}
bool is(const string& s) {
stack<char> st;
for (int i=0;i<s.size();i++) {
char ch=s[i];
if (z(ch)) {//如果是左括号就入栈
st.push(ch);//这个是入栈的函数
} else if (y(ch)) {//如果是右括号
//empty()是检查栈是否为空的函数,如果为空,不就是只有右括号嘛
//top()是返回栈顶的
//pop()是弹出栈顶的元素
//判断是否匹配
if (st.empty()) return false;//先判空
char c = st.top();
st.pop();//再取顶并弹出
if (!d(c, ch)) return false;//不匹配直接失败
}
}
return st.empty();
}
int main() {
string str;
cin >> str;//读入一个字符串
//这里是判断是否匹配
if (is(str)) {
cout << "Yes" << endl;
} else {
cout << "No" << endl;
}
return 0;
}
L.折得玫瑰花一朵
其实就是dfs
#include <stdio.h>
#include <stdbool.h>
bool f[21][21];//记录是否有路径相连
int a[21];//记录玫瑰数
int path[21], ans[21], cnt; //path记录路径,ans记录答案,cnt记录走了多少个点
bool b[21];//记录该点是否走过
int n;
int maxx;//记录挖的最大玫瑰数
// 检查是否还能继续往下挖
bool chck(int x) {
for (int i = 1; i <= n; i++) {
if (f[x][i] && !b[i]) return false;
}
return true;
}
//x记录现在位置,stp记录走了几个点,sum记录挖的玫瑰数
void dfs(int x, int stp, int sum) {
if (chck(x)) {
if (maxx < sum) {//更新最大值和路径
maxx = sum;
cnt = stp;
for (int i = 1; i <= stp; i++)
ans[i] = path[i];
}
return;
}
//寻找下一个能去的地方
for (int i = 1; i <= n; i++) {
if (f[x][i] && !b[i]) {
b[i] = true;//标记走过
path[stp + 1] = i;//记录路径
dfs(i, stp + 1, sum + a[i]);
b[i] = false;//回溯
}
}
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++)
scanf("%d", &a[i]);
for (int i = 1; i < n; i++) {
for (int j = i + 1; j <= n; j++) {
int t;
scanf("%d", &t);
f[i][j] = (t != 0); //这里是单向边,仅读上三角f[i][j]
}
}
maxx = 0;
cnt = 0;
for (int i = 1; i <= n; i++) {
b[i] = true;
path[1] = i;//记录起点
dfs(i, 1, a[i]);
b[i] = false;
}
for (int i = 1; i <= cnt; i++)
printf("%d ", ans[i]);
printf("\n%d", maxx);
return 0;
}




















 344
344

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








