吴恩达nlp

最新推荐文章于 2025-07-07 11:13:17 发布

转载最新推荐文章于 2025-07-07 11:13:17 发布 · 175 阅读

CC 4.0 BY-SA版权

原文链接：https://ogmxx.blog.youkuaiyun.com/article/details/114989382?fromshare=blogdetail&sharetype=blogdetail&sharerId=114989382&sharerefer=PC&sharesource=ywdataanalyst&sharefrom=from_link

文章标签：

#深度学习 #人工智能

1.2 情感分析与朴素贝叶斯法(Sentiment Analysis with Naïve Bayes)

1.概率论基础

1.1 单事件概率

定义：一个事件发生的概率
例如：设事件A表示"一个文本是正向文本"，则其发生概率P(A) = 正向文本数 / 总文本数
下图中，绿色格表示正向文本、橙色格表示负向文本，则P(A) = 绿格数 / 总格数 = 13/20 = 0.65 即表示从该语料库中任取一个文本其是正向文本的概率为0.65

1.2 多事件概率

定义：多个事件发生的概率
例如：设事件"正向文本出现happy"，由两个子事件构成，即

A：一个文本是正向文本 B：该文本中出现happy 其组合概率P(A,B) = P(A∩B) = 3/20

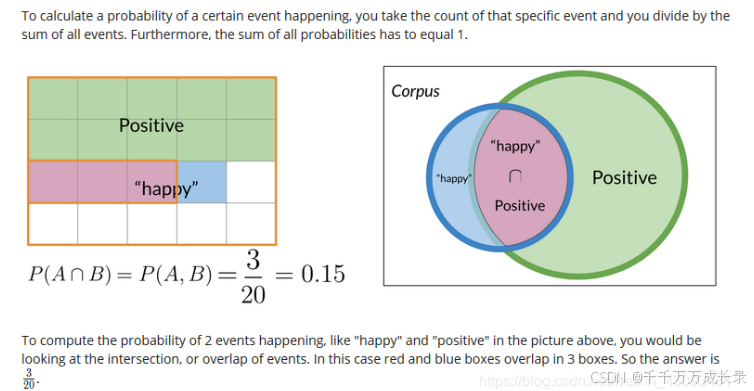
1.3 条件概率

定义：在已知事件B已经发生的情况下，事件A发生的概率，记作P(A|B)
计算法则：功能：能有效降低搜索空间
例：在已知一个单词是happy的情况下，该文本是正向文本的概率为P(Positive|"happy") = P(Positive ∩ "happy") / P("happy")
此时只需要在蓝色圈中进行搜索，极大减少了搜索范围

1.4 贝叶斯定理

定义：计算已知事件Y发生情况下，事件X的发生概率，由条件概率推广而来
公式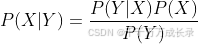：推导过程(略)

2.朴素贝叶斯法（Naïve Bayes）
2.1 基本概念

概述：朴素贝叶斯法是基于贝叶斯定理和条件独立假设的分类方法；属于概率分类器，是生成模型；实现简单，学习与预测效率高，常作为比较基准
简要流程：对于给定训练数据，首先基于条件独立假设学习输入输出的联合概率分布；然后基于模型，对给定的输入x，利用贝叶斯定理求出后验概率最大的输出y
条件独立假设：定义：用于分类的特征在类确定的条件下都是条件独立的，即

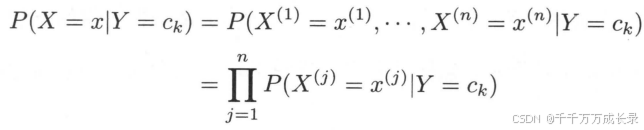
功能：该假设极大降低了计算复杂度、简化了模型，但同时牺牲了一定分类准确度

根据机器学习三要素，任何模型都由模型、学习准则(策略)、优化算法构成，含义如下：

模型：一个映射函数，输入数据输出预测结果，即该机器学习方法的功能和目的
学习准则：评价模型好坏的标准，预测值与真实值的差异的期望，可以认为是损失函数
优化算法：一个最优化问题，寻找最优模型的方法，即最小化损失函数的方法，机器学习的训练过程就是求解最优化问题的过程

2.2 朴素贝叶斯模型

定义：输入数据x，输出其最有可能出现在的类别y=ck的概率
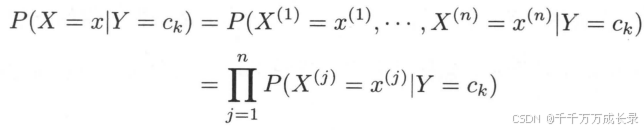
数学推导(略)

2.3 学习策略-极大似然估计(MLE)

概述：在朴素贝叶斯法中，学习意味着对先验概率和条件概率进行估计，因此可以使用极大似然估计法分别对这两部分进行估计
方法：

先验概率的极大似然估计：

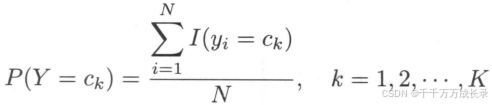
条件概率的极大似然估计：略

2.4 优化算法-后验概率最大化准则

定义：朴素贝叶斯法将结果分到后验概率最大的类中，就等价于期望风险最小化

2.5 优化技巧

2.5.1 拉普拉斯平滑 (Laplacian Smoothing)

原因：由于朴素贝叶斯法中通过累乘来计算最终概率，因此只要其中一个值为0，最终结果就会变为0，失去意义
功能：防止出现概率为0的情况，且仍保证概率和为1
方法：计算条件概率时，分子+1，分母+V(词汇表中不同单词的个数)；
例子：

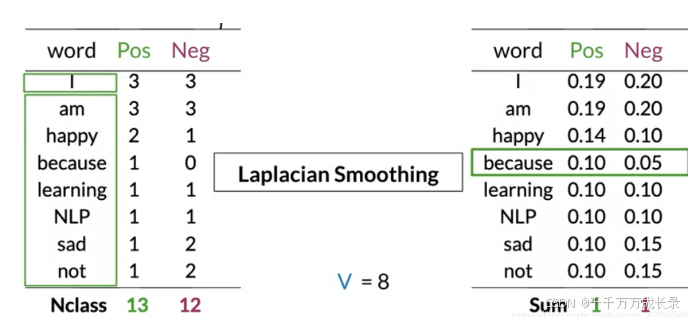
2.5.2 对数似然 (Log Likelihood)
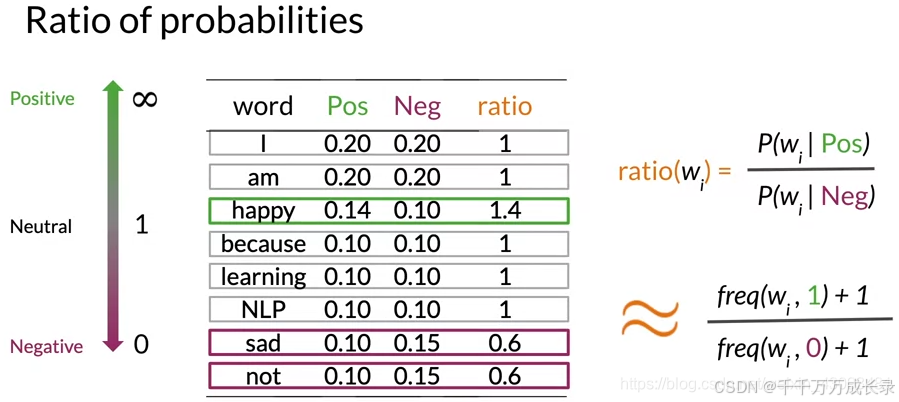
(1)概率比值(ratio)

定义：用正向条件概率/负向条件概率；越大于1越正向，越接近0越负向，等于1即中性

功能：判断一个词是正向还是负向

例：对于happy，ratio("happy") = 0.14 / 0.1 = 1.4 > 1，因此其为正向情感词

(2)对数先验(log prior)

定义：对数先验 = log(正向样本数 / 负向样本数)

功能：修正不平衡数据集的影响；对于已经平衡的数据集(正向文本数=负向文本数)，其对数先验为0，不产生影响

(3)对数似然(log likelihood)

定义：对概率比值再求log

原因：计算时连乘了很多小数，可能发生数值下溢

功能：可以避免数值过小发生下溢

例：

(4)对数先验+对数似然

功能：判断整个文本的情感倾向

定义：计算对数先验+对数似然的和；其值越大于0就越正向，越小于0就越负向，等于0为中性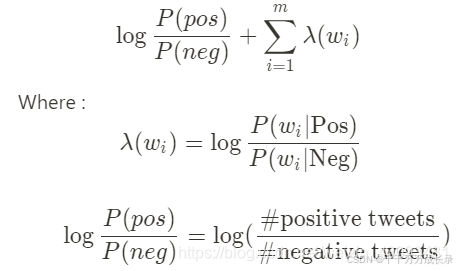

例子：

3.利用朴素贝叶斯法进行情感分析

3.1 整体流程

总体流程：

(1)获取数据

(2)数据预处理

(3)构建正负词频表：统计语料库中各个单词分别在正负文本中出现次数

(4)计算条件概率表：统计各单词在正向/负向文本中出现次数，分别除正向/负向文本总数，得到各单词在正向文本/负向文本中出现的概率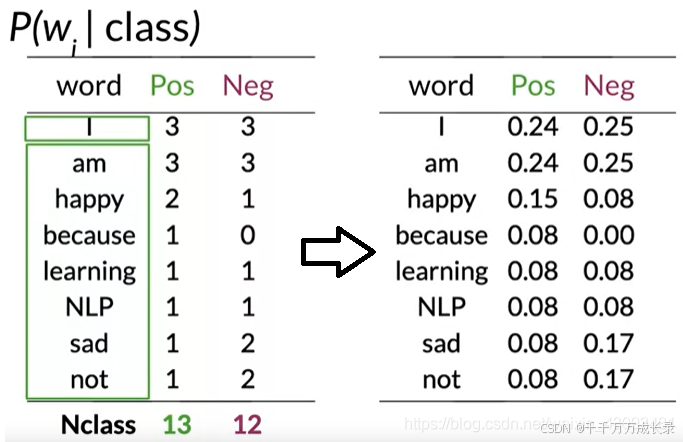

(5)计算各单词的对数似然λ：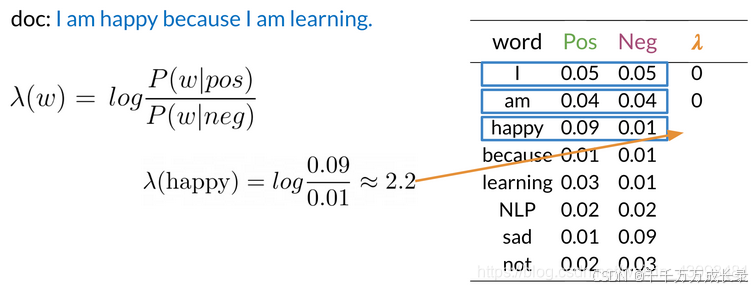

(6)计算对数先验：修正不平衡数据集的影响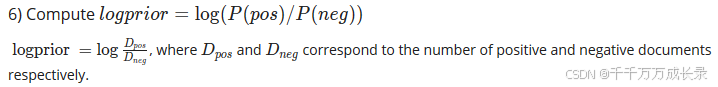

(7)进行预测：若对数先验+对数似然 >0 则为正向情感，反之为负向情感

3.2 模型评价

准确度：即预测正确文本数 / 总本文数

Xval Yval——>新文本上准确率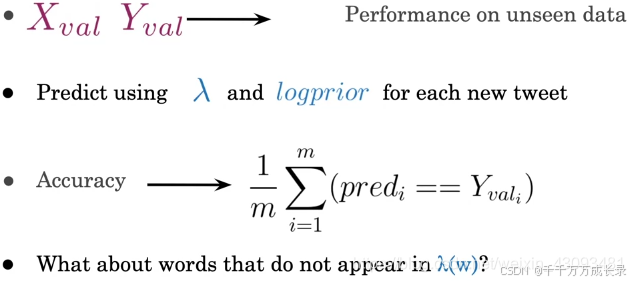

3.3 朴素贝叶斯法的其它应用

身份鉴别词义消歧过滤垃圾邮件等等

3.4 问题 / 缺点

(1)条件独立假设

原因：由于朴素贝叶斯法中使用了条件独立假设，假设句子中各单词间都是独立的，但显然一个句子的上下文间存在联系，因此会造成一定的错误

例子：如有些句话，若不考虑上下文，将无法准确预测出空缺处单词

(2)非平衡数据集

原因：在实际情况下，数据集往往是非平衡的，且存在许多噪音，该模型无法解决这些问题

(3)其他问题

去标点：某些情况下，标点会表达情感，甚至改变整句话含义

去停用词：中性词/非情感词在某些语境下也会表达情感如not!

语句顺序：不同的语序可能表达完全不同的含义

反讽/夸张：对人类很容易理解，但机器无法理解其深层含义

1.3 向量空间模型(Vector Space Models)

1.向量空间模型(Vector Space Models)

1.1 基本概念

定义：向量空间模型将单词或文本用向量表示，通过上下文来获取其语义信息

功能：识别两文本/两类文档间的相似度和独立性

例：单词基本相同的两句话可能有不同含义；而单词完全不同的两句话可能有相同含义

1.2 应用

信息提取机器翻译聊天机器人

2.构建向量空间

2.1 单词统计(Word by Word)

定义：统计指定窗口大小下，两词共同出现的次数

例子：当窗口大小k=2时，对于"data"为中心词，与其共同出现的词为："like","simple","simple","raw"

由此构建出向量data=[2,1,1,0]

2.2 文本统计(Word by Doc)

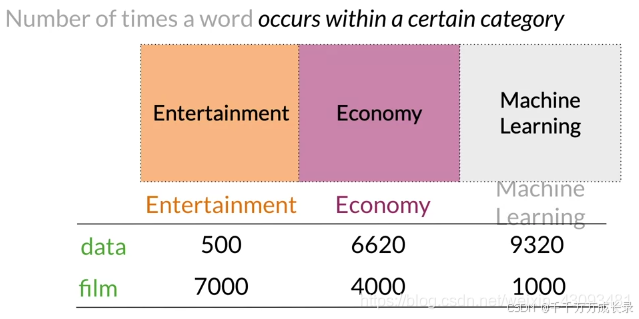
定义：统计单词在不同类别文档中出现的次数

例子：如下图，data在娱乐领域文本中共出现500次、在经济领域文本中共出现6620次，在机器学习领域文本中共出现9320次由此构建向量data=[500,6620,9320]

2.3 应用--衡量相似度

定义：通过在向量空间中进行一系列计算，可判断两向量间的相似度等

例：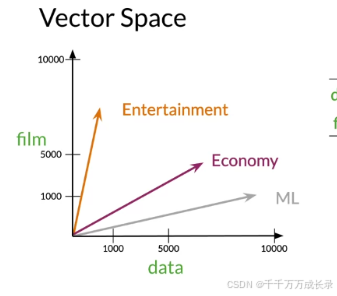

3.相似度衡量方法

3.1 欧氏距离(Euclidean Distance)

定义：衡量空间中两点间距离

缺点：当语料库大小不同时，使用欧氏距离比较会产生误差

计算方法：

(1)二维情况：

公式：

(2)n维情况：

公式：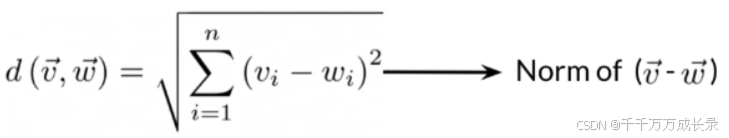

例：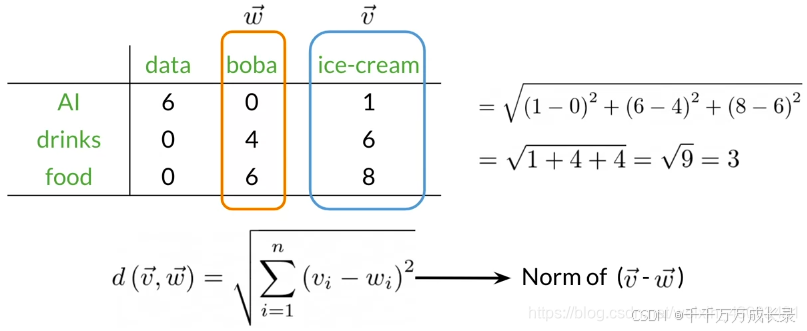

python实现：

3.2 余弦相似度(Cosine Similarity)

定义：衡量两向量间的夹角，即相似程度

优点：在比较不同大小语料间相似度时，余弦相似度更加准确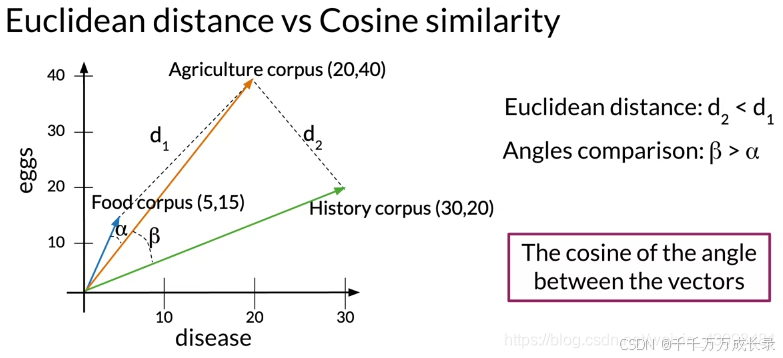

计算方法：

公式：

评估：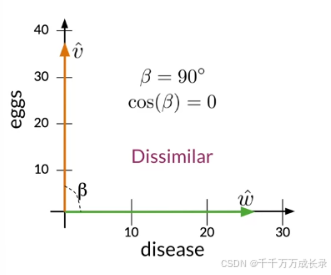

余弦相似度越小(接近0)，表示相似度越低；越大(接近1)，表示相似度越高

3.3 应用--首都预测

已知USA的首都是Washington，想得到Russia的首都，则可通过以下计算：

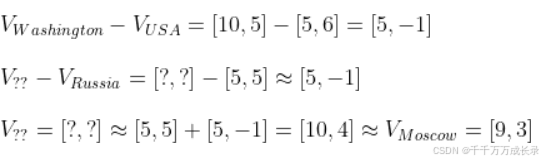
4.主成分分析 (PCA)

4.1 基本概念

定义：在尽可能不损失信息的情况，将高维向量投影至低维空间

功能：降维，从而使信息便于理解

4.2 PCA原理

概述：计算出各不相关特征的方向，然后在该方向上进行投影

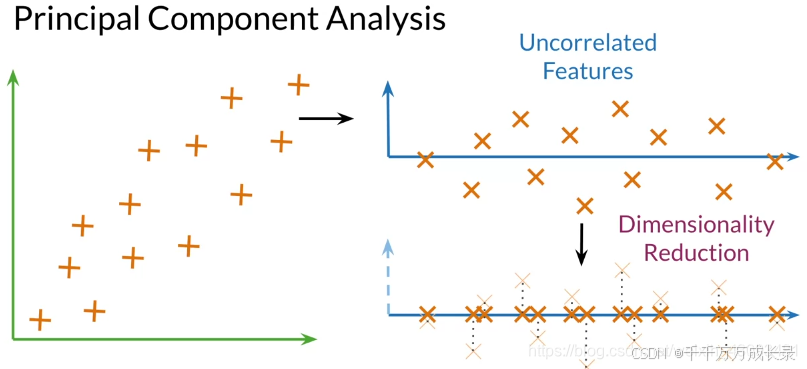
特征值与特征向量：

特征向量：数据中的不相关特征；包含了不相关特征的方向

特征值：每个特征中包含的信息；包含了新特征值的方差

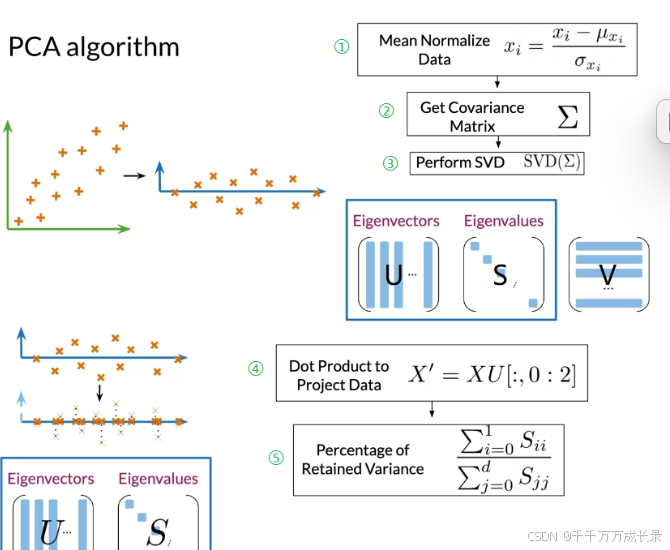
PCA算法流程：

(1)均值归一化数据：对每一个数据进行均值归一化

(2)计算协方差矩阵

(3)进行奇异值分析SVD，得到U、S、V三个矩阵

(4)通过点乘运算X'=XU，将不相关的特征数据投影至k维度

(5)计算保留方差的百分比

4.3 应用--数据可视化

定义：通过PCA将高维向量投影至三维以下，然后绘制出图形

功能：直观判断词向量效果，是否准确体现相关性

原文链接：https://blog.youkuaiyun.com/weixin_43093481/article/details/115051607

1.4 机器翻译与文件搜索(Machine Translation and Document Sear

1.词向量转换(Transforming word vectors)

1.1 基本原理

概述：先得到源语言和目标语言的词向量，再通过变换矩阵R将源语言的词向量转换成目标语言的词向量，距离转换后词向量最近的词向量即为最可能的翻译结果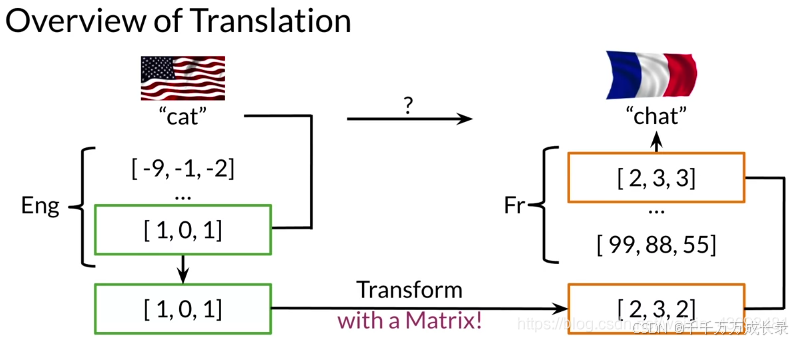

1.2 整体流程--利用梯度下降法计算转换矩阵R：

(1)通过弗罗贝尼乌斯范数计算损失值

(2)计算损失值的梯度

(3)用梯度更新R

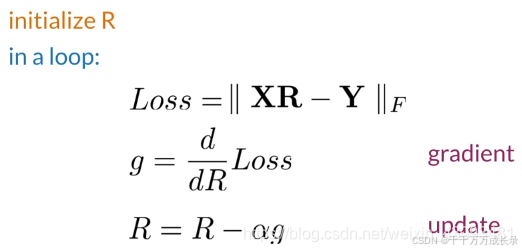
1.2.1 弗罗贝尼乌斯范数(Frobenus norm)

(1)弗罗贝尼乌斯范数

定义：衡量矩阵的大小；是针对于矩阵的范数，类比于对向量的L2范数

计算公式：即矩阵内各元素平方和再开根号

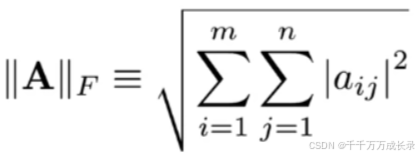
例：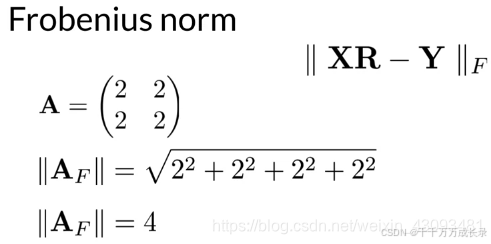

(2)平方弗罗贝尼乌斯范数(Frobenus norm squared)

定义：即弗罗贝尼乌斯范数的平方

python实现

1.2.2 计算梯度
使用平方弗罗贝尼乌斯范数作为损失函数，其导数计算如下：

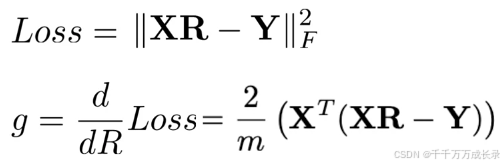
2.K-近邻算法(K-nearest neighbors)

2.1 基本概念

功能：在翻译时，使用变换矩阵R对源词向量X进行变换，但变换后的词向量XR并不能完全对应目标语言的词向量，因此需要算法搜索最相近的词向量选为最终结果

例："hello"经过R矩阵变换后，得到目标词向量XR，需要选择距离目标词向量最近的词向量作为结果，即从"salut"和"bonjour"中选择距离最近的

常用方法：

局部敏感哈希：基于哈希表的方法，通过一种精巧的哈希函数，使得相邻元素能被最大概率分到同一桶中，在同一桶中进行搜索，以减少搜索空间
KD树：基于分层划分与二叉树的方法，通过使用一种特殊的数据结构，来减少搜索空间，从而加快搜索速度

2.2 近似最近邻搜索(Approximate nearest neighbors，ANN)

定义：一类通过牺牲一定准确度来换取更快的搜索速度的方法，能够在较短时间内找出任何查询点的最近点

原因：搜索整个空间十分缓慢，而通过ANN方法，能够在确保一定准确度的情况下，极大加快搜索速度

功能：更高效计算K近邻问题

原理：将空间用多组随机平面划分，如果两个点相距很近，则其有很大概率被划分在同一子空间，因此不用搜索全部空间，而是在每个子空间内进行搜索

实现：

2.3 局部敏感哈希(Locality sensitive hashing)

定义：一种ANN方法，通过一种精妙的哈希函数，将高维空间中的相近点映射到同一桶中，而后在相同桶中进行搜索已减少搜索空间

2.3.1 哈希函数与哈希表
定义：将向量映射为一个哈希值，加快计算速度

原理：高维空间中相邻的数据经过哈希函数映射到低维空间后，落入同一桶的概率很大，而不相邻的数据映射到同一桶的概率很小

实现：

2.3.2 具体方法
(1)超平面划分

定义：通过划分超平面，将原数据空间分割为多个子空间 plane

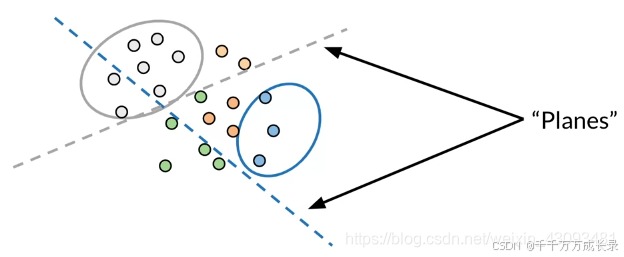
方法：对于每个向量v，在超平面上与法线向量进行点乘运算，点乘结果的符号，说明其所在方向

例：点乘结果为正，表明两向量同向；结果为负，表明两向量反向

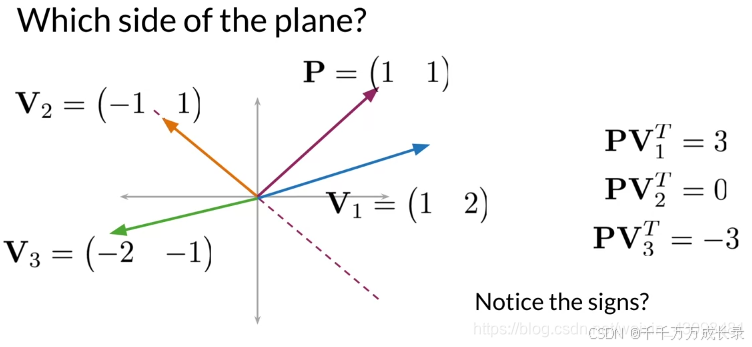
实现：

(2)哈希值计算

公式：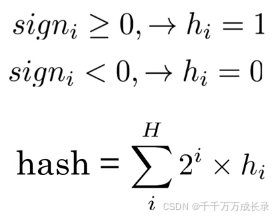

例：通过点乘结果的符号来计算哈希值，为正h=1，为负h=0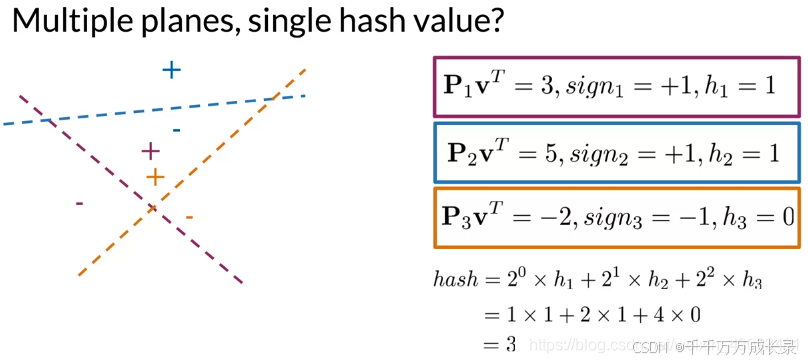

实现：

3.应用

3.1 机器翻译

概述：通过词向量变换与k近邻搜索，将源语言词向量转换为目标语言词向量，再使用k近邻算法找出最接近的一项，即为翻译结果

3.2 文档搜索

文档表示：一个文档可由其包含单词的词向量的和来表示；通过搜索与源文档词向量最近的目标文档词向量，即可找到与其含义最相似的文档

实现：

原文链接：https://blog.youkuaiyun.com/weixin_43093481/article/details/115101382

2.1 最小编辑距离算法与自动拼写纠正(Autocorrect)

1.自动纠正

1.1 基本概念

定义：自动将错误拼写修正为正确形式

整体流程：

(1)识别错误拼写单词

(2)计算最小编辑距离并构建候选编辑列表

(3)筛选候选编辑列表

(4)计算单词概率，选择最高概率词为结果

1.2 具体流程

构建模型：

(1)识别错误拼写词：

定义：如果一个词未存在于词汇表中即视为错误

(2)构建候选编辑列表：

编辑距离：将一个字符串变为另一个字符串所需要进行编辑操作的次数

编辑操作：

插入：增加一个字母
删除：删除一个字母
交换：交换两个相邻字母
替换：将一个字母换为另一个字母

例：

构建候选编辑列表：

定义：通过对4种编辑操作的组合，得到全部可能的情况构成编辑列表

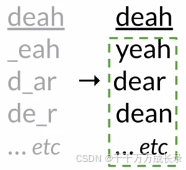
(3)筛选候选编辑列表：

定义：对编辑列表通过枚举进行填空后，只保留存在于词汇表中的单词(即拼写正确的单词)

(4)计算词概率：

词概率：该单词出现次数 / 总单词数

功能：评价一个词可能出现的概率，选择词概率最高的词作为纠正结果

2.最小编辑距离(Minimum edit distance)

2.1 基本概念

定义：将一个单词变为另一个单词所需的最少编辑操作数

功能：评估两个单词之间的相似度，两单词间编辑距离越小越相似

编辑操作：插入、删除、替换（注：在具体算法中，不考虑交换操作)

例：将"play" -> "stay"，需要两次替换操作，而一次替换操作的花费为2，因此总花费为2+2=4

应用：拼写校正文本相似度机器翻译 DNA测序...

2.2 最小编辑距离算法——一种经典动态规划(dp)算法

初始化：

源单词位于矩阵的列，目标单词位于矩阵的行
每个单词前的空字符#设为0

状态表示：

D[i,j]表示从源单词[0:i]到目标单词[0:j]所需的最小编辑距离
D[m,n]表示最终结果，即将源单词变为目标单词的最小编辑距离

状态转移方程：

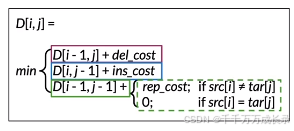
例子：对于D[1,1]位置，即p->s，可由三种方法实现：（更新为最小花费，因此D[1,1]=2）

插入+删除：p->ps->s，花费1+1=2
删除+插入：p->#->s，花费1+1=2
替换： p->s，花费2

最终结果：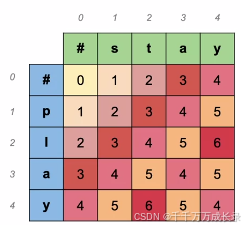
原文链接：https://blog.youkuaiyun.com/weixin_43093481/article/details/115188026

2.2 词性标注与隐式马尔科夫模型(Part of Speech Tagging and Hidden Markov Models)

1.词性标注(Part of Speech Tagging，POS)

1.1 基本概念

定义：标注出句子中各单词的词性，如名词、动词、形容词等

1.2 相关应用

命名实体识别指代消歧语音识别

2.马尔可夫链(Markov Chains)

2.1 基本概念

定义：离散时间的马尔可夫过程即马尔可夫链；其假设未来状态只与当前状态有关，而与时间无关

表示：可由有向图进行表示，同时可用邻近矩阵这种数据结构进行存储

例：若当前单词为动词，则下一个词有0.2的概率是动词、0.6的概率是名词

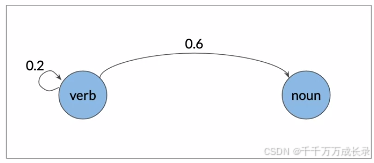
状态表示：

Q={q1,q2,q3}，表示各状态，即事件
箭头及权重表示各状态间的转移概率，即在当前状态下，下一个事件发生的条件概率

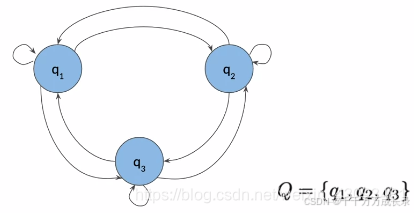
状态转移矩阵：

定义：对上述图形结构化表述，相当于邻接矩阵；横纵坐标表示各状态，值表示状态间的转移概率

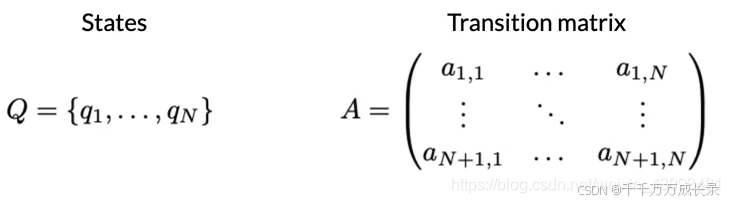
2.2 马尔可夫链与词性标注

状态表示：

定义：在词性标注任务中，各状态表示当前词的词性，而箭头则表示下一个词是某种词性的概率

例：当前词为"learn"，对应词性VB，而下一个词"something"，对应词性为NN；已知当前词为"learn"(VB)的情况下，下一个词为NN的概率为0.4

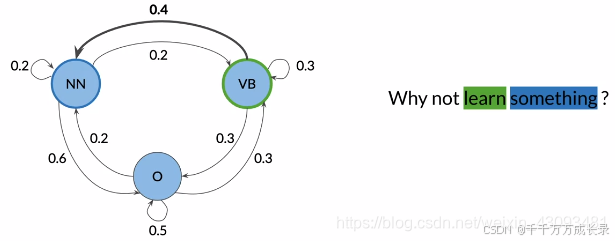
转移矩阵：

定义：在词性标注任务中，转移矩阵即各词性间转移的概率，是存储马尔可夫链的数据结构

例：

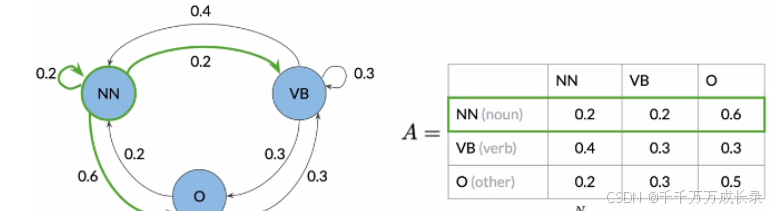
3.隐式马尔可夫模型(Hidden Markov Models)

3.1 基本概念

定义：模型中有状态是隐藏的即无法直接观察到

表示：用虚线圈表示隐藏状态，其他同马尔可夫链

例：在词性标注任务中，各单词的词性就是隐藏的，因为无法直接观察到如love 可以是名词可以是动词

3.2 状态转移概率

定义：由当前状态转移到另一状态的概率

例：已知蓝块+紫块的组合有2个，蓝块+任意颜色块的组合有3个因此已知当前为蓝块，下一个出现的是紫块的概率为2/3，即从蓝块转移到紫块的状态转移概率

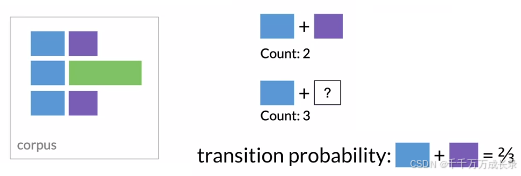
计算方法：

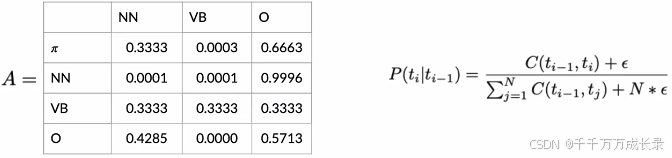
(1)计算各状态对出现次数C(ti-1，ti) (2)由ti-1状态转移到状态ti的概率，即：

计算状态转移矩阵：

(1)统计各状态对出现次数：

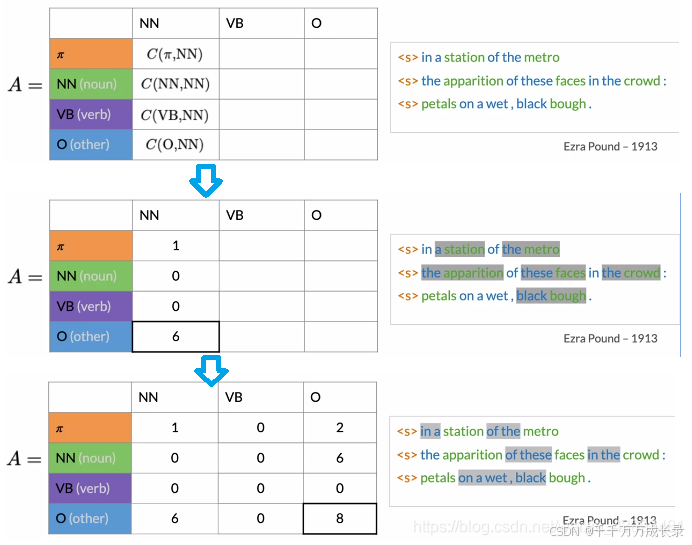
(2)平滑处理：避免出现除0错误

(3)计算各状态转移概率，构成矩阵：

3.3 发射概率(emission probabilities)

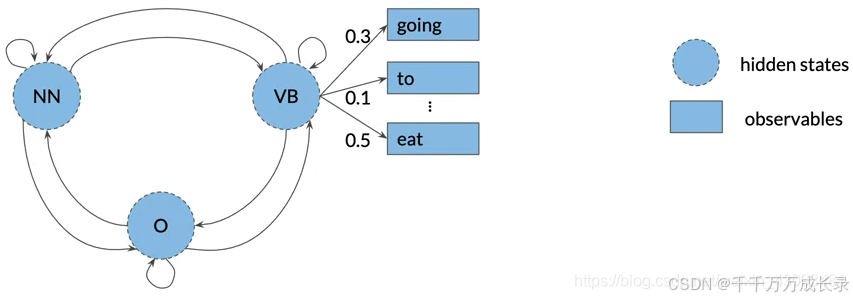
定义：从隐藏状态到可观察状态的状态转移概率

例：在词性标注任务中，则表示该词性对应到具体单词的概率如下图，若当前状态为动词VB，则有0.3的概率对应单词"going"、有0.1的概率对应单词"to"...

计算方法：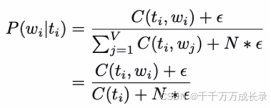

例：已知蓝块有3个，其中有2个对应单词"You"，一个对应单词"The" 因此，已知当前是蓝块，其对应单词为"You"的概率为2/3，即由蓝块到"You"的发射概率

计算发射矩阵：

(1)统计各状态对出现次数：

注：此处状态对为(词性，单词)状态对，与概率转移矩阵中不同

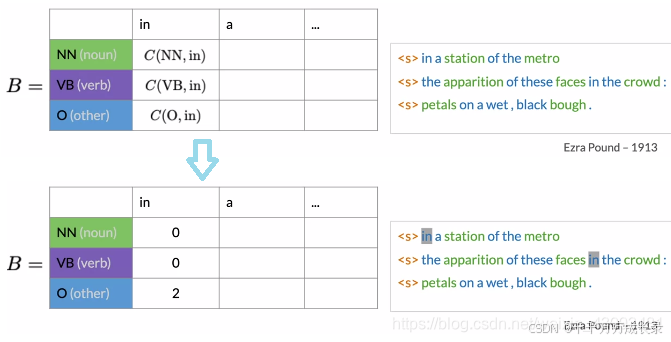
(2)平滑处理：略，同状态转移矩阵

(3)计算各发射概率，构成矩阵：

3.4 总结

状态表示：对应词性

状态转移矩阵A：一个词性转移到另一词性的概率

发射矩阵B：一个词性对应某个特定单词的概率

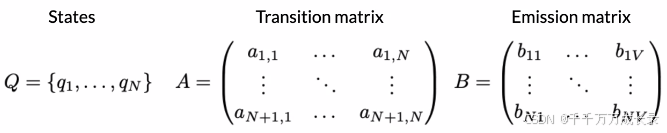
4.维特比算法(The Viterbi Algorithm)

4.1 基本概念

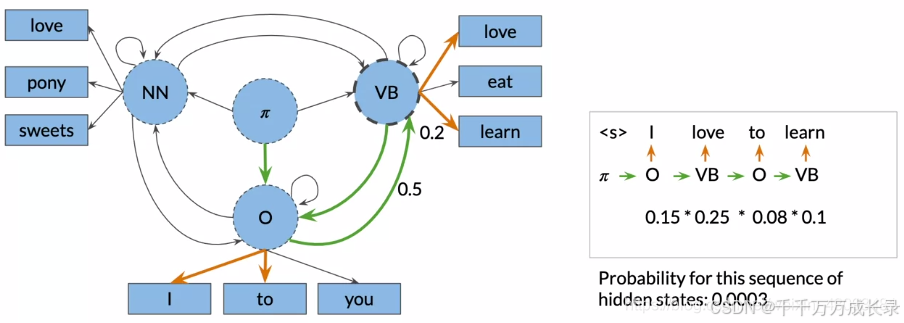
定义：一种图算法，能够找到概率最高的隐藏单元序列，即各单词最准确的词性标注

例：给定句子"I love to learn"，通过该算法能找出其概率最高的隐藏序列为"O->VB->O->VB"，即各单词对应的词性标注

方法：

三大步骤：初始化、前向传递、反向传递
两个辅助矩阵：

C矩阵：保存最优中间结果，即由前一状态经过一步转移到状态，并对应单词的最大概率
D矩阵：保存了路径，用于回溯找出最优结果

4.2 算法流程

4.2.1 初始化

C矩阵：

方法：将第一列初始化为，由初始状态经一步转移后，能得到句子中第一个词的概率；即句子中第一个词对应各词性的发射概率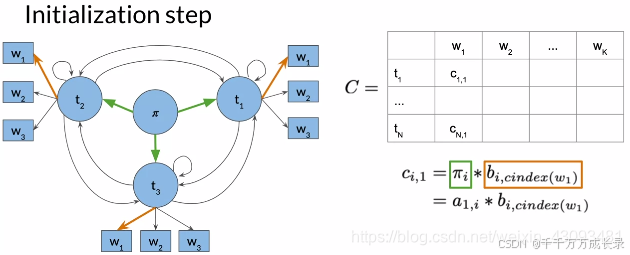

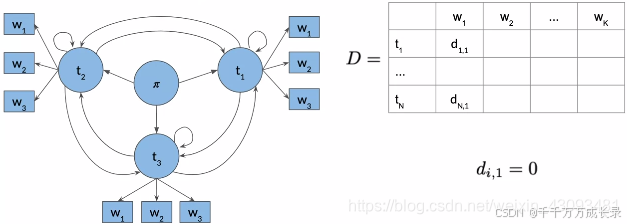
D矩阵：

方法：将第一列初始化为0，表示起始状态

4.2.2 正向传递

C矩阵：

方法：计算由任前一状态出发，经过一步转移后到达当前状态，且能得到当前单词的最大概率；计算所有可能情况，保存最大概率

计算公式：

优化：因连乘许多小数，可能导致数值下溢，因此可使用对数概率代替

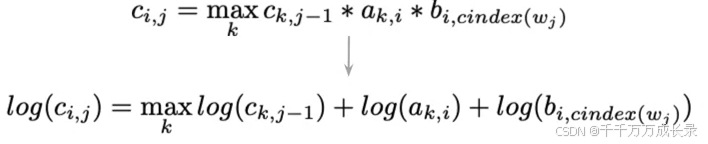
例：C(1,2)即由任前一状态出发，经过一步转移到达当前状态t1，且能得到句子中第2个单词的最大概率

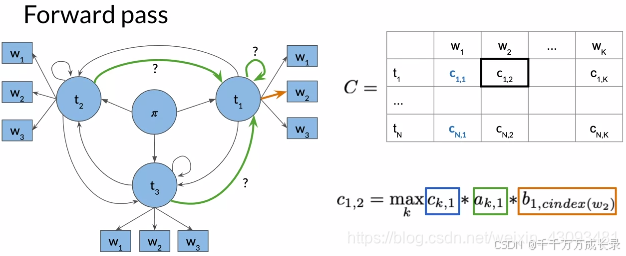
D矩阵：

方法：存储前一状态的索引；即由哪一状态转移到当前状态，能有最大概率得到当前单词

计算公式：

例：

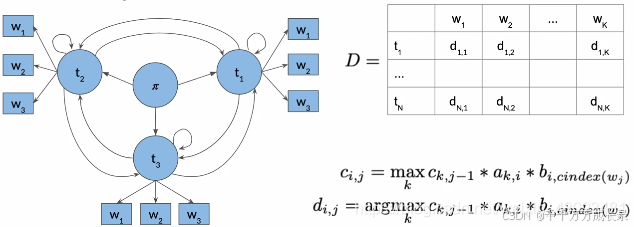
4.2.3 反向传递

功能：提取出概率最高的隐藏序列

步骤：

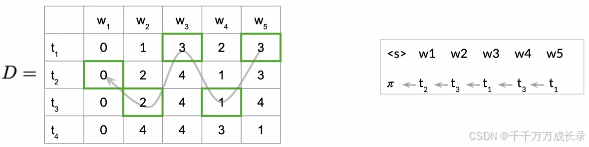
(1)计算C矩阵中最后一列中概率最高(最大值)项对应的索引s；

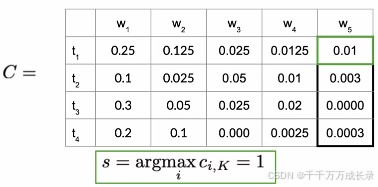
(2)通过该索引s在D矩阵中回溯，直到回到起始状态，通过路径还原得到最优序列

原文链接：https://blog.youkuaiyun.com/weixin_43093481/article/details/115253958

2.3 自动补全与语言模型(Autocomplete and Language Models)

1.N-Grams语言模型概述

1.1 基本概念

定义：一个N-gram就是一个由句子中连续单词构成的序列，其中N表示该序列中单词个数

三种常见n-gram：

Unigrams：一个单词构成一个序列
Bigrams：两个连续单词构成一个序列
Trigrams：三个连续单词构成一个序列

例：

功能：

(1)计算句子概率 (2)根据上文来估计下一个单词的概率

应用：语言识别、拼写纠正、辅助沟通系统...

句子自动补全：

(1)对文本进行预处理，使其适用于N-gram模型

(2)处理字典外单词

(3)平滑处理

(4)语言模型评估

1.2 N-grams与概率

序列表示：

定义：用Wi表示句子中的第i个单词，以此来代指整个句子

表示方法：上标 i 表示序列长度；下标 j 表示起始位置

例：即表示从句子中第一个单词开始，取之后连续m个单词

概率计算：

(1)Unigram概率计算：

方法：单词出现次数 / 句子长度，即单个单词的出现概率 (2)Bigram概率：

方法：两个单词一起出现的次数除前一个单词出现的次数

(3)Trigram概率：

方法：三个单词一起出现的次数除前两个单词一起出现的次数

例：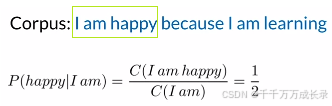

(4)N-gram probability：

方法：n个单词一起出现的次数除前n-1个单词一起出现的次数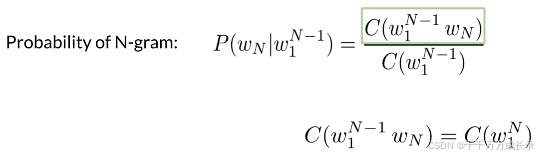

1.3 序列概率(Sequence Probabilities)

序列概率：

功能：计算整个句子(序列)的概率

方法：根据链式法则，依次计算条件概率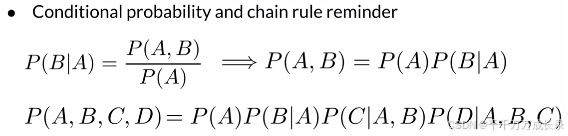

例：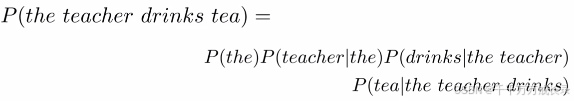

问题：句子较长部分可能不在语料库中，因此其出现次数为0，导致整个句子概率为0

马尔可夫假设：

定义：对于一个句子概率，只有最后N个单词重要，因此可以只考虑最后N个单词来近似计算整个句子的概率

功能：近似计算整个句子的概率，从而解决上述问题

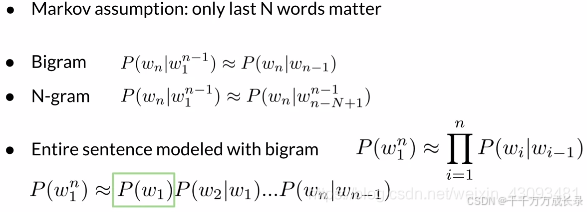
例：

1.4 起始符与终止符

起始符：

功能：统一计算方法，使得无需对第一个单词进行单独计算

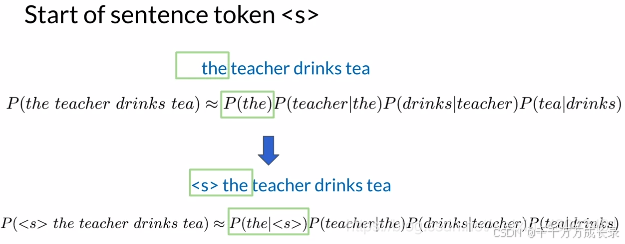
方法：N-gram模型中，前加N-1个起始符

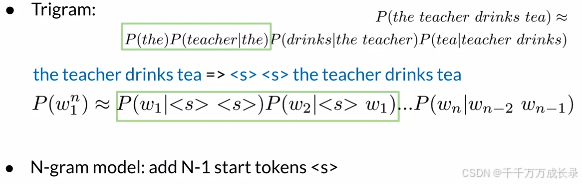
终止符：

方法：不管N为多少，只在句尾加一个终止符

例子：包含起始符与终止符情况下计算句子概率

2.N-Gram语言模型的构建与评估

2.1 整体流程

整体流程：

构建计数矩阵
构建概率矩阵
构建语言模型
引入对数概率
应用语言模型生成句子

2.2 具体流程

(1)构建计数矩阵：

方法：统计各n-gram出现次数

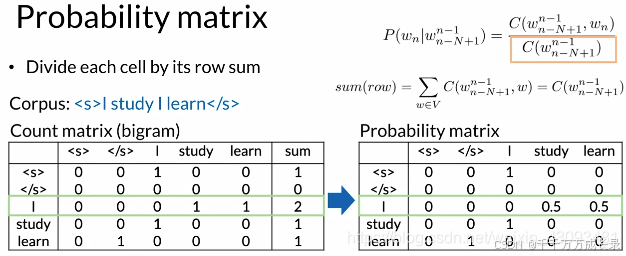
(2)构建概率矩阵：

方法：将计数矩阵中各元素除以各行总数和得到概率矩阵

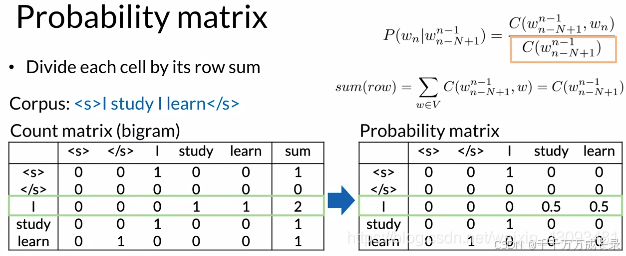
(3)概率矩阵与语言模型：

方法：通过概率矩阵，即可计算句子概率和下一个单词的概率

(4)对数概率：

原因：计算中很多<1的数连乘，可能造成数值下溢，因此使用对数概率避免该问题

(5)应用语言模型生成句子：

方法：选择起始符，通过概率矩阵选择下一个概率最高词，直到选择终止符，句子生成结束

2.3 模型评估

测试集：

定义：将语料库划分为训练集与测试集

拆分方法： (1)连续划分 (2)随机划分

困惑度(Perplexity)：

定义：一种评价句子语义清晰度的指标，困惑度越小句子语义越清晰，模型越好

计算方法：

例：bigram的困惑度计算

性质：困惑度越小，模型越好；字符模型PP<以单词为基础的模型PP

例子：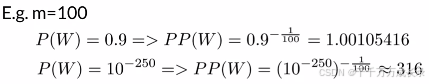

对数困惑度(Log perplexity)：

定义：对困惑度取对数

计数方法：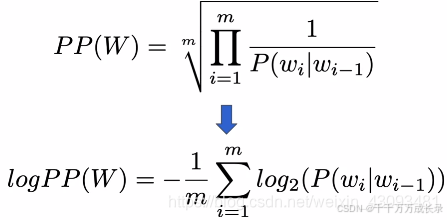

例子：可以看出N越大句子的困惑度越小，其语义越清晰

3.特殊情况处理

3.1 对词汇表外单词的处理

未知词：

定义：不存在于字典中的词

解决：使用<UNK>标识符代替

未知词处理：

步骤：

(1)创建词汇表

(2)对于未知词(即不在词汇表中的词)，使用<UNK>标识符代替

(3)计算<UNK>和其他词的概率

例子：

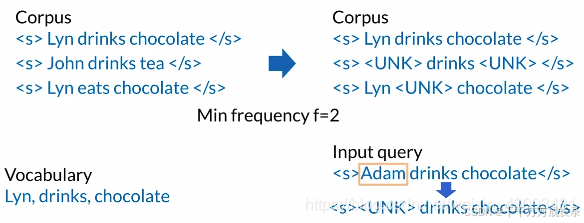
构建词汇表：

规定最小词频：即一个单词最少要在语料库中出现多少次才能被加入词汇表

3.2 对不存在序列的处理

原因：

不存在的N-grams会导致出现0，又由于进行连乘操作会使最终句子概率变为0

平滑法(Smoothing)：

方法：通过分子分母同加一个数来进行平滑，消除出现0的可能

回退法(Backoff)：

方法：当n-gram找不到时，进行回退，找(n-1)-gram

插值法(Interpolation)：

方法：给不同的n-gram设置不同的权重，且各之和为1，n越大权重越大，用加法代替连乘

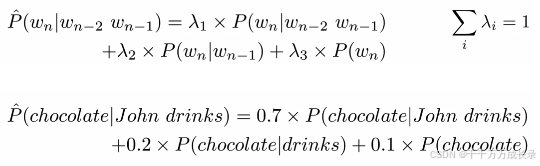
原文链接：https://blog.youkuaiyun.com/weixin_43093481/article/details/115337762

2.4 用CBOW实现词嵌入(Word embeddings with neural networks)

1.词的表示方法

1.1 整数表示

定义：每个词用一个整数表示

优点：简单

缺点：缺少语义信息

1.2 独热码表示(one-hot vectors)

定义：指定位置为1，其余位置为0

优点：简单、不用考虑单词间顺序

缺点：占用大量空间、无语义信息

1.3 词嵌入表示(Word Embedding)

定义：用一个向量表示一个单词，向量中每一维度都表示一种特定语义的强弱

优点：低维度(空间占用少)、包含丰富语义信息

原理：如下图所示，具有相近词义的词在向量空间中距离相近，因此词嵌入包含了语义信息

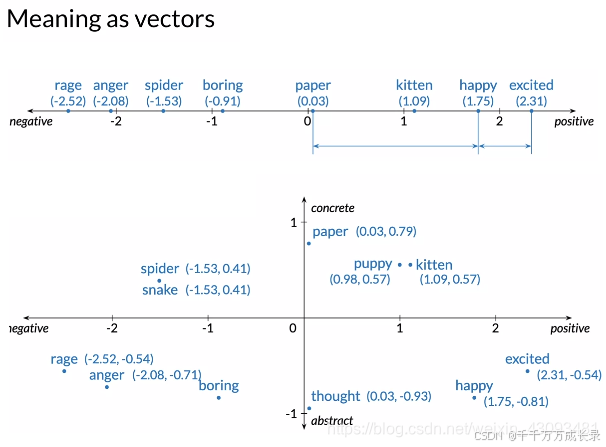
相关术语： 词向量：包含独热码表示和词嵌入表示两种表示方法

2.词嵌入的构建

2.1 整体流程

流程：先由语料库构建训练数据，再通过词嵌入方法训练模型，进而得到词嵌入

2.2 常见词嵌入方法

早期方法：word2vec ;Global Vectors fastText

3.数据处理

3.1 训练数据构建

训练集组成：上下文单词、中心词

构建方法：先指定窗口大小，然后滑动窗口遍历整个语料库，构建出训练数据集

3.2 数据预处理

3.2.1 数据清洗

方法：

小写化：构建词嵌入时不区分大小写，因为其语义相同
标点处理：常用标点统一用一个特殊符号表示；不常用标点直接删除
数字：根据任务不同，决定是否保留
特殊字符：通常直接删除
特殊文字：如表情、标签等，根据任务决定是否保留

Python实现：

常用库： nltk(.tokenize)

数据清洗实现：

滑动窗口实现：

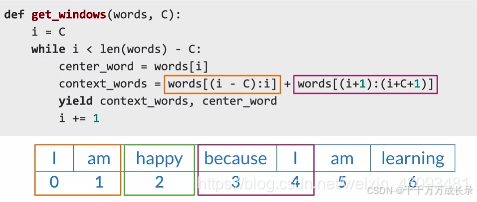
3.2.2 词向量化

中心词处理：将中心词转化为独热码

上下文处理：将上下文单词转化为各单词独热码的均值

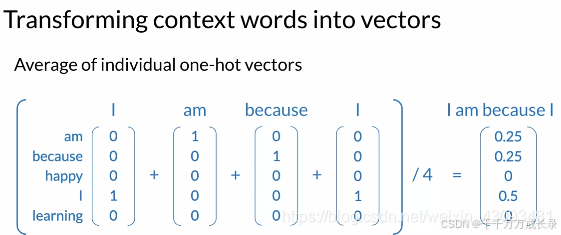
训练集处理：将处理好数据构成如下格式

4.连续词袋模型(Continuous Bag-of-Words Model，CBOW)

4.1 基本概念

定义：是基于机器学习的词嵌入方法，根据上下文来预测中心词，由此构建出词嵌入向量

基本原理：通过预测中心词能很大程度表示其语义，因为一个词出现在句子中时，通常都有相似的上下文，由此可判断上下文间存在语义联系

CBOW训练流程：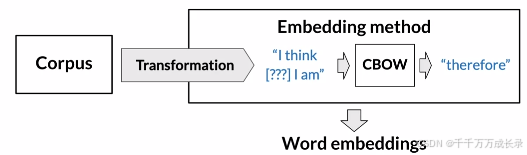

4.2 CBOW结构

结构：包含输入层、隐藏层、输出层；是浅层神经网络

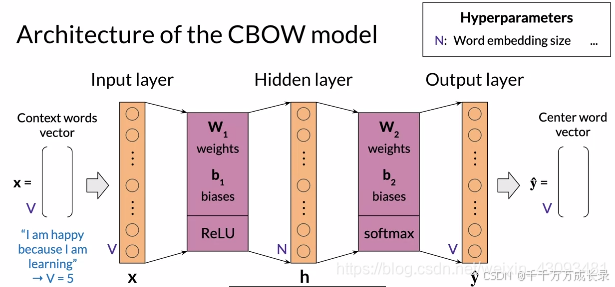
各层的维度：

输入单个数据时：

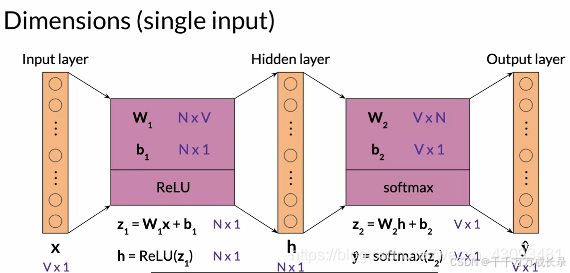
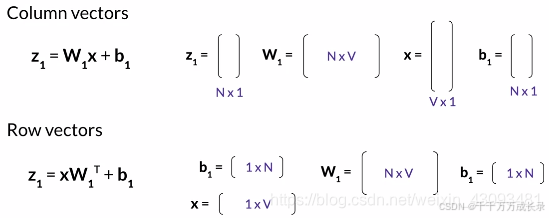
输入批量数据时：

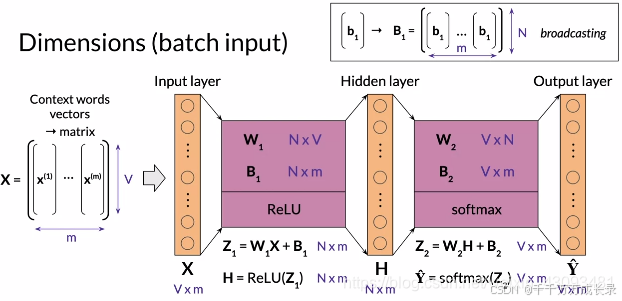
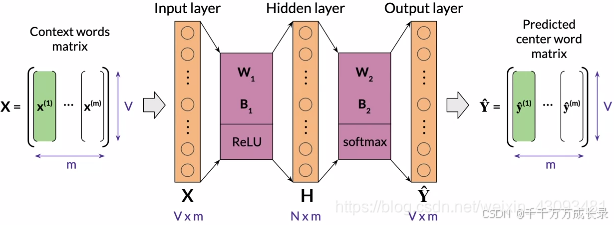
4.3 激活函数
ReLU： Softmax

例：

4.4 损失函数

流程：

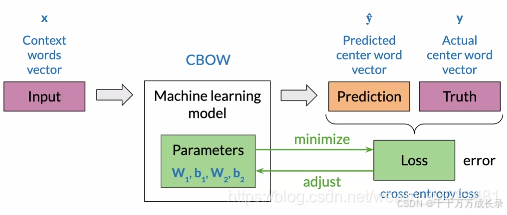
交叉熵损失函数(Cross-entropy loss)：

功能：计算真实中心词和预测中心词之间的差异

评价：若预测正确则损失值小，反之损失值大

4.5 正向传播

计算损失值：定义：一个batch训练数据的loss的平均值，即为损失值

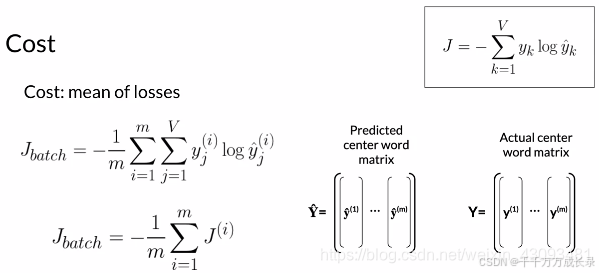
4.6 反向传播

最小化损失值：

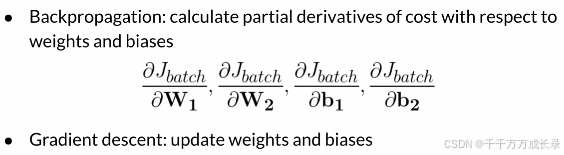
反向传播：

梯度下降：略

5.词嵌入的提取与评估

5.1 词嵌入提取

方法1：用W1，即第一个隐藏层参数作为词嵌入

方法2：用W2，即第二个隐藏层参数作为词嵌入

方法3：用W1和W2取平均，即用两个隐藏层参数的平均值作为词嵌入

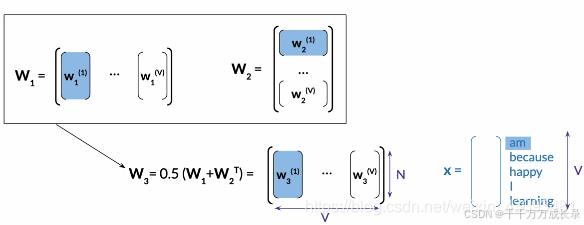
5.2 词嵌入评估

内部评估：

定义：不需要外部数据，直接评估词嵌入对于单词之间语义或语法捕捉能力的好坏

方法：

(1)类比测试：通过构建一系列类比(找同义词)的任务，来评价词嵌入好坏

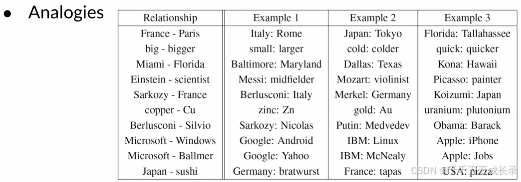
(2)直观判断：通过聚类和可视化处理，直观判断词嵌入对语义的捕获能力

聚类可视化：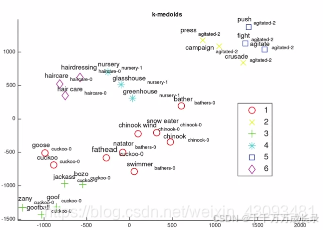

外部评估：

方法：应用训练好的词嵌入进行其他任务，如命名实体识别、词性标注等，通过在这些任务上的表现来体现词嵌入的好坏

优点：能直接评价词嵌入在实际任务上的表现

缺点：耗时大、更难以分析问题

原文链接：https://blog.youkuaiyun.com/weixin_43093481/article/details/115362897

情感分析测试句子表达的情绪选择RNN循环神经网络

通过输入当前单词的xt，和上一个隐藏层状态ht−1，来生成下一个隐藏层状态ht

用公式表示为：ht=RNN(xt,ht−1) 一旦当我们获得了最后一个隐藏层的输出：hT（通过输入最后一个单词序列xT和前一个隐藏层状态hT−1获得），就可以将它输入一个线性层f（也称为全连接层），得到最终的情绪预测结果：y^=f(hT).

为什么只在训练集上建立词汇表？因为在测试模型时，都不能以任何方式影响测试集。当然也不包括验证集，因为希望验证集尽可能地反映测试集。

import torch
from torchtext.legacy import data
# 设置随机种子数，该数可以保证随机数是可重复的
SEED = 1234
# 设置种子
torch.manual_seed(SEED)
torch.backends.cudnn.deterministic = True
# 读取数据和标签
TEXT = data.Field(tokenize = 'spacy', tokenizer_language = 'en_core_web_sm')
LABEL = data.LabelField(dtype = torch.float)

from torchtext.legacy import datasets
train_data, test_data = datasets.IMDB.splits(TEXT, LABEL)

print(f'Number of training examples: {len(train_data)}')
print(f'Number of testing examples: {len(test_data)}')
print(vars(train_data.examples[0]))

import random
train_data, valid_data = train_data.split(split_ratio=0.8 , random_state = random.seed(SEED))  #再把训练集划分为训练集和测试集

print(f'Number of training examples: {len(train_data)}')
print(f'Number of validation examples: {len(valid_data)}')
print(f'Number of testing examples: {len(test_data)}')

MAX_VOCAB_SIZE = 25000
TEXT.build_vocab(train_data, max_size = MAX_VOCAB_SIZE)
LABEL.build_vocab(train_data) #构建词汇表

print(f"Unique tokens in TEXT vocabulary: {len(TEXT.vocab)}")
print(f"Unique tokens in LABEL vocabulary: {len(LABEL.vocab)}")
print(TEXT.vocab.freqs.most_common(20))

这些都是它自己包含的方法吗名字都好通俗易懂！ freq—频率；most_common—最大出现次数’

#使用 stoi (string to int) or itos (int to string) 方法，以下输出text-vocab的前10个词汇。

print(TEXT.vocab.itos[:10])

BATCH_SIZE = 64

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

train_iterator, valid_iterator, test_iterator = data.BucketIterator.splits(
    (train_data, valid_data, test_data), 
    batch_size = BATCH_SIZE,
    device = device)

import torch.nn as nn

class RNN(nn.Module):
    def __init__(self, input_dim, embedding_dim, hidden_dim, output_dim):
        
        super().__init__()
        
        self.embedding = nn.Embedding(input_dim, embedding_dim)
        
        self.rnn = nn.RNN(embedding_dim, hidden_dim)
        
        self.fc = nn.Linear(hidden_dim, output_dim)
        
    def forward(self, text):

        #text = [sent len, batch size]
        
        embedded = self.embedding(text)
        
        #embedded = [sent len, batch size, emb dim]
        
        output, hidden = self.rnn(embedded) #？
        
        #output = [sent len, batch size, hid dim]
        #hidden = [1, batch size, hid dim]
        
        assert torch.equal(output[-1,:,:], hidden.squeeze(0))
        
        return self.fc(hidden.squeeze(0))

squeeze 方法, 可以消除维度为1的维度

下面，我们可以做建立一个RNN的例子

输入维度就是对应one-hot向量的维度, 也等同于词典的维度.

embedding 维度是可以设置的超参数. 通常设置为 50-250 维度, 某种程度上也和词典大小有关.

隐藏层维度就是最后一层隐藏层的大小. 通常可以设置为100-500维, 这个也会词典大小，任务的复杂程度都有关系

输出的维度就是要分类的类别的数目。

INPUT_DIM = len(TEXT.vocab)
EMBEDDING_DIM = 100
HIDDEN_DIM = 256
OUTPUT_DIM = 1

model = RNN(INPUT_DIM, EMBEDDING_DIM, HIDDEN_DIM, OUTPUT_DIM)

也可以输出要训练的参数数目看看.

def count_parameters(model):
    return sum(p.numel() for p in model.parameters() if p.requires_grad)

print(f'The model has {count_parameters(model):,} trainable parameters')

The model has 2,592,105 trainable parameters

1.4 训练模型

在模型训练前，先要设置优化器，这里我们选择的是SGD，随机梯度下降计算，model.parameters()表示需要更新的参数，lr为学习率

import torch.optim as optim

optimizer = optim.SGD(model.parameters(), lr=1e-3)

接下来定义损失函数，BCEWithLogitsLoss一般用来做二分类。

criterion = nn.BCEWithLogitsLoss()

用 .to, 可以将张量放到gpu上计算。

model = model.to(device)
criterion = criterion.to(device)

损失函数用来计算损失值，还需要计算准确率的函数。

将sigmoid层输出的预测结果输入到计算准确率的函数, 取整到最近的整数.大于0.5，就取1。反之取0。

计算出预测的结果和label一致的值，在除以所有的值，就可以得到准确率。

def binary_accuracy(preds, y):
    """
    Returns accuracy per batch, i.e. if you get 8/10 right, this returns 0.8, NOT 8
    """

    #round predictions to the closest integer
    rounded_preds = torch.round(torch.sigmoid(preds))
    correct = (rounded_preds == y).float() #convert into float for division 
    acc = correct.sum() / len(correct)
    return acc

train 函数迭代所有的样本，每次都是一个batch。

model.train() 将model处于 "training 模式", 也会打开 dropout 和 batch normalization. 在每一次的batch, 先将梯度清0. 模型的每一个参数都有一个 grad 属性，存储着损失函数计算的梯度值. PyTorch 不会自动删除（或“归零”）从上次梯度计算中计算出的梯度，因此必须手动将其归零。

每次输入, batch.text, 到模型中. 只需要调用模型即可.

用loss.backward()计算梯度，更新参数使用的是 optimizer.step()。

损失值和准确率在整个 epoch 中累积, .item()抽取张量中只含有一个值的张量中的值。

最后，我们返回损失和准确率，在整个 epoch 中取平均值. len可以得到epoch中的batch数

当然在计算的时候，要记得将LongTensor转化为 torch.float。这是因为 TorchText 默认将张量设置为 LongTensor。

def train(model, iterator, optimizer, criterion):
    
    epoch_loss = 0
    epoch_acc = 0
    
    model.train()
    
    for batch in iterator:
        
        optimizer.zero_grad()
                
        predictions = model(batch.text).squeeze(1)
        
        loss = criterion(predictions, batch.label)
        
        acc = binary_accuracy(predictions, batch.label)
        
        loss.backward()
        
        optimizer.step()
        
        epoch_loss += loss.item()
        epoch_acc += acc.item()
        
    return epoch_loss / len(iterator), epoch_acc / len(iterator)

evaluate 和 train相似, 只要将train函数稍微进行修改即可。

model.eval() 将模型置于"evaluation 模式", 这会关掉 dropout 和 batch normalization.

在with no_grad() 下，不会进行梯度计算. 这会导致使用更少的内存并加快计算速度.

其他函数在train中类似,在evaluate中移除了 optimizer.zero_grad(), loss.backward() and optimizer.step(), 因为不再需要更新参数了

def evaluate(model, iterator, criterion):
    
    epoch_loss = 0
    epoch_acc = 0
    
    model.eval()
    
    with torch.no_grad():
    
        for batch in iterator:

            predictions = model(batch.text).squeeze(1)
            
            loss = criterion(predictions, batch.label)
            
            acc = binary_accuracy(predictions, batch.label)

            epoch_loss += loss.item()
            epoch_acc += acc.item()
        
    return epoch_loss / len(iterator), epoch_acc / len(iterator)

接下来创建计算每一个epoch会消耗多少时间的函数。

import time

def epoch_time(start_time, end_time):
    elapsed_time = end_time - start_time
    elapsed_mins = int(elapsed_time / 60)
    elapsed_secs = int(elapsed_time - (elapsed_mins * 60))
    return elapsed_mins, elapsed_secs

然后，我们通过多个 epoch 来训练模型，每一个 epoch 是对训练和验证集中所有样本的完整传递。

在每个epoch，如果在验证集上的损失值是迄今为止我们所见过的最好的，我们将保存模型的参数，然后在训练完成后我们将在测试集上使用该模型。

N_EPOCHS = 5

best_valid_loss = float('inf')

for epoch in range(N_EPOCHS):

    start_time = time.time()
    
    train_loss, train_acc = train(model, train_iterator, optimizer, criterion)
    valid_loss, valid_acc = evaluate(model, valid_iterator, criterion)
    
    end_time = time.time()

    epoch_mins, epoch_secs = epoch_time(start_time, end_time)
    
    if valid_loss < best_valid_loss:
        best_valid_loss = valid_loss
        torch.save(model.state_dict(), 'tut1-model.pt')
    
    print(f'Epoch: {epoch+1:02} | Epoch Time: {epoch_mins}m {epoch_secs}s')
    print(f'\tTrain Loss: {train_loss:.3f} | Train Acc: {train_acc*100:.2f}%')
    print(f'\t Val. Loss: {valid_loss:.3f} |  Val. Acc: {valid_acc*100:.2f}%')

Epoch: 01 | Epoch Time: 0m 17s
	Train Loss: 0.694 | Train Acc: 50.12%
	 Val. Loss: 0.696 |  Val. Acc: 50.17%
Epoch: 02 | Epoch Time: 0m 16s
	Train Loss: 0.693 | Train Acc: 49.72%
	 Val. Loss: 0.696 |  Val. Acc: 51.01%
Epoch: 03 | Epoch Time: 0m 16s
	Train Loss: 0.693 | Train Acc: 50.22%
	 Val. Loss: 0.696 |  Val. Acc: 50.87%
Epoch: 04 | Epoch Time: 0m 16s
	Train Loss: 0.693 | Train Acc: 49.94%
	 Val. Loss: 0.696 |  Val. Acc: 49.91%
Epoch: 05 | Epoch Time: 0m 17s
	Train Loss: 0.693 | Train Acc: 50.07%
	 Val. Loss: 0.696 |  Val. Acc: 51.00%

如上所示，损失并没有真正减少多少，而且准确性很差。这是由于这是baseline，我们将在下一个notbook中改进的模型的几个问题。

最后，要得到真正关心的指标，测试集上的损失和准确性，参数将从已经训练好的模型中获得，这些参数为我们提供了最好的验证集上的损失。

model.load_state_dict(torch.load('tut1-model.pt'))

test_loss, test_acc = evaluate(model, test_iterator, criterion)

print(f'Test Loss: {test_loss:.3f} | Test Acc: {test_acc*100:.2f}%')

Test Loss: 0.708 | Test Acc: 47.87%

GPU（图形处理器）和CPU（中央处理器）

是计算机系统中两种关键的处理单元，它们在多个方面存在显著差异，这些差异主要体现在功能、架构、计算方式以及应用场景上。

1. 功能与用途

CPU：作为计算机系统的核心处理器，CPU负责执行程序的指令和控制计算机的各个部件。它擅长处理多样化的任务，包括计算、逻辑操作、控制以及输入输出操作。CPU的设计更加通用，适用于广泛的计算任务，如操作系统、应用程序、编译器等。此外，CPU还用于服务器、数据库、虚拟化等需要高度可靠性和灵活性的应用。
GPU：GPU最初设计用于处理图形和图像渲染任务，但近年来已扩展到其他需要大量并行计算的领域。GPU具有强大的并行处理能力，能够同时执行多个相似的计算任务。它在图形渲染、深度学习、科学计算等领域具有出色的性能。例如，在游戏开发中，GPU用于实现逼真的图形效果和物理模拟；在深度学习中，GPU加速神经网络的训练和推理过程。

2. 架构与核心数量

CPU：通常具有较少的核心数（例如4到16个核心），但每个核心都非常强大，能够处理复杂的指令和任务。CPU的核心具有复杂的控制单元，能够高效地处理复杂的指令和任务调度。此外，CPU还拥有大容量的缓存（如L1、L2、L3缓存），用于加速数据访问和指令执行。
GPU：则拥有大量的核心（通常为数百到数千个），但每个核心相对较弱。GPU采用单指令多数据（SIMD）架构，适合并行处理大规模的数据。GPU的核心数量多，但每个核心的频率较低，这使得它能够在同一时间内处理多个简单的计算任务。

3. 计算方式

CPU：主要通过顺序执行指令来完成计算任务。它按照程序设定的顺序，一条一条地执行指令，这种计算方式被称为串行计算。串行计算使得CPU能够精确地控制程序的执行流程，适用于需要复杂逻辑和精确控制的应用场景。
GPU：则采用并行计算的方式来处理任务。GPU能够同时执行大量的线程，这些线程被分配到不同的流处理器上进行处理。并行计算使得GPU在处理大规模数据和执行重复计算任务时具有极高的效率。

4. 应用场景

CPU：由于其通用性和强大的单核性能，CPU在广泛的应用领域中发挥作用。它适用于日常计算任务，如办公软件、网页浏览、多媒体播放等。此外，CPU还用于需要复杂逻辑和精确控制的应用场景，如数据库管理、虚拟化等。
GPU：由于其并行计算能力，GPU在图形处理和科学计算领域得到广泛应用。例如，在游戏开发中，GPU用于实现高质量的图形渲染；在深度学习中，GPU加速神经网络的训练和推理过程；在科学计算中，GPU用于处理大规模数据和执行复杂的计算任务。