双线性插值

1、为什么要用图像的插值？

       在图像的放大和缩小的过程中，需要计算新图像像素点在原图的位置，如果计算的位置不是整数，就需要用到图像的内插，我们需要寻找在原图中最近得像素点赋值给新的像素点，这种方法很简单是最近邻插法，这种方法好理解、简单，但是不实用，会产生是真现象，产生棋盘格效应，更实用的方法就是双线性内插。

2、一维线性插值

我们已经知道（x0，y0）与（x1, y1）的值，并且已知 x 的值，要求 y 的值。根据初中的知识：

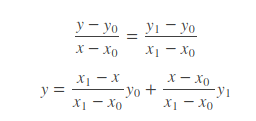
3、双线性插值

       双线性插值，又称为双线性内插。在数学上，双线性插值是有两个变量的插值函数的线性插值扩展，其核心思想是在两个方向分别进行一次线性插值。

        假如我们想得到未知函数  在点 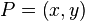 的值，假设我们已知函数  在 , , , 及  四个点的值。

     首先在 x 方向进行线性插值，得到

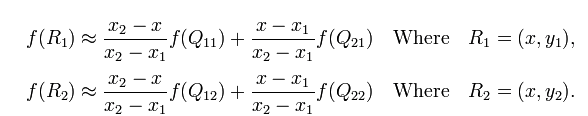
然后在 y 方向进行线性插值，得到

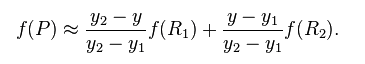
这样就得到所要的结果 ：

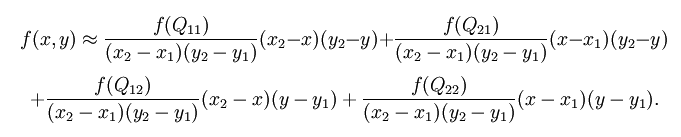
果选择一个坐标系统使得  的四个已知点坐标分别为 (0, 0)、(0, 1)、(1, 0) 和 (1, 1)，那么插值公式就可以化简为：

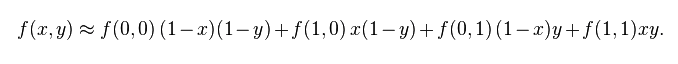
或者用矩阵运算表示为:

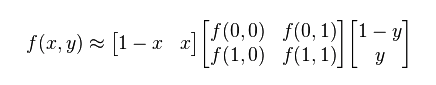
      与这种插值方法名称不同的是，这种插值方法的结果通常不是线性的，它的形式是：

     常数的数目都对应于给定的 f 的数据点数目：

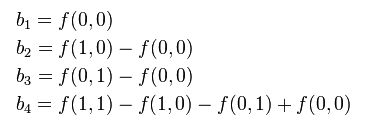
线性插值的结果与插值的顺序无关。首先进行 y 方向的插值，然后进行 x 方向的插值，所得到的结果是一样的。

其中上面的公式的推倒过程如下：