深度学习入门笔记之ALexNet网络

Alex提出的alexnet网络结构模型，在imagenet2012图像分类challenge上赢得了冠军。作者训练alexnet网络时大致将120万张图像的训练集循环了90次，在两个NVIDIA GTX 580 3GB GPU上花了五到六天。
来源论文：Krizhevsky, Alex, Ilya Sutskever, and Geoffrey E. Hinton. “Imagenet classification with deep convolutional neural networks.” Advances in neural information processing systems. 2012.”

一 AlexNet创新点：

1 使用Relu替换之前的sigmoid的作为激活函数
2 使用了数据增强策略（Data Augmentation），抑制过拟合
3 使用了重叠的最大池化（Max Pooling）。此前的CNN通常使用平均池化，而AlexNet全部使用最大池化，成功避免了平均池化带来的模糊化效果
4 提出LRN（局部响应归一化）
5 成功使用Dropout机制，抑制过拟合
6 多GPU训练

详细介绍如下：
1 ReLu作为激活函数
在最初的感知机模型中，输入和输出的关系如下：

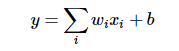
只是单纯的线性关系，这样的网络结构有很大的局限性：即使用很多这样结构的网络层叠加，其输出和输入仍然是线性关系，无法处理有非线性关系的输入输出。因此，对每个神经元的输出做个非线性的转换也就是，将上面就加权求和的结果输入到一个非线性函数，也就是激活函数中。 这样，由于激活函数的引入，多个网络层的叠加就不再是单纯的线性变换，而是具有更强的表现能力。在最初，sigmoid和tanh函数最常用的激活函数。

**sigmoid：**在网络层数较少时，sigmoid函数的特性能够很好的满足激活函数的作用。它把一个实数压缩至0到1之间，当输入的数字非常大的时候，结果会接近1；当输入非常大的负数时，则会得到接近0的结果。这种特性，能够很好的模拟神经元在受刺激后，是否被激活向后传递信息（输出为0，几乎不被激活；输出为1，完全被激活）。
sigmoid一个很大的问题就是梯度饱和。 观察sigmoid函数的曲线，当输入的数字较大（或较小）时，其函数值趋于不变，其导数变的非常的小。这样，在层数很多的的网络结构中，进行反向传播时，由于很多个很小的sigmoid导数累成，导致其结果趋于0，权值更新较慢。

**ReLu：**针对sigmoid梯度饱和导致训练收敛慢的问题，在AlexNet中引入了ReLU。ReLU是一个分段线性函数，小于等于0则输出为0；大于0的则恒等输出。相比于sigmoid，ReLU有以下特点：
（1）计算开销小。sigmoid的正向传播有指数运算，倒数运算，而ReLu是线性输出；反向传播中，sigmoid有指数运算，而ReLU有输出的部分，导数始终为1。
（2）梯度饱和问题
（3）稀疏性。Relu会使一部分神经元的输出为0，这样就造成了网络的稀疏性，并且减少了参数的相互依存关系，缓解了过拟合问题的发生。

这里有个问题，前面提到，激活函数要用非线性的，是为了使网络结构有更强的表达的能力。那这里使用ReLU本质上却是个线性的分段函数，是怎么进行非线性变换的。
这里把神经网络看着一个巨大的变换矩阵M，其输入为所有训练样本组成的矩阵A，输出为矩阵B。这里的M是一个线性变换的话，则所有的训练样本A进行了线性变换输出为B。

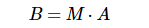
那么对于ReLU来说，由于其是分段的，0的部分可以看做神经元没有激活，不同的神经元激活或者不激活，其神经元组成的变换矩阵是不一样的。
设有两个训练样本 a1,a2，其训练时神经网络组成的变换矩阵为M1,M2。 由于M1变换对应的神经网络中激活神经元和M2是不一样的，这样M1,M2实际上是两个不同的线性变换。也就是说，每个训练样本使用的线性变换矩阵Mi是不一样的，在整个训练样本空间来说，其经历的是非线性变换。
简单来说，不同训练样本中的同样的特征，在经过神经网络学习时，流经的神经元是不一样的（激活函数值为0的神经元不会被激活）。这样，最终的输出实际上是输入样本的非线性变换。单个训练样本是线性变换，但是每个训练样本的线性变换是不一样的，这样整个训练样本集来说，就是非线性的变换。
传统神经网络激活函数通常为反正切或是sigmoid，AlexNet使用RELU作为激活函数，相比于反正切，该方法训练速度大约有6倍提升。RELU激活函数简单到难以置信。

2 数据增强
神经网络由于训练的参数多，需要比较多的数据量，不然很容易过拟合。当训练数据有限时，可以通过一些变换从已有的训练数据集中生成一些新的数据，以快速地扩充训练数据。对于图像数据集来说，可以对图像进行一些形变操作：
（1）翻转
（2）随机裁剪
（3）平移，颜色光照的变换
AlexNet中对数据做了以下操作：
（1）随机裁剪，对256×256的图片进行随机裁剪到227×227，然后进行水平翻转。
（2）测试的时候，对左上、右上、左下、右下、中间分别做了5次裁剪，然后翻转，共10个裁剪，之后对结果求平均。
（3）对RGB通道使用了PCA（主成分分析），对每个训练图片的每个像素，提取出RGB三个通道的特征向量与特征值，对每个特征值乘以一个α，α是一个均值0.1方差服从高斯分布的随机变量。也就是对颜色、光照作变换，结果使错误率又下降了1%。

3 层叠池化
在LeNet中池化是不重叠的，即池化的窗口的大小和步长是相等的，如下：

在AlexNet中使用的池化（Pooling）却是可重叠的，也就是说，在池化的时候，每次移动的步长小于池化的窗口长度。AlexNet池化的大小为3×3的正方形，每次池化移动步长为2，这样就会出现重叠。重叠池化可以避免过拟合，这个策略贡献了0.3%的Top-5错误率。与非重叠方案s=2，z=2s=2，z=2相比，输出的维度是相等的，并且能在一定程度上抑制过拟合。

4 局部响应归一化
ReLU具有让人满意的特性，它不需要通过输入归一化来防止饱和。如果至少一些训练样本对ReLU产生了正输入，那么那个神经元上将发生学习。然而，我们仍然发现接下来的局部响应归一化有助于泛化。a(x,y)(i)表示神经元激活，通过在(x,y)位置应用核i，然后应用ReLU非线性来计算，响应归一化激活b(x,y)(i)通过下式给定：

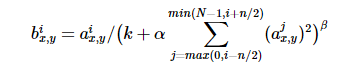
其中，N是卷积核的个数，也就是生成的FeatureMap的个数；k,α,β,n是超参数，论文中使用的值是k=2,n=5,α=10(-4),β=0.75。

输出b(x,y)(i)和输入a(x,y)(j)的上标表示的是当前值所在的通道，也即是叠加的方向是沿着通道进行。将要归一化的值a(x,y)(i)所在附近通道相同位置的值的平方累加起来

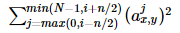
Hinton等人认为LRN层模仿生物神经系统的侧抑制机制，对局部神经元的活动创建竞争机制，使得响应比较大的值相对更大，提高模型泛化能力。但是，后来的论文比如Very Deep Convolution Networks for Large-Scale Image Recognition（也就是提出VGG网络的文章）中证明，LRN对CNN并没有什么作用，反而增加了计算复杂度，因此，这一技术也不再使用了。

5 Dropout
这个是比较常用的抑制过拟合的方法了。
引入Dropout主要是为了防止过拟合。在神经网络中Dropout通过修改神经网络本身结构来实现，对于某一层的神经元，通过定义的概率将神经元置为0，这个神经元就不参与前向和后向传播，就如同在网络中被删除了一样，同时保持输入层与输出层神经元的个数不变，然后按照神经网络的学习方法进行参数更新。在下一次迭代中，又重新随机删除一些神经元（置为0），直至训练结束。
Dropout应该算是AlexNet中一个很大的创新，现在神经网络中的必备结构之一。Dropout也可以看成是一种模型组合，每次生成的网络结构都不一样，通过组合多个模型的方式能够有效地减少过拟合，Dropout只需要两倍的训练时间即可实现模型组合（类似取平均）的效果，非常高效。
如下图：

在AlexNet中，在训练时，每层的keep_prob被设置为0.5，而在测试时，所有的keep_prob都为1.0，也即关闭dropout，并把所有神经元的输出均乘以0.5，保证训练时和测试时输出的均值接近。当然，dropout只用于全连接层。没有dropout，AlexNet网络将会遭遇严重的过拟合，加入dropout后，网络的收敛速度慢了接近一倍。

二 AlexNet网络结构

AlexNet和LeNet -5-网络有些许不同，在LeNet-5网络里，卷积层和池化层是分开的，即一层卷积层一层池化这样分布的，但是AlexNet网络卷积和池化层合为一体了，而且还是分两路设计网络。

（一）总体概述下：
（1）AlexNet为8层结构，其中前5层为卷积层，后面3层为全连接层；学习参数有6千万个，神经元有650,000个。
（2）AlexNet在两个GPU上运行。
（3）AlexNet在第2,4,5层均是前一层自己GPU内连接，第3层是与前面两层全连接，全连接是2个GPU全连接。
（4）LRN层第1,2个卷积层后。
（5）Max pooling层在LRN层以及第5个卷积层后。
（6）ReLU在每个卷积层以及全连接层后。
（7）Dropout层减少过度拟合，应用在前两个全连接层。
（二）详解各层训练参数的计算：
前五层：卷积层

后三层：全连接层

整体计算图：

（三）详解AlexNet网络的各层：
卷积层C1
该层的处理流程是： 卷积–>ReLU–>池化–>归一化。
（1）卷积，输入是227×227*3，使用96个11×11×3（卷积核最后一个的维数一定与输入最后一个的维数相同）的卷积核，得到的FeatureMap为55×55×96。
（2）ReLU，将卷积层输出的FeatureMap输入到ReLU函数中。
（3）池化，使用3×3步长为2的池化单元（重叠池化，步长小于池化单元的宽度），输出为27×27×96（(55−3)/2+1=27。
（4）局部响应归一化，使用k=2,n=5,α=10(−4),β=0.75进行局部归一化，输出的仍然为27×27×96，输出分为两组，每组的大小为27×27×48。

卷积层C2
该层的处理流程是：卷积–>ReLU–>池化–>归一化
（1）卷积，输入是2组27×27×48。使用2组，每组128个尺寸为5×5×48的卷积核，并作了边缘填充padding=2，卷积的步长为1. 则输出的FeatureMap为2组，每组的大小为27×27 times128。（(27+2∗2−5)/1+1=27
（2）ReLU，将卷积层输出的FeatureMap输入到ReLU函数中。
（3）池化运算的尺寸为3×3，步长为2，池化后图像的尺寸为(27−3)/2+1=13，输出为13×13×256。
（4）局部响应归一化，使用k=2,n=5,α=10(−4),β=0.75进行局部归一化，输出的仍然为13×13×256，输出分为2组，每组的大小为13×13×128。

卷积层C3
该层的处理流程是： 卷积–>ReLU
（1）卷积，输入是13×13×256，使用2组共384尺寸为3×3×256的卷积核，做了边缘填充padding=1，卷积的步长为1。则输出的FeatureMap为13×13×384。
（2）ReLU，将卷积层输出的FeatureMap输入到ReLU函数中。

卷积层C4
该层的处理流程是： 卷积–>ReLU
该层和C3类似。
（1）卷积，输入是13×13×384，分为两组，每组为13×13×192。使用2组，每组192个尺寸为3×3×192的卷积核，做了边缘填充padding=1，卷积的步长为1。则输出的FeatureMap为13×13 times384，分为两组，每组为13×13×192。
（2）ReLU，将卷积层输出的FeatureMap输入到ReLU函数中。

卷积层C5
该层处理流程为：卷积–>ReLU–>池化
（1）卷积，输入为13×13×384，分为两组，每组为13×13×192。使用2组，每组为128尺寸为3×3×192的卷积核，做了边缘填充padding=1，卷积的步长为1。则输出的FeatureMap为13×13×256。
（2）ReLU，将卷积层输出的FeatureMap输入到ReLU函数中。
（3）池化，池化运算的尺寸为3×3，步长为2，池化后图像的尺寸为 (13−3)/2+1=6,即池化后的输出为6×6×256。

全连接层FC6
该层的流程为：（卷积）全连接 -->ReLU -->Dropout
（1）卷积->全连接： 输入为6×6×256,该层有4096个卷积核，每个卷积核的大小为6×6×256。由于卷积核的尺寸刚好与待处理特征图（输入）的尺寸相同，即卷积核中的每个系数只与特征图（输入）尺寸的一个像素值相乘，一一对应，因此，该层被称为全连接层。由于卷积核与特征图的尺寸相同，卷积运算后只有一个值，因此，卷积后的像素层尺寸为4096×1×1，即有4096个神经元。
（2）ReLU,这4096个运算结果通过ReLU激活函数生成4096个值。
（3）Dropout,抑制过拟合，随机的断开某些神经元的连接或者是不激活某些神经元。

全连接层FC7
流程为：全连接–>ReLU–>Dropout
（1）全连接，输入为4096的向量。
（2）ReLU,这4096个运算结果通过ReLU激活函数生成4096个值。
（3）Dropout,抑制过拟合，随机的断开某些神经元的连接或者是不激活某些神经元。

输出层
第七层输出的4096个数据与第八层的1000个神经元进行全连接，经过训练后输出1000个float型的值，这就是预测结果。

AlexNet参数数量
卷积层的参数 = 卷积核的数量 * 卷积核 + 偏置

C1: 96个11×11×3的卷积核，96×11×11×3+96=34848

C2: 2组，每组128个5×5×48的卷积核，(128×5×5×48+128)×2=307456

C3: 384个3×3×256的卷积核，3×3×256×384+384=885120

C4: 2组，每组192个3×3×192的卷积核，(3×3×192×192+192)×2=663936

C5: 2组，每组128个3×3×192的卷积核，(3×3×192×128+128)×2=442624

FC6: 4096个6×6×256的卷积核，6×6×256×4096+4096=37752832

FC7: 4096∗4096+4096=16781312

output: 4096∗1000=4096000

卷积层 C2,C4,C5中的卷积核只和位于同一GPU的上一层的FeatureMap相连。从上面可以看出，参数大多数集中在全连接层，在卷积层由于权值共享，权值参数较少。

（四）Details of Learning 学习中的细节
（1）输入是224×224224×224，不过经过计算(224−11)/4=54.75并不是论文中的55×55，而使用227×227作为输入，则(227−11)/4=55。

（2）输入的图片的像素是224x224的且有三层，这三层代表三原色RGB（我们知道所谓的彩色其实就是三原色组合而成的，因此彩色图片也是这样），我们可以简单的看做有三张图片堆叠而成的彩色图片，这三张图片分别对应红色，绿色，蓝色，在LeNet -5-网络只有一层，因为颜色是灰度的。输入层的采样窗口为11×11且也有三层对应图片的三层，那么每采样一次有多少个连接呢？有11x11x3 = 363个，采样窗口的平移步长是4，（在LeNet -5-网络移动步长是1，这里是4，应该很容易理解）为什么步长是4而不是1呢？因为考虑到计算量的问题，如果是1步计算量太大。那么这样的采样窗口在图像上采样后的维度是多少呢？

（3）AlexNet使用了mini-batch SGD，batch的大小为128，梯度下降的算法选择了momentum，参数为0.9，加入了L2正则化，或者说权重衰减，参数为0.0005。论文中提到，这么小的权重衰减参数几乎可以说没有正则化效果，但对模型的学习非常重要。

（4）每一层权重均初始化为0均值0.01标准差的高斯分布，在第二层、第四层和第五层卷积的偏置被设置为1.0，而其他层的则为0，目的是为了加速早期学习的速率（因为激活函数是ReLU，1.0的偏置可以让大部分输出为正）。

（5）对于所有层都使用了相等的学习率，这是在整个训练过程中手动调整的。学习速率初始值为0.01，在训练结束前共减小3次，每次减小都出现在错误率停止减少的时候，每次减小都是把学习速率除以10 。

（6）深度很重要，去掉任一层，性能都会降低。

（7）为了简化实验，没有使用非监督预训练。但是当有足够计算能力扩大网络结构，而没增加相应数据时，非监督预训练可能会有所帮助。

三 代码实现（Pytorch）

主要参考 https://www.bilibili.com/video/BV1W7411T7qc
这部分搭建AlexNet网络并训练花分类数据集。
1 数据集下载。
http://download.tensorflow.org/example_images/flower_photos.tgz
包含 5 中类型的花，每种类型有600~900张图像不等。将flower_photos拷贝到flower_data文件夹下，并解压缩。
2 对数据集进行划分，划分为训练集与验证集。
由于此数据集不像 CIFAR10 那样下载时就划分好了训练集和测试集，因此需要自己划分。split_data.py会按照9:1的比例将数据集分为训练集和验证集。
在split_data.py的当前页面，shift + 右键 打开 PowerShell 窗口，输入 python split_data.py，就会自动进行转换了。

划分以后的数据集目录如下：

|-- flower_data
	|-- flower_photos
		|-- daisy
		|-- dandelion
		|-- roses
		|-- sunflowers
		|-- tulips
		|-- LICENSE.txt
	|-- train
		|-- daisy
		|-- dandelion
		|-- roses
		|-- sunflowers
		|-- tulips
	|-- val
		|-- daisy
		|-- dandelion
		|-- roses
		|-- sunflowers
		|-- tulips
	|-- flower_photos.tgz
|-- flower_link.txt
|-- README.md
|-- split_data.py

3 注释model.py。

import torch.nn as nn
import torch

class AlexNet(nn.Module):
    def __init__(self, num_classes=1000, init_weights=False):
        super(AlexNet, self).__init__()
        #与LeNet不一样的地方
        #用nn.Sequential模块，可以将一系列的层结构进行打包，组合成一个新的结构，在这里取名叫features
        self.features = nn.Sequential(
            #padding可以传入整形或者tuple(1,2)。如果传入整形1，那就会在特征矩阵的上下各补一行零，左右两侧各补一列零。
            # tuple(1,2)表示上下各补一行零，左右两侧各补两列零
            #如果想更精确，就要用官网的nn.ZeroPad2d（（1,2,1,2）），左侧补一列，右侧补两列，上方补一行，下方补两行
            nn.Conv2d(3, 48, kernel_size=11, stride=4, padding=2),  # input[3, 224, 224]  output[48, 55, 55]
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=3, stride=2),                  # output[48, 27, 27]
            nn.Conv2d(48, 128, kernel_size=5, padding=2),           # output[128, 27, 27]
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=3, stride=2),                  # output[128, 13, 13]
            nn.Conv2d(128, 192, kernel_size=3,