【玩转机械臂】（一）机器人学的数学基础：坐标变换与位姿描述

笔者注：这是【玩转机械臂】专栏的第（一）篇文章，内容主体来源于笔者近期的学习与思考。作为持续学习的过程，笔者亦是抱着“边学边写”的态度，以做笔记的方式记录下专业领域的相关知识，愿能为更多处于学习或研究初期志同道合的朋友提供参考，文中如有疏漏之处，恳请广大前辈和读者批评指正。文末将附上有前后衔接关系的相应文章链接，欢迎跳转查看。

机器人学 (Robotics) 是研究机械臂、机器狗、无人车、旋翼无人机乃至人形机器人的最重要的基础。尽管当前深度学习、强化学习等数据驱动的无模型算法乃至VLA等端到端学习方法已逐渐成为趋势，但对于希望深入理解机器人本质的初学者而言，扎实掌握最“原始”也最经典的机器人学理论依然是不可或缺的。本系列将以若干本经典的教材和理论专著为基础，系统地梳理机器人学相关知识，并以当前工业界常用的多自由度机械臂为主要研究对象，对机器人控制领域常见的一些方法和理念作简要的阐述。

本文将首先总结梳理机器人学所需的数学基础。

考虑不同的坐标系{A}{B}中同一点M的坐标，分别记为3维列向量：

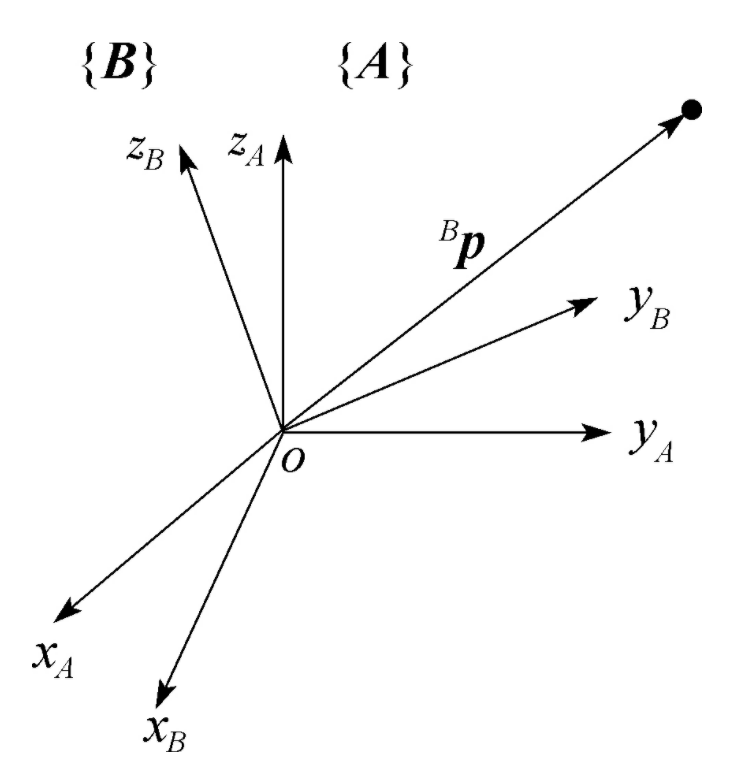
$^A\boldsymbol{p}_M=\begin{bmatrix} ^Ax_{M} \\ ^Ay_{M} \\ ^Az_{M} \end{bmatrix}$ , $^B\boldsymbol{p}_M=\begin{bmatrix} ^Bx_{M} \\ ^By_{M} \\ ^Bz_{M} \end{bmatrix}$

此时，如果{B}相对于{A}发生过旋转、平移等变换，那这一点M在两个坐标系中的坐标表示必定是不同的。这样的问题在机器人身上也十分常见，例如：机器人摄像头所捕捉到物体的坐标信息，是相对于摄像头光圈孔的，但摄像头实际上可能是被“歪七扭八”地安装在了机器人身上的任何位置。此时，如果想要得知摄像头画面中的物体相对于机器人本体（比如底盘）而言所处的位置，就必须使用一定的数学手段将物体坐标从摄像头坐标系转换到底盘坐标系。

坐标变换分为两种：旋转变换和平移变换。这两种动作任何人都会做，但关键是如何把它们用数学公式表达出来。平移变换比较简单，接下来就先介绍旋转变换。

1 旋转变换

1.1 基本旋转变换

我们知道，点M的坐标其实也可以表示矢量OM，而向量一般都是由x轴、y轴、z轴三个方向的基向量（单位向量）按某种比例组成的。比如{B}系的xyz三个轴上的单位向量就分别为：（在{B}系自身看来）

$^B\boldsymbol{i}=\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix},\; ^B\boldsymbol{j}=\begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix},\; ^B\boldsymbol{k}=\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}$

自然，向量OM（或者说点M）就是由以上这3个基向量构成，并且3个基向量各自的比例就是点M的坐标 $^B\boldsymbol{p}_M$ 。也就是说，坐标 $^B\boldsymbol{p}_M$ 描述了由O点与M点构成的位置矢量 $\overrightarrow{OM}$ 是以什么样的比例由{B}系中的基向量组成的：

$\overrightarrow{OM}={^B\boldsymbol{i}}\,{^Bx_M}+{^B\boldsymbol{j}}\,{^By_M}+{^B\boldsymbol{k}}\,{^Bz_M} =\begin{bmatrix} 1 & 0 & 0\\ 0 & 1 &0 \\ 0 &0 & 1 \end{bmatrix}{^B\boldsymbol{p}_M}$

同样的点M在{A}看来呢？先从最简单的情形开始，假设{B}和{A}一开始是重合的，而后{B}相对{A}绕z轴旋转了角度θ。这时候对于{A}系而言，由于{B}系相对于{A}绕z轴逆时针转动了一定角度θ，因此在{A}的视角下三个单位向量就变成了（可以自己画图然后作投影分解验证一下）

$^A\boldsymbol{i}=\begin{bmatrix} \cos{\theta} \\ \sin{\theta} \\ 0 \end{bmatrix},\; ^A\boldsymbol{j}=\begin{bmatrix} -\sin{\theta} \\ \cos{\theta} \\ 0 \end{bmatrix},\; ^A\boldsymbol{k}=\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}$

但是，无论从哪个坐标系来看，向量OM始终是OM，它还是由那三个名为ijk的基向量按一定的比例来组成。因此，OM仍然可以用那三个基向量来描述，只不过在{B}系中，三个基向量带左上标“B”，而在{A}系中那三个基向量变成了带有左上标“A”的形式。此时，向量OM变为

$\overrightarrow{OM}= \begin{bmatrix} \cos{\theta} & -\sin{\theta}&0\\ \sin{\theta} & \cos{\theta} &0\\ 0 &0&1\end{bmatrix} {^B\boldsymbol{p}_M}$

自然而然，OM还可以被{A}自己的三个基向量描述：

$\overrightarrow{OM}= \begin{bmatrix}1& 0&0\\ 0 & 1 &0\\ 0 &0&1\end{bmatrix} {^A\boldsymbol{p}_M}$

接下来就可以得到：

${^A\boldsymbol{p}_M}= \begin{bmatrix} \cos{\theta} & -\sin{\theta}&0\\ \sin{\theta} & \cos{\theta} &0\\ 0 &0&1\end{bmatrix} {^B\boldsymbol{p}_M}$

也就是说，向量OM（或点M）在{B}中的坐标，左乘一个矩阵，就可以变为由{A}系所描述的坐标。回想发生这样变换的大背景：{B}系相对于{A}绕z轴逆时针转动了θ。因此，左乘上的这个矩阵就被称为旋转变换矩阵，记为

$R_{(z,\theta)}=\begin{bmatrix} \cos{\theta} && -\sin{\theta}&&0\\ \sin{\theta} && \cos{\theta} &&0\\ 0 &&0&&1\end{bmatrix}$ (1)

并且很容易验证其逆变换可以用逆矩阵来表示，同时可知旋转变换矩阵是正交的（逆等于转置）。

$R_{(z,-\theta)}=\begin{bmatrix} \cos{\theta} & \sin{\theta}&0\\ -\sin{\theta} & \cos{\theta} &0\\ 0 &0&1\end{bmatrix}=R^{-1}_{(z,\theta)}=R^{\mathrm{T}}_{(z,\theta)}$ (2)

同理可继续推导绕x轴、绕y轴的情况，这里直接给出相应旋转变换矩阵的结果：

$R_{(x,\theta)}=\begin{bmatrix} 1&0&0\\ 0 &\cos{\theta} & -\sin{\theta}\\ 0 &\sin{\theta} & \cos{\theta}\end{bmatrix}=R^{-1}_{(x,-\theta)}R^{\mathrm{T}}_{(x,\theta)}$ (3)

$R_{(y,\theta)}=\begin{bmatrix} \cos{\theta} &0& \sin{\theta}\\ 0&1&0\\-\sin{\theta}& 0 & \cos{\theta}\end{bmatrix}=R^{-1}_{(y,-\theta)}=R^{\mathrm{T}}_{(y,\theta)}$ (4)

1.2 通用旋转变换

以上三种变换是极其特殊的，因为它们都是绕最特殊的三个轴旋转得来的结果。而在一般情况下，物体或坐标系的旋转可能是任意的，这就需要引入以下的通用旋转变换。

1.2.1 由转轴与转角求变换矩阵

若新的坐标系不是由绕旧坐标系x、y、z这三根特殊的转轴旋转而成，而是绕另一任意的转轴（用单位向量表示）

$\boldsymbol{f}=\begin{bmatrix} f_x & f_y & f_z \end{bmatrix}^\mathrm{T},\;\left \| \boldsymbol{f} \right \|=1$ (5)

旋转θ角得来的，那么相应的旋转变换矩阵记作 $\mathrm{Rot}\left (\boldsymbol{f},\theta \right )$ 。这里直接给出以下结论：

$\mathrm{Rot}\left (\boldsymbol{f},\theta \right ) =\begin{bmatrix} f_x f_x\mathrm{vers}{\theta}+\cos\theta & f_y f_x\mathrm{vers}{\theta}-f_z\sin\theta & f_z f_x\mathrm{vers}{\theta}+f_y\sin\theta \\ f_x f_y\mathrm{vers}{\theta}+f_z\sin\theta& f_y f_y\mathrm{vers}{\theta}+\cos{\theta} & f_z f_y\mathrm{vers}{\theta}-f_x\sin\theta \\ f_x f_z\mathrm{vers}{\theta}-f_y\sin\theta& f_y f_z\mathrm{vers}{\theta}+f_x\sin\theta & f_z f_z\mathrm{vers}{\theta}+\cos\theta\end{bmatrix}$ (6)

其中， $\mathrm{vers}\theta:=1-\cos{\theta}$ .

也就是说，只要我们知道了转轴的坐标表示和旋转的角度，就可以直接依据(6)写出相应的旋转变换矩阵。这样，新坐标系下的任意一点的坐标，只需左乘这一旋转矩阵(6)，就可以得到用旧坐标系视角下的坐标。

1.2.2 由变换矩阵求转轴与转角

反过来，如果我们知道了某一旋转变换的矩阵（此处要求变换矩阵必须是正交矩阵），同样可以求解出对应的等效转轴与旋转角度。

若已知某一旋转变换矩阵

$R_{(\boldsymbol{f},\theta)}=\begin{bmatrix} n_x & o_x & a_x\\ n_y & o_y & a_y\\ n_z & o_z & a_z \end{bmatrix}$ (7)

则相应的转角和转轴（单位向量）可由下式计算：

$\theta =\arctan{\left [\dfrac{\sqrt{(o_z-a_y)^2+(a_x-n_z)^2+(n_y-o_x)^2}}{n_x+o_y+a_z-1} \right ]}$ (8)

$\boldsymbol{f}=\begin{bmatrix} \dfrac{o_z-a_y}{2\sin{\theta}} \\ \\ \dfrac{a_x-n_z}{2\sin{\theta}} \\ \\ \dfrac{n_y-o_x}{2\sin{\theta}} \end{bmatrix}$ (9)

由于{B}系是由{A}系绕f旋转θ而来，再求{B}系中某点在{A}系中的坐标，这样的变换记为从{B}到{A}的旋转变换： $^A_B\boldsymbol{R}$ .

2 平移变换

相对于旋转变换而言，平移变换就很简单。假设{B}系的原点处于{A}系的 $^A\boldsymbol{p}_{B_0}\in\mathbb{R}^3$ 处，而某一点N在{B}系中的坐标为 $^B\boldsymbol{p}_N\in\mathbb{R}^3$ ，则点N在{A}中的坐标为：

$^A\boldsymbol{p}_N={^A\boldsymbol{p}_{B_0}}+{^B\boldsymbol{p}_N}$ , (10)

用中学知识就可以理解。

3 齐次变换

3.1 基本其次变换

齐次变换是指叠加了先旋转、后平移的变换过程，用式子表示为：

$^A\boldsymbol{p}_M={^A_B\boldsymbol{R}}{^B\boldsymbol{p}_M}+{^A\boldsymbol{p}_{B_0}}$ (11)

如果将坐标的维数进行增广，用4维的向量和矩阵来描述，虽然多出来的一个维度看起来没什么大用，也不具有实际的物理意义，但这样却可以方便地同时表示出旋转和平移：

$\left[ \begin{array} {c} {^A\boldsymbol{p}_M} \\ \hline 1 \end{array}\right ]=\underbrace{\left[ \begin{array} {c|c} {^A_B\boldsymbol{R}} &{^A\boldsymbol{p}_{B_0}}\\\hline0 & 1\end{array}\right ]}_{^A_B{\boldsymbol{T}}} \left[ \begin{array} {c} {^B\boldsymbol{p}_M} \\ \hline 1 \end{array}\right ]$ (12)

称4维的变换矩阵为齐次变换矩阵：

$^A_B\boldsymbol{T}=\left[ \begin{array}{ccc|c} n_x & o_x &a_x & p_x\\ n_y & o_x &a_x & p_x\\ n_z & o_x &a_x & p_x\\ \hline 0 & 0 &0 &1\\ \end{array}\right]$ (13)

该矩阵的各列依次构成了法线矢量 $\boldsymbol{n}$ 、方向矢量 $\boldsymbol{o}$ 、接近矢量 $\boldsymbol{a}$ 和原点矢量 $\boldsymbol{p}$ . 特别地，若4维矢量的第4行为0，可以理解为该矢量长度无限远。

齐次变换的逆变换具有如下性质，可作为一种快速求解逆矩阵的方法：

$\left ({^A_B\boldsymbol{T}} \right )^{-1}={^B_A\boldsymbol{T}}=\left[ \begin{array} {c|c} {^A_B\boldsymbol{R}}^{\mathrm{T}} &-\left ({^A_B\boldsymbol{R}}^{\mathrm{T}} \right ){^A\boldsymbol{p}_{B_0}}\\\hline0 & 1\end{array}\right ]$ (14)

前述的3种基本旋转变换如果用齐次变换的形式来表示，则分别记为：

$\mathrm{Rot}(z,\theta)=\left[ \begin{array}{ccc|c} \cos{\theta} & -\sin{\theta}&0 & 0\\ \sin{\theta} & \cos{\theta} &0&0\\ 0 &0&1&0 \\ \hline 0 & 0 & 0 & 1 \end{array} \right ]$ (15)

$\mathrm{Rot}(y,\theta)=\left[ \begin{array}{ccc|c}\cos{\theta} &0& \sin{\theta}&0\\ 0&1&0&0\\-\sin{\theta}& 0 & \cos{\theta}&0\\\hline0&0&0&1\end{array} \right ]$ (16)

$\mathrm{Rot}(x,\theta)=\left[ \begin{array}{ccc|c}1&0&0&0\\ 0&\cos{\theta} & -\sin{\theta}&0\\ 0&\sin{\theta} & \cos{\theta}&0\\ \hline 0 & 0 & 0 & 1 \end{array} \right ]$ (17)

而平移变换则记作

$\mathrm{Trans}(x,r)=\left[ \begin{array}{ccc|c} 1&0&0&r\\ 0&1&0&0 \\ 0&0&1&0 \\ \hline 0&0&0&1 \end{array} \right ]$ (18)

$\mathrm{Trans}(y,r)=\left[ \begin{array}{ccc|c} 1&0&0&0\\ 0&1&0&r \\ 0&0&1&0 \\ \hline 0&0&0&1 \end{array} \right ]$ (19)

$\mathrm{Trans}(z,r)=\left[ \begin{array}{ccc|c} 1&0&0&0\\ 0&1&0&0 \\ 0&0&1&r \\ \hline 0&0&0&1 \end{array} \right ]$ (20)

3.2 相对变换与绝对变换

当若干个变换同时发生时，最关键的是要弄清变换发生的顺序，进而确定变换矩阵之间的运算关系。依据变换发生时所参考坐标系的不同，可将坐标（齐次）变换分为相对变换与绝对变换两种。

相对变换：第一次变换发生后，第二次变换是相对于新形成的坐标系继续发生的。

例如，{A}系绕x_A轴旋转角θ，得到中间坐标系{M}，{M}系绕其自身的、同时也是新形成的z_M轴旋转角φ，得到坐标系{B}，则{B}到{A}的坐标变换矩阵为：

$^A_B\boldsymbol{T}=\textup{Rot}(x,\theta)\textup{Rot}(z,\phi)$ (21)

绝对变换：无论先后发生多少次变换，都是相对同一坐标系（称为绝对坐标系）而言的变换。

例如，{A}系绕x_A轴旋转角θ，得到中间坐标系{M}，{M}继续绕原本的z_A轴旋转角φ，得到坐标系{B}，则{B}到{A}的坐标变换矩阵为：

$^A_B\boldsymbol{T}=\textup{Rot}(z,\phi)\textup{Rot}(x,\theta)$ (22)

注意，相对变换中历次变换矩阵的运算规律为依次右乘，而绝对变换中则为依次左乘。

4 几种位姿描述方法

上述变换矩阵除了表示坐标系的变换关系，还与物体的位置和姿态（统称位姿）描述有关。接下来将分别介绍几种常用的位姿描述方法。

4.1 姿态描述方法

4.1.1 旋转矩阵描述

为某一物体建立起与之固连的空间坐标系{E}，则用1.1所述的旋转矩阵即可表示物体坐标系{E}与另一坐标系{B}的姿态关系。换言之，用{B}系的坐标来描述{E}系的三轴单位向量，就可以唯一地确定{E}的相对姿态。旋转矩阵的本质，正是旋转后所得坐标系各个基的相对坐标表示。

虽然旋转矩阵共有9个元素，但实际上只需3个参数就可唯一描述出坐标系。这是因为任意（正交的）旋转矩阵都可以写为通用旋转变换的形式，即用转轴向量 $\boldsymbol{f}$ 与转角 $\theta$ 来描述（详见1.2）。而转轴向量又是单位向量，即 $\left \|\boldsymbol{f} \right \|=\sqrt{f_x^2+f_y^2+f_z^2}=1$ ，因此只需转轴向量三个坐标中的两个即可唯一确定转轴方向。综上，只需 $\left ( f_x,f_y,\theta \right )$ 或 $\left ( f_y,f_z,\theta \right )$ 或 $\left ( f_x,f_z,\theta \right )$ 三个参数就可描述坐标系的姿态。

然而，用旋转矩阵确定坐标系的姿态总是不大方便的，因为人们往往不能一看到矢量坐标就立即想象出其具体方向。因此，又引入了另外几种更加符合人们直观感受的姿态描述法。

4.1.2 旋转序列法（欧拉角）描述

该方法通过三次绝对旋转变换来描述坐标系的姿态，分别是先绕z轴旋转 $\psi$ ，再绕y轴旋转 $\theta$ ，最后再绕z轴旋转 $\phi$ （当然，也可以用相对旋转变换来定义欧拉角，不过这样的话顺序刚好相反）。此时对应的旋转矩阵为：

$\mathrm{Euler}(\psi,\theta,\phi)=\mathrm{Rot}(z,\phi)\mathrm{Rot}(y,\theta)\mathrm{Rot}(z,\psi)$ (23)

反之，如果知道任意的以旋转矩阵表示的姿态

$R=\begin{bmatrix} n_x & o_x & a_x\\ n_y & o_y & a_y\\ n_z & o_z & a_z \end{bmatrix}$

则可反解出三个旋转角（也称欧拉角）的值：

$\begin{cases} \phi=\arctan{\left ( \dfrac{a_y}{a_x} \right )} \\ \\ \theta=\arctan{\left (\dfrac{a_x\cos{\phi}+a_y\sin{\phi}}{a_z} \right )} \\ \\ \psi=\arctan{\left (\dfrac{n_y\cos{\phi}-n_x\sin{\phi}}{o_y\cos{\phi}-o_x\sin{\phi}} \right )} \end{cases}$ (24)

4.1.3 横滚、俯仰、偏转（RPY）描述

这种姿态描述方法在飞行器方面应用较多。在建立坐标系时，通常先确定某一方向（通常为飞行器前进方向）为z轴正方向，则绕z轴旋转称为横滚(Roll)，绕y轴旋转称为俯仰（Pitch），绕x轴旋转称为偏转（Yaw）。在描述物体的姿态时，假设物体先绕z旋转，在此基础上继续绕y旋转，最后继续绕新的z旋转，可知此时为相对变换。相应转角依次记为 $(\psi,\theta,\phi)$ .由此得到的旋转矩阵为：

$\mathrm{RPY}(\phi,\theta,\psi)=\mathrm{Rot}(z,\phi)\mathrm{Rot}(y,\theta)\mathrm{Rot}(x,\psi)$ (25)

反之，如果知道任意的以旋转矩阵表示的姿态，同样可反解出RPY角的值： $\begin{cases} \phi=\arctan{\left ( \dfrac{n_y}{n_x} \right )} \\ \\ \theta=\arctan{\left (-\dfrac{n_z}{n_x\cos{\phi}+n_y\sin{\phi}} \right )} \\ \\ \psi=\arctan{\left (\dfrac{a_x\sin{\phi}-a_y\cos{\phi}}{o_y\cos{\phi}-o_x\sin{\phi}} \right )} \end{cases}$ (26)

综上，可以发现，在三维空间中，无论使用哪种姿态描方法，都可以使用3个参数唯一确定一个姿态，这正反映了空间所具有的三个旋转自由度。

4.2 位置描述方法

我们知道，平移变换（或不考虑姿态的纯位置坐标）用齐次变换矩阵表示为

$\boldsymbol{T}=\left[ \begin{array}{ccc|c} 1 & 0& 0 &p_x\\ 0 &1 & 0 & p_y\\ 0& 0& 1 &p_z\\ \hline 0 & 0 &0 &1\\ \end{array}\right]$

因此，物体在坐标系中的位置完全可以认为是由原点平移得来，也就是说用xyz三个坐标可以描述位置，同样分别与空间中三个平动自由度相对应。除此之外，还可以结合角度来描述位置，比如柱坐标描述与球坐标描述。

4.2.1 柱坐标描述

用柱坐标描述空间中某一点的参数有3个，分别表示竖直高度（柱高）、水平长度（柱半径）和高度角，如图x所示，记为：

$\mathrm{Cyl}\left ( z,\alpha,r \right )$ (27)

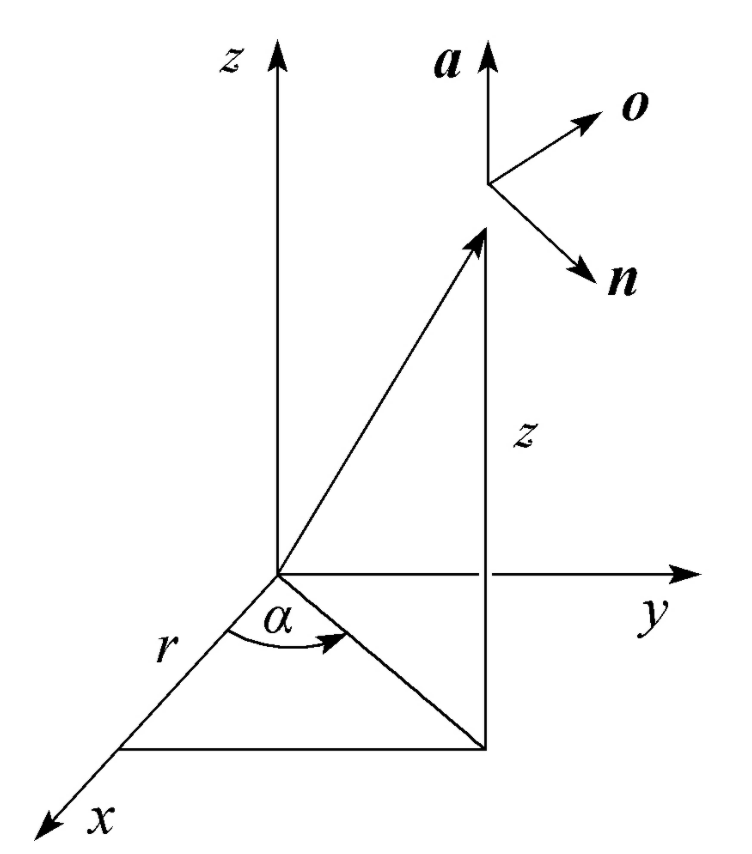
根据几何关系容易得其正解和逆解：

$\begin{cases} p_x=r\cos{\alpha}\\ \\ p_y=r\sin{\alpha}\\ \\ p_z=z \end{cases}$ , $\begin{cases} z=p_z \\ \\ \alpha=\arctan{\left ( \dfrac{p_y}{p_x} \right )} \\ \\ r=\dfrac{p_x}{\cos{\alpha}}=\dfrac{p_x}{\sin{\alpha}} \end{cases}$ (28)

4.2.2 球坐标描述

用球坐标描述空间中某一点的参数也有3个，分别表示方位角、高度角和球半径，如图y所示，记为：

$\mathrm{Sph}\left ( \alpha,\beta,r \right )$ (29)

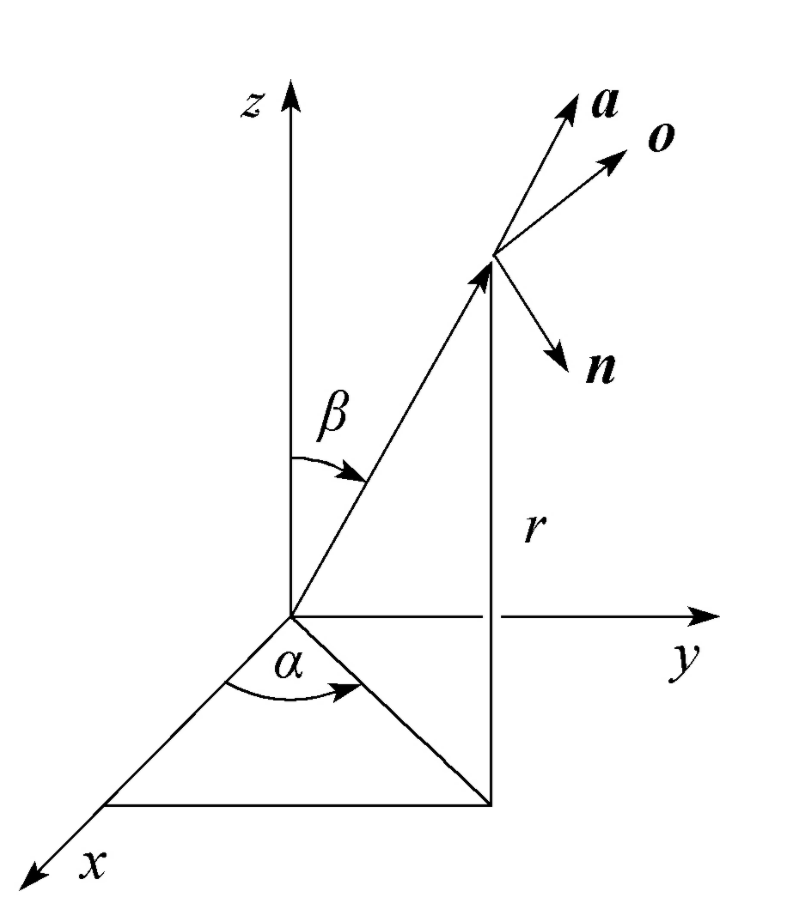
根据几何关系容易得其正解和逆解：

$\begin{cases} p_x=r\sin{\beta}\cos{\alpha} \\ \\ p_y=r\sin{\beta}\sin{\alpha} \\ \\ p_z=r\cos{\beta} \end{cases}$ , $\begin{cases} \alpha=\arctan{\left ( \dfrac{p_y}{p_x} \right )} \\ \\ \beta=\arctan{\left ( \dfrac{p_x}{p_z\cos{\alpha}} \right )} =\arctan{\left ( \dfrac{p_x\cos{\alpha}+p_y\sin{\alpha}}{p_z} \right )} \\ \\ r=\dfrac{p_z}{\cos{\beta}}=\sin{\beta}\left ( p_x \cos{\alpha}+p_y\sin{\alpha} \right )+p_z\cos{\beta} \end{cases}$ (30)

一些教材使用了后一个等号的形式，这与前一个等号的表达式是完全等价的。

至此本文内容结束。下篇将继续梳理机器人运动学、动力学和控制算法等方面的知识，敬请关注！

参考文献

[1] 蔡自兴, 谢斌编著. 机器人学[M]. 清华大学出版社, 2015.
[2] (日)白井良明编著. 机器人工程[M]. 科学出版社, 2001.
[3] 樊泽明等编著. 机器人学基础[M]. 机械工业出版社, 2022.

-- 友情链接 --

【玩转倒立摆】（一）一阶倒立摆之 - 数学模型的建立

【玩转倒立摆】（二）一阶倒立摆之 - 基于全状态反馈的极点配置方案

-- 内容预告 --

-- 更新中 --

【状态空间漫游记】系列
【状态空间漫游记】（一）卡尔曼滤波 (Kalman Filter) 算法的基本原理与代码实现
【状态空间漫游记】（二）模型参考自适应控制（MRAC）之局部参数最优化方法（MIT律）
【玩转倒立摆】系列
【玩转倒立摆】（三）一阶倒立摆之 - 基于分离原理的状态观测器方案
【玩转倒立摆】（四）一阶倒立摆之 - 最优线性二次调节器（LQR）方案
【玩转机械臂】系列
【玩转机械臂】（二）机器人DH参数模型与正、逆运动学

-- 筹备中 --