【玩转倒立摆】（一）一阶倒立摆之 - 数学模型的建立

原创已于 2025-08-22 22:31:32 修改 · 2.5k 阅读

39 ·

CC 4.0 BY-SA版权

文章标签：

#数学建模 #笔记 #课程设计 #自动化

于 2025-08-16 00:12:22 首次发布

玩转倒立摆专栏收录该内容

2 篇文章

订阅专栏

笔者注：这是【玩转倒立摆】专栏的第（一）篇文章，内容主体来源于笔者近期的学习与思考。受限于笔者的学识水平，文中必定存在诸多不足之处，望广大读者海涵。
文末将附上有前后衔接关系的相应文章链接，欢迎跳转查看。

0 写在前面：何为倒立摆？

倒立摆，顾名思义就是一座”摆“，实际上与人们所熟知的”单摆“”摆钟“别无二致，只不过自动控制领域所用到的”摆“通常还与一定的运动机构紧密相连，例如由丝杠带动的滑台/小车、由电机驱动的旋臂等。人们研究这座”摆“的目标就是要使它”倒立“起来并保持不动，甚至在受到一定干扰的情况下仍能自动恢复”倒立“的状态，而不再像平时一样下垂静止或来回晃荡。

直线倒立摆（图片来源于网络，侵删）

旋转倒立摆（图片来源于网络，侵删）

在自动控制领域的广大学者看来，玩倒立摆这种既考验控制性能（保持倒立）又考验抗扰能力（自动恢复），还涉及复杂动态（非线性建模）的活计，用来检验教科书和论文里各种各样的控制方法简直再合适不过了！于是乎，PID（比例-积分-微分）、LQR（线性二次调节器）、FC（模糊控制）等轮番上阵，倒立摆已然成为了控制理论神仙们各显神通的试炼场。与此同时，砖家叫兽老湿筒靴和广大卷王们纷纷表示"就这？“，似乎还远远不过瘾，于是便接连着弄出来了二阶倒立摆、三阶倒立摆……不过，对于低年级的入门自控小白而言，能比较全面、完整地掌握一阶倒立摆就已善莫大焉。私以为，即使是简单的模型和算法，只要能够自己亲手动手推推公式、写写代码、跑跑仿真，其对自己核心能力和知识素养的提升也远远大于成天只会copy复杂算法的开源程序和做一个资深“调参大师”的。这也是为何笔者愿意几乎（你总不能指望我从高中物理开始讲起吧）从零开始梳理倒立摆的有关知识、并将相应的MATLAB仿真源码设置为付费的主要原因。

好了，废话不多说，请广大读者尤其是刚入门的小白们准备好大脑和演草纸，开始见证你是如何操练倒立摆的十八般武艺的吧！

1 倒立摆的物理方程

以直线倒立摆为例，整个运动系统的模型实际上可以抽象为一根杆+一辆车，两者固接在一起，但杆可以无摩擦地自由转动，如图1所示。其中“杆”只是一个抽象的示意，实际上杆的末端可能还连有“摆锤”，杆本身的形状也未必规则。

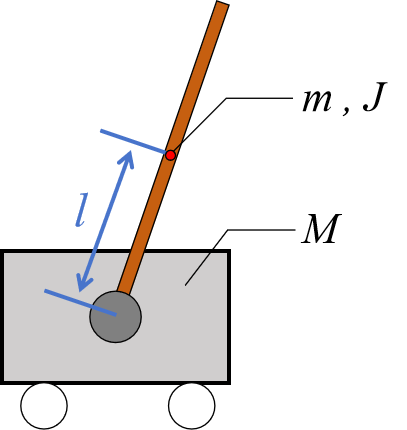
图1 倒立摆基本模型

1.1 基本参数与符号

倒立摆系统的物理参数会决定系统的动态情况。将杆和车的质量分别记为和，同时杆的重心到连接处的长度记作。由于杆绕连接点转动，故而还存在相应的转动惯量，记作。

考虑到广大读者所掌握的专业知识不尽相同，接下来将以具备高中物理+少许大学物理水平就能掌握的经典牛顿力学方法开展运动分析。此外还有基于理论力学如拉格朗日方程的分析方法，本文不再赘述，感兴趣的读者可参阅如下链接：

1024Robot-倒立摆建模推导https://mp.weixin.qq.com/s/2xOBDK9hAPYY6-5WDgwt-A

在进行运动学分析时，以向右为正方向，将小车的位移（以右端界限参考）记为，将杆的水平位移（以重心为参考）记为；以向上为正方向，将杆的竖直位移记作。为使今后的倒立摆控制问题成为点镇定问题（将所有状态量调节到0），本文选取摆杆与竖直向上射线之间的夹角作为摆角，并以顺时针为正方向。注意，夹角0°位置的选取十分重要，0°位置的不同将影响最终推出的运动方程。

在进行动力学分析时，向右为正方向，记人为施加的外界作用力为。为简便分析，将小车所受的所有摩擦均抽象为一个与速度成正比的“阻尼力”，阻尼系数为；也就是说，系统受到的总摩擦用来刻画。此外，将小车推动杆、杆反作用于小车的两个相互作用力分别分解到水平和竖直方向上，并分别记为和，如图2所示。

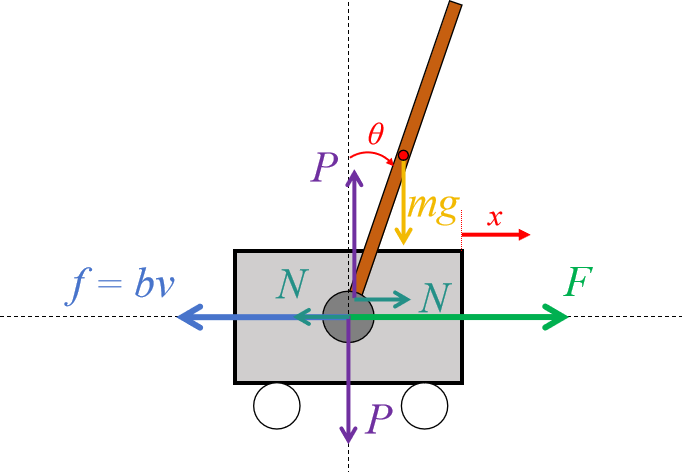
图2 倒立摆受力分析示意图

1.2 物理方程的推导

首先，对小车的受力情况进行分析。由于小车只在水平方向运动，竖直方向上存在可以抵消一切其他的竖直受力的支持力。因此，依据牛顿第二定律可以很容易地写出水平方向上小车动力学方程：

. (1)

其次，分析摆杆的受力情况。在小车的推动下，在瞬时内，可认为杆绕其质心发生转动，同时摆杆整体还叠加了平移运动。先考虑转动，取力和分别在杆垂直的方向上的分量、，其作用点到转动轴心的距离恰好为，则可得出力矩与转动角加速度的关系（注意顺时针转动的方向为正）为

. (2)

再分析杆的平动，可知叠加发生的平动包含水平、竖直两个方向，其动力学关系为

. (3)

由于杆与车是固连的，几何规则限制了杆的平动位移与转动角度之间的定量关系，即小车的质心永远被限制在以为半径的圆上。此外，由于杆的转动是相对于小车参考系而言的，因此从大地参考系来看，其实际平动位移还应加上小车的位移。综上有

. (4)

将(4)代入(3)消去和，再将结果依次代入(1)(2)消去中间作用力和，就可以得到仅包含小车位移及其导数、摆杆摆角及其导数的动态物理方程。需要注意的是，(4)代入(3)时需要对时间求导，此时应牢记并正确使用复合函数的求导法则，许多人正是在求导这一步上计算出错，导致推出的模型与正确模型相去甚远。(4)式求二阶导后的结果应为：

. (5)

受篇幅所限，这里直接给出最终的倒立摆动态（微分）物理方程：

. (6)

2 状态空间模型的建立

关于状态空间（State Space）的基本知识，请读者自行参阅相关的自动控制原理教科书。对于(6)式所示的物理方程，很容易可以想到用位移、速度、角度、角速度来作为状态空间中的状态变量（State Variables），即

由于状态空间表达式遵循“导数在左、状态在右”的原则，因此需要通过代换消元将(6)式中的和单独分离出来放在等式左边，得到如下所示的非线性状态空间表达式：

, (7)

其中

. (8)

方程(7)精确地描述了一阶倒立摆系统的运动情况，只要初始条件确定、外力（控制）作用已知，则借助数值计算方法（如改进欧拉法、龙格-库塔法等）就可较精确地描绘出系统运行过程的细节。然而，在实际设计控制律时，(7)式很少会被直接使用，而通常采用其线性化后的“简化版本“，这也是下一节将要重点阐述的内容。

3 系统模型的线性化（重点）

在(7)中，大量的三角函数使得整个系统变得十分复杂，直接对这样的非线性系统进行控制是比较困难的。因此，人们通常只在一定范围内（不超过±30°）对倒立摆施加平衡控制作用。在此范围内，三角函数可以被较好地线性近似，使得系统的复杂度大大降低，进而让设计者能够使用人们所熟知的PID、LQR等线性系统方法进行控制。

3.1 线性化的条件与方法

在进行系统的线性化之前，首先需要明确系统的工作点（Operating Point），并在工作点附近进行线性化。这个过程就类似于在二维曲线上某点处作切线、在三维曲面某点上作切平面。显然，如果系统运行的状态偏离事先选取的”工作点“越远，那么线性模型所描述的精度也就越差。因此，模型线性化的首要条件就是系统必须运行在所选取的工作点附近。至于”附近“究竟是多大的范围，就需要具体问题具体分析了。对于本文所建立的倒立摆系统而言，由于控制方式是进行点镇定，因此选取为工作点（若采用了其他的建模方法，则工作点的选取可能会不同）。此时范围内的线性效果通常都是可以接受的；而如果追求更高的精度，则一般取为宜。

在确定好系统工作点和可行范围之后，就可以对非线性的系统模型进行线性化操作。最通用的方法是将非线性函数在工作点附近进行Taylor展开，并略去二阶及以上的项：

其中是Jacobian矩阵：

不过，对于本文中的倒立摆系统(7)而言，线性化操作实际上并不需要这么麻烦。将时存在的近似关系：

. (9)

代入前面推导出的物理方程(6)中，就可以得到线性化后的物理方程

. (10)

此时的系统就是一个线性时不变（LTI）系统，可以进一步转换成传递函数、状态空间等形式，从而直接使用Routh-Hurwitz判据、根轨迹法、Nyquist判据、Bode图、Luenberger观测器、全状态反馈极点配置等传统方法加以分析和控制。

3.2 倒立摆的线性状态空间模型

传递函数模型将在后续关于PID及其改进型控制器的文章中详细讨论，本文先给出(10)式的线性状态空间表达式：

, (11)

此外，若系统具有位移传感器和角度编码器，则系统输出可表示为

, (12)

式(11)和(12)共同构成了用状态空间表示的完整LTI系统，这将是后续使用多种控制方法来“玩转”倒立摆的基础。

参考文献

[1] 胡寿松, 自动控制原理（第五版）[M].科学出版社,2007.
[2] 黄孝平, 基于遗传神经网络的倒立摆控制研究[M].重庆大学出版社,2014.
[3] Richard C. Dorf , Robert H. Bishop. Modern Control Systems (Eleventh Edition) [M]. 电子工业出版社, 2009.

-- 友情链接 --

下一篇：【玩转倒立摆】（二）一阶倒立摆之 - 基于全状态反馈的极点配置方案

-- 内容预告 --

-- 更新中 --

【玩转倒立摆】系列
【玩转倒立摆】（三）一阶倒立摆之 - 状态观测器与嵌入式实现
【状态空间漫游记】系列
【状态空间漫游记】（一）卡尔曼滤波 (Kalman Filter) 算法的基本原理与代码实现

-- 筹备中 --

【玩转机械臂】系列
【玩转机械臂】（一）坐标变换与DH参数基础
【玩转机械臂】（二）机械臂的正、逆运动学
【玩转倒立摆】系列
【玩转倒立摆】（四）一阶倒立摆之 - 模型预测控制方案
【玩转倒立摆】（五）一阶倒立摆之 - 模糊控制方案
【玩转倒立摆】（六）一阶倒立摆之 - 神经网络控制方案
【状态空间漫游记】系列
【状态空间漫游记】（二）初探自适应：模型参考&自校正控制导论
【玩转无人机】系列