目录
上篇文章介绍了针对传递函数的变增益法、和变参数法两种自适应控制方案,本文将针对状态空间继续给出两种类型自适应控制方法:增益反馈型(KF法)、状态反馈型(GF法)。
对于状态空间而言,模型参考自适应控制实际上就是让实际模型跟随某一确定的理想模型,即模型跟随控制。在介绍自适应方法之前,首先给出参数已知条件下的模型跟随控制方法。
1 状态空间的直接模型跟随控制
1.1 理想模型跟随
假设期望的理想模型,即参考模型为
其参数为已知,我们的任务是通过设计合适的控制律u,使实际模型
与已知的参考模型保持一致。为此,可以将控制律设计为具有输入前馈与状态反馈的形式:
(1)
从而使得实际的闭环系统变为
对比已知模型,求解期望的增益矩阵:
(2)
其中控制矩阵B取伪逆(左伪逆)
能够使得控制矩阵B在不为方阵时也满足
特别地,如果B本身可逆,就有。换言之,只要按(2)式确定增益矩阵,就可以让实际系统完全跟随参考系统。
1.2 模型跟随的埃尔茨贝格条件
然而,并非所有系统都能被完全地跟随,因为左伪逆右乘于原矩阵时,并不能保证结果为单位矩阵,即
这就会造成当我们把由(2)确定的控制律代入实际系统时,模型跟随的等式左右两边不一定成立。而模型跟随等式成立(能够实现理想跟随),当且仅当以下条件满足:
(3)
该式也称模型跟随控制的埃尔茨贝格(Erzberger)条件。在实际应用中,首先应当验证所设计的参考模型与实际模型是否满足上述条件,若不满足,就不能使用本文所讨论的自适应控制策略。
2 增益反馈型自适应模型跟随控制
由前一节可知,当实际系统与参考系统满足Erzberger条件时,能够实现理想的模型跟随。然而,实际的模型通常未知,或存在参数误差,因而理想中的目标增益矩阵是无法直接求解的。为此,引入以下自适应方法,使实际系统在运行过程中逐渐修正并最终跟随上参考模型。
2.1 方法推导
首先介绍增益反馈型的自适应模型跟随控制,一般将反馈矩阵记作F、增益前馈矩阵记作K,故又称KF法。首先定义如下的误差矩阵:
以及广义误差
由此可得广义误差的状态方程为
我们知道,如果实际模型的参数均已知,则由(2)可得理想的目标矩阵为F*与K*,即满足
因此有
(4)
其中的维度关系为:
选取待定Lyapunov函数为
(5)
其中,进而求得导数
(6)
其中正定矩阵Q应满足Lyapunov方程
对于矩阵的迹(trace),有如下性质:。并且由于
对称,因此有
同理可得
则(6)式可进一步写为
(7)
由于,均为标量,而对于标量有
成立。 此外,由于矩阵的迹具有性质
,因此可知
这样,所形成的p×p的矩阵就可以与(7)式中的最后两项的维度相匹配,从而得到
要使系统渐进稳定,可令最后两项均为0,即
由于误差增益矩阵的定义是,因此前馈增益和反馈增益的自适应律为
(8)
注意,项带有负号是因为控制律(1)式选取的是状态负反馈的形式;若选取状态正反馈,则符号正好相反。
2.2 仿真示例
仿真MATLAB源码请到文末链接获取下载。
我们以无刷直流电机的二阶近似模型为例。考虑以下系统:
其中
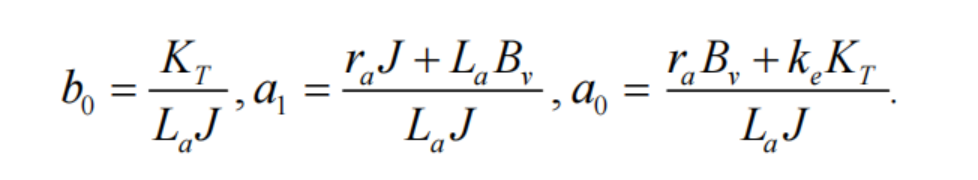
系统参数由实际电机决定,本例中取参考模型参数(即理想参数/目标参数)为

而实际参数则是未知的,与理想值存在一定偏差,具体取值请参见文末源码。
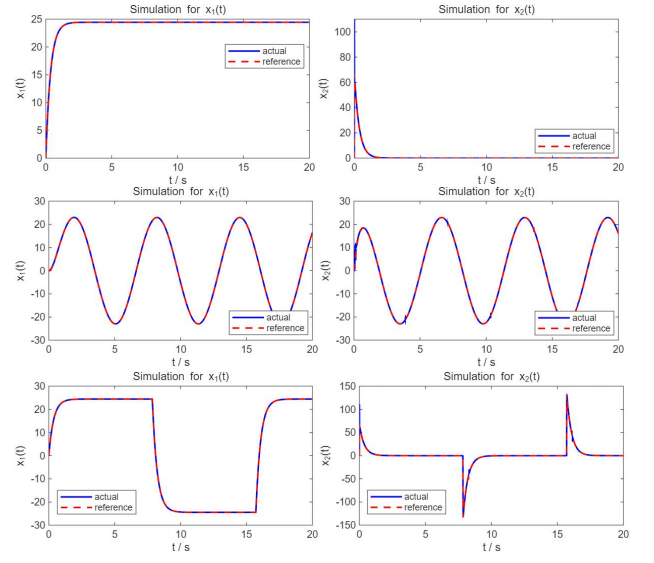
首先进行无MRAC的运行对比,其中红色虚线表示参考模型的参考输出,即理想/目标的输出曲线;蓝色实线为同一输入作用下的实际系统输出曲线。可见二者之间存在一定的差异,这在反映了实际中建模不准、模型失配的问题。
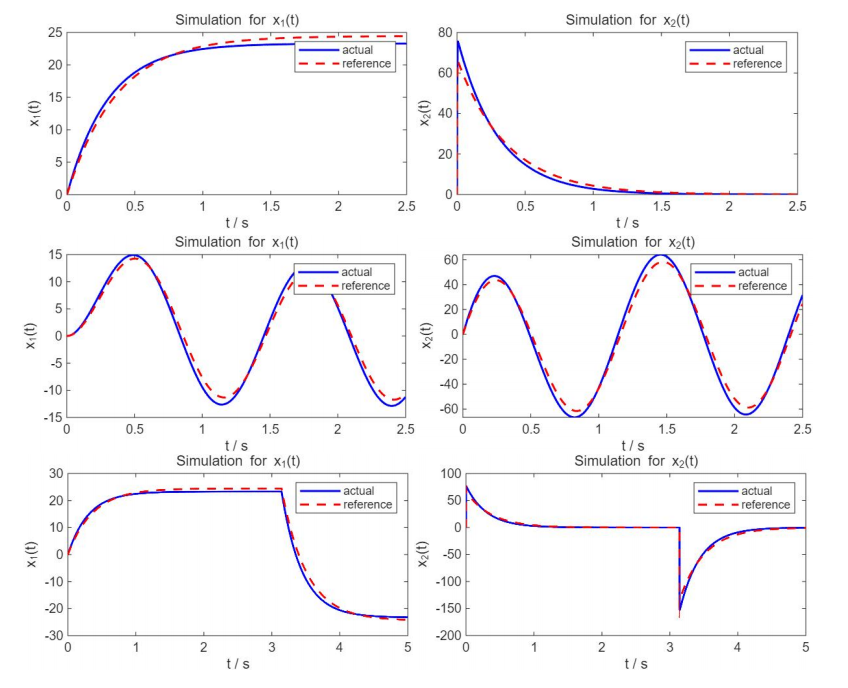
随后加入本节所述的MARC方法,可见实际输出完全跟踪上了参考模型的输出,模型失配问题得以校正。
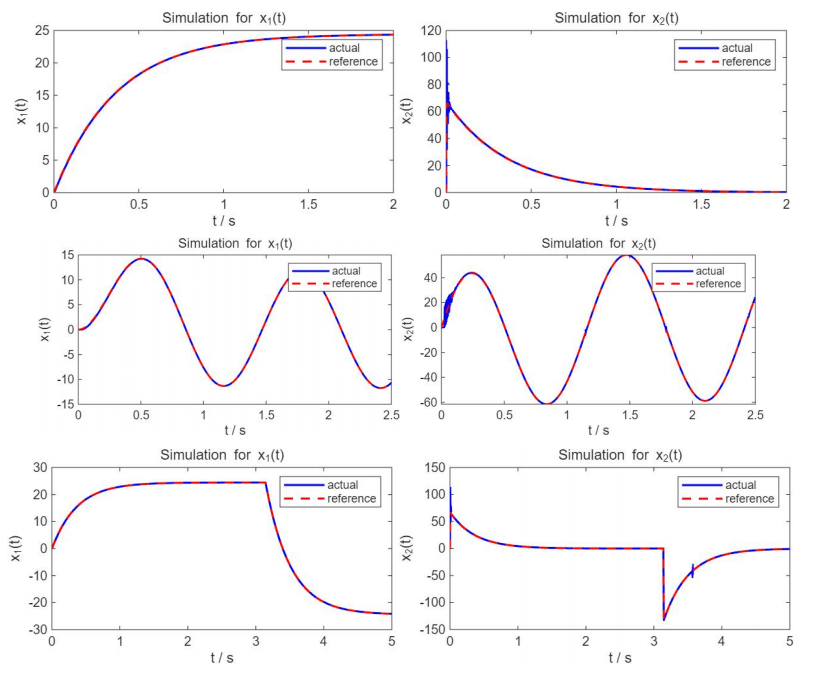
以上展示的是参数未知但恒定的情况,接下来考虑模型参数时变影响下的控制性能。假设系统参数会随时间发生缓慢的变化,造成结果如下图所示,可见实际输出与参考输出存在较大的差异。
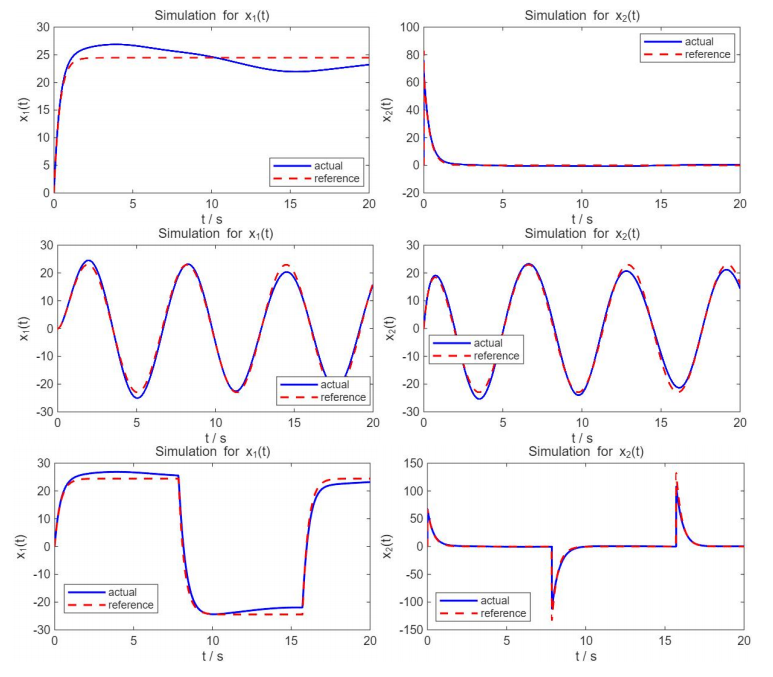
引入MRAC后,可以看到系统输出在参数时变条件下仍能跟随参考输出。
3 状态反馈型自适应模型跟随控制
前一节所介绍的KF法是最常用的MRAC方法之一。然而,该方法也存在一个最严重的不足:自适应律(8)使用了实际模型的控制矩阵,而这一般而言是未知的。针对此,一般有两种解决办法:1)用参考模型的控制矩阵近似代替;2)用系统辨识的方法获取控制矩阵。不过这两种方法总是不大方便的,我们总是希望自适应律中完全不含有未知的量。而本节所提供的方法就可以解决这一点。
3.1 方法推导
KF法需要用到未知控制矩阵的的本质原因是,状态反馈所得的控制输入加到了实际模型的输入上,也就是说状态反馈的信号必须直接经过控制矩阵,才能影响到被控系统。因此,如果能够避免状态反馈信号直接经过控制矩阵,例如先与前馈信号进行综合,之后再进入被控系统,就能较好地解决该问题。
基于此,设计如下与(1)式不同的控制律,可简称为GF法:
(9)
则闭环系统方程变为
同样地,在参数已知的情况下,我们希望能够直接找到F*和G*,时闭环系统等同参考系统:
(10)
继而可推出类似于KF法的等式成立条件:
(11)
式(11)称为GF型的埃尔茨贝格(Erzberger)条件。
需要注意的是,在本方法中,应当设计为可逆的,则由(10)可知
如果用来表示目标G的逆与实际G的逆之间的偏差,即
就可以得到一个容易被忽视但在后续推导过程中很有用的式子:
(12)
此外,类似KF法,定义增益误差矩阵和广义误差:
由此可得关于广义误差的状态方程:
其中是我们不愿看到的,因为它是未知量,而这时就可以使用(12)式巧妙地消去
:
因此广义误差的状态方程变为
(13)
我们希望广义误差和参数误差
均收敛,为此构建如下的待定Lyapunov函数:
(14)
与KF法类似,可得Lyapunov函数的导数为
令后两项为0,则有
(15)
接下来需要将关于误差的自适应律变换回关于增益矩阵本身的自适应律。考虑的定义,容易得到结论
;需要使用到一点技巧的是如何将
变换回
:
由于,则
,即
;考虑到参数误差的定义
,求导有
,因而可得
(16)
综上,最终的自适应律为
(17)
3.2 仿真示例
仿真Simulink文件请到文末链接获取下载。
本例的实际系统为:
参考系统为:
假设状态量全部已知,即输出矩阵为单位矩阵。
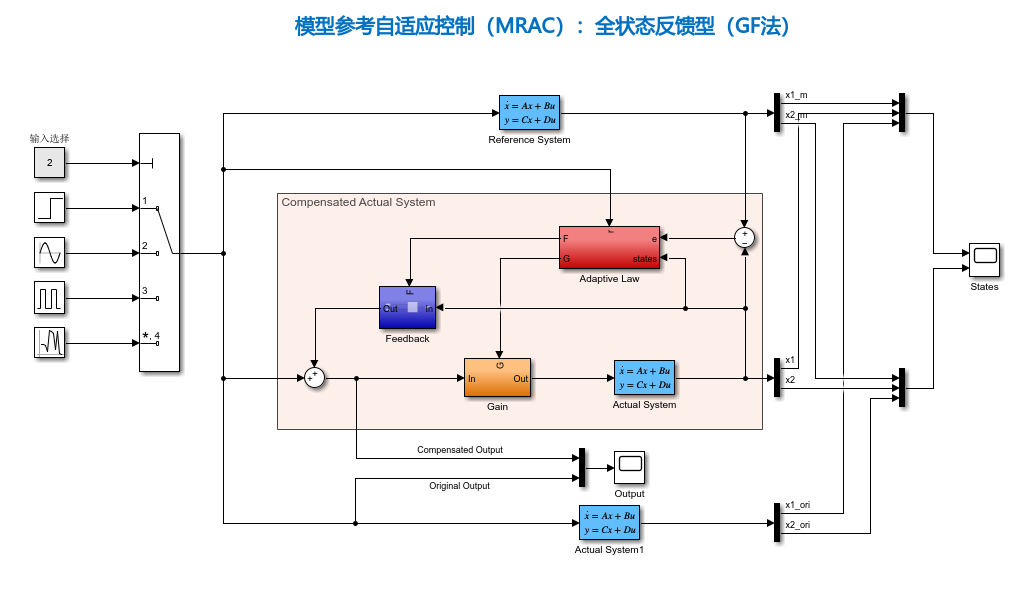
仿真结果如下图所示,其中红色虚线为参考模型的状态量,蓝色实线为实际系统的状态量,绿色实线为未加入自适应律的实际系统状态量。
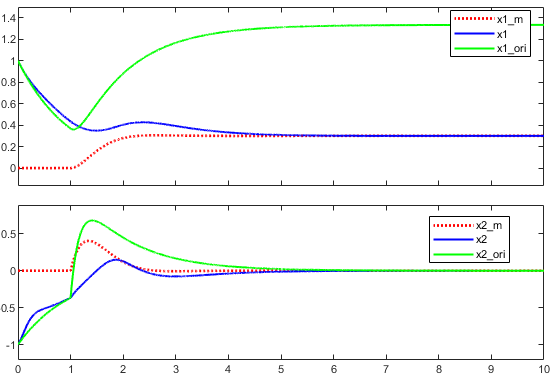
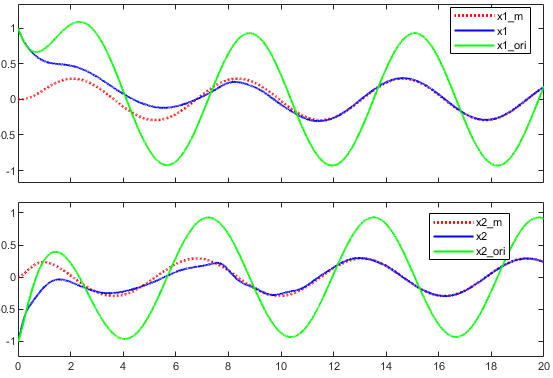
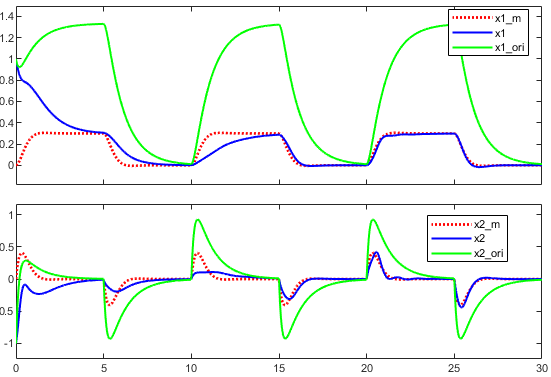
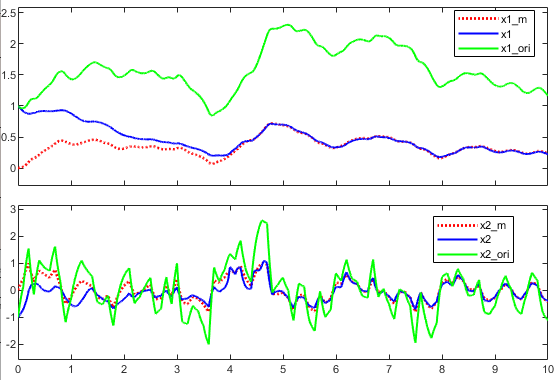
至此,模型参考自适应控制的内容已基本结束。接下来的几篇文章将继续讨论基于最小二乘辨识的自校正控制。
参考文献
[1] 柴天佑, 岳恒. 自适应控制[M]. 北京: 清华大学出版社, 2016.
[2] 董宁. 自适应控制[M]. 北京理工大学出版社, 2009.
下载链接
【免费】模型参考自适应控制(MRAC):增益反馈型方法的MATLAB仿真程序资源-优快云下载![]() https://download.youkuaiyun.com/download/ych0872/92418424?spm=1001.2014.3001.5503【免费】模型参考自适应控制(MRAC):全状态反馈型方法的Simulink仿真程序资源-优快云下载
https://download.youkuaiyun.com/download/ych0872/92418424?spm=1001.2014.3001.5503【免费】模型参考自适应控制(MRAC):全状态反馈型方法的Simulink仿真程序资源-优快云下载![]() https://download.youkuaiyun.com/download/ych0872/92419932?spm=1001.2014.3001.5503
https://download.youkuaiyun.com/download/ych0872/92419932?spm=1001.2014.3001.5503
友情链接
【状态空间漫游记】(二)模型参考自适应控制(MRAC):局部参数最优化方法(MIT律)_mrac设计原理以及稳定性分析与自适应律推导-优快云博客
【状态空间漫游记】(三)模型参考自适应控制(MRAC):基于传递函数的自适应控制(变增益法、变参数法)-优快云博客





















 1642
1642

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








