目录
在前一篇文章中,我们已经了解了最简单的自适应控制规律——MIT律。然而MIT律适用性较差,需满足除增益外的系统完全一致的假设,且难以保证闭环控制系统的稳定性。本文将基于Lyapunov稳定性理论等方法推导适用性更强的自适应控制方法。
众所周知,传递函数和状态空间是最常用的两种系统模型,且线性条件下二者可以相互等价转换。本文先讨论基于传递函数的自适应控制方法,分为变增益型和变参数型两种;有关状态空间的方法将在下一篇文章中再进一步讨论。
1 基础理论
基于传递函数的自适应控制方法所需的数学基础理论包括Lyapunov稳定性理论、正实函数理论、KYP引理等。它们的详细介绍及证明过程请参见有关专业资料,本文仅从应用的角度简要介绍其与自适应控制理论有关的部分。以下数学理论较为枯燥,若无兴趣的读者可直接阅读第2节。
1.1 Lyapunov稳定性理论
Lyapunov方法是最常用的稳定性分析工具之一,常见的现代控制理论教材均对该理论作了详细的介绍,以下仅简要回顾:
定理1.1 (线性系统渐进稳定)自由响应的线性系统渐进稳定的充分必要条件是:
,
. (1)
式(1)称为Lyapunov方程,相应的Lyapunov函数为:
.
1.2 正实函数理论
正实函数是针对复函数定义的概念,本文使用的是其加强后的定义“严格正实函数”。
定义1.1 (严格正实函数)复变量的函数
满足以下条件:
1)
2) 在右半复平面上无极点(解析)
3)
则称为严格正实(Strictly Positive Real, S.P.R)函数。
若某一传递函数是严格正实函数,即
则其拥有以下性质:
性质1.1 (严格正实传递函数的性质)
1) 的Nyquist曲线必在右半复平面(RHP),因而闭环系统必然稳定;
2) 相对阶数。
此外,对于严格正实函数有以下的正实函数引理:
引理1.1 (Kalman-Yakubovich-Popov引理)对于LTI系统
及其传递函数
,
若,则等价于满足Lyapunov方程(1)并且
, (2)
2 变增益法MRAC
2.1 基本结构
变增益型的基本结构与MIT律所使用的结构一致,同样需要假设实际模型除增益外的其余部分与参考模型完全一致。区别在于,MIT律采用基于梯度信息的局部优化方法,而本方法采用Luyapunov方法来保证了自适应控制律的稳定性。
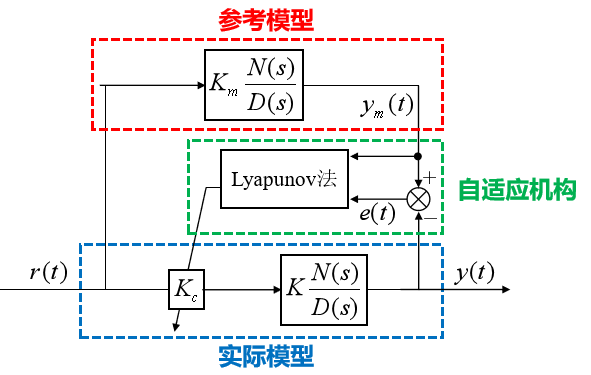
该方法的主要结构依旧包括参考模型、实际模型、可调部分及自适应机构,所用信号为广义误差和参考输出等。
2.2 方法推导
2.1.1 能观标准型
首先假设除增益外的传递函数为
,
则可得输出的广义误差:
.
若定义
(3)
则关于广义误差的微分方程为
.
按以下方式选取状态变量和状态输出
可得状态方程为
(4)
输出方程为
(5)
其中系数由以下线性方程组解得:
(6)
具体推导参见文献[3]。由(4)(5)构成的状态空间称为能观标准型(Observable Canonical Form)。
在大多数情况下,传递函数分子的阶次小于分母的阶次,此时只需令相应的系数为0即可。
2.2.2 构造Lyapunov函数
与MIT法一样,自适应控制的方法依旧是通过实时地调节,使得系统的实际输出跟随参考输出。不过,本文的要求不再仅仅局限于最优化误差指标,而是直接了当地确保广义误差渐进收敛,即关于广义误差的状态空间渐进稳定:
.
然而对于上述能观标准型
可知其稳定性不仅由系统矩阵决定,还与控制矩阵
、输入信号
以及增益误差
有关。因此,选取一个待定的李雅普诺夫函数(Candidate Lyapunov Function):
(7)
其中,且通常为对称矩阵。显然
计算其关于时间的导数:
.
由于需要保证定理1.1中;此外由
知
因此上述待定Lyapunov函数可进一步写作
. (8)
2.2.3 导出自适应律
根据Lyapunov稳定性定理,要保证系统稳定,必须有。基于此,如果令(8)中除了关于状态向量的二次型之外的所有项都为0,即
(9)
则可得
,
满足Lyapunov稳定性定理,系统渐进稳定。因此,(9)式是一种可行的自适应律设计方式。
由于时
,要使(9)式成立,则必须有
即
故可得:
(10)
实践中,获知通常是不容易的。因此借助正实函数的KYP引理,考虑
且相对阶不大于1的情况,假设相应传递函数满足S.P.R.,则式(2)成立:
由此(10)式可进一步化为
其中,同时记
,则可得最终的自适应律:
(11)
与MIT法相比,自适应律(11)使用的是系统输入,而非参考输出
,是一种前馈补偿的思想。
注意:若系统的相对阶大于1,则必不满足S.P.R.条件,此时只能使用(10)式作为自适应律。对于已知的传递函数,可先验证其是否S.P.R,若是,则不必使用广义误差的各阶导数,只用即可;若否,则只能使用状态向量
,同时还要计算能观标准型的控制矩阵
和解Lyapunov方程得
.
2.3 仿真示例
由于变增益法与MIT法仅有较小的差别,其仿真结果也相近,因此不再赘述相关的仿真过程,可参考前一篇文章中的MIT法仿真结果。
【状态空间漫游记】(二)模型参考自适应控制(MRAC):局部参数最优化方法(MIT律)-优快云博客![]() https://blog.youkuaiyun.com/ych0872/article/details/152175663?spm=1001.2014.3001.5501【免费】模型参考自适应控制(MRAC):局部参数最优化方法(MIT律)Simulink仿真模型资源-优快云下载
https://blog.youkuaiyun.com/ych0872/article/details/152175663?spm=1001.2014.3001.5501【免费】模型参考自适应控制(MRAC):局部参数最优化方法(MIT律)Simulink仿真模型资源-优快云下载![]() https://download.youkuaiyun.com/download/ych0872/92354278?spm=1001.2014.3001.5503
https://download.youkuaiyun.com/download/ych0872/92354278?spm=1001.2014.3001.5503
3 变参数法MRAC
无论是MIT法还是本文先前讨论的变增益法,都存在一个根本性缺陷——它们都假设参考模型与实际模型仅有增益上的差异,而这一假设在实际中往往过于严苛。一方面,实际系统的结构参数(除增益外的其他参数)通常是未知的;另一方面,即使已知结构参数,这两种方法也只能通过调整增益来改善系统性能。换言之,基于增益自适应的控制方法仅能使系统闭环极点沿根轨迹移动,无法实现极点的任意配置,具有很大的局限性。
因此,更加合理的做法是,不仅对系统增益进行自适应调节,同时还通过一定的方法对实际系统的结构参数也进行自适应调节,使其完全地能够跟踪任意参考模型的运动状态。
3.1 基本结构
首先假设参考模型的传递函数为
, (12)
而实际系统的传递函数是
, (13)
其中系统结构参数经过前馈、反馈等环节的补偿后均直接可调。
3.2 方法推导
3.2.1 能控标准型
接下来的目标就是如何设计的调节规律,使得它们能尽可能地与参考模型参数
保持一致。为此,定义如下的参数误差及参数误差向量:
(14)
, (15)
进而可得微分方程:
两式相减,可得关于广义误差的微分方程:
等式两边同时减去
,再同时加上
,可得
(16)
注意!为防止正负号出现错误,我们特别强调:参数误差应定义为实际量(可调量)减去参考量,而广义误差定义为参考量减去实际量。
根据(16)式建立状态空间,选取状态向量为
则状态方程为
, (17)
其中
可知该状态空间为一能控标准型(Controllable Canonical Form)。
3.2.2 构造Lyapunov函数
由(17)可知,该系统的稳定性不仅与参考模型参数有关,还与时变的参数误差
有关。因此,选取待定Lyapunov函数为:
(18)
其中,且通常为对称矩阵。显然有
继续计算时间导数:
由各矩阵的相应维度可知:
因此可将Lyapunov函数的导数写作
(19)
并同时满足Lyapunov方程(1)。
3.2.3 导出自适应律
假设系数矩阵
,
计算可得
假设系数矩阵
计算可得
由此可进一步将(19)式展开为
在上式中,由于尚不确定,
的负定性不能保证,因此可以令
从而使得,系统渐进稳定。考虑到(14)的定义,由此导出自适应律为:
(20)
3.3 仿真示例
在本例中,假设实际系统模型和参考模型分别为
要使G(s)参数可调,可以考虑引入内环反馈和增益前馈,如下图所示:
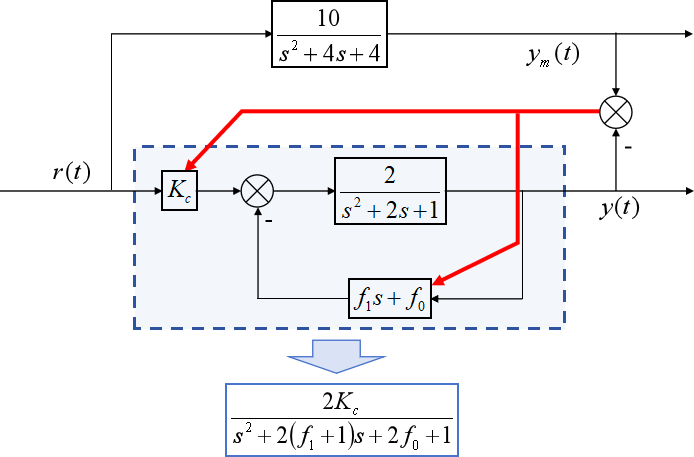
由此将实际系统校正为结构参数任意可调的系统:
令,则与先前所推结论保持一致的形式。
由传递函数建立(17)式中的系统矩阵,并设定相应的正定矩阵:
解Lyapunov方程(1)可得
直接应用式(20)的结论,得到参数自适应律:
继续反推即可写出关于的自适应调节规律。
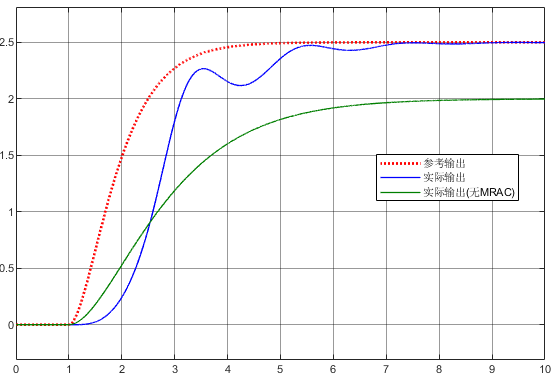
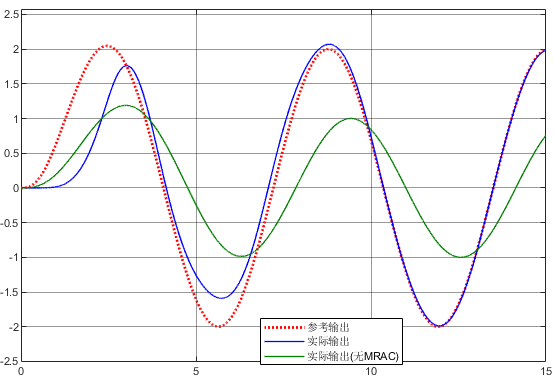
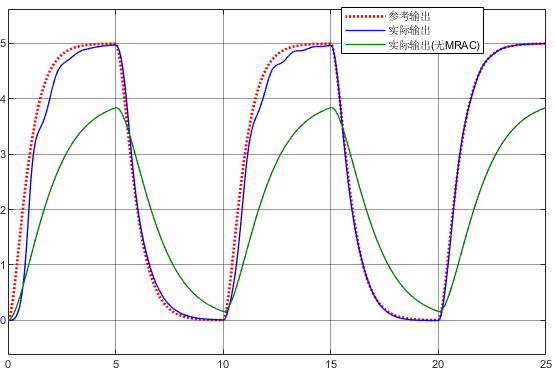
将以上结果使用Simulink进行仿真,取,结果如下图所示。源文件请移步文末链接获取。
参考文献
[1] 董宁. 自适应控制[M]. 北京理工大学出版社, 2009.
[2] 柴天佑, 岳恒. 自适应控制[M]. 北京: 清华大学出版社, 2016.
[3] 胡寿松, 姜斌等. 自动控制原理(第八版)[M].科学出版社, 2023: 452-453.
下载链接
注:slx文件基于Matlab2024a版本,使用较低版本Matlab可能无法打开,可在S“imulink-建模-环境-Simulink预设项-模型文件”中去除勾选“不要加载用更新版本的Simulink创建的模型”。
友情链接
【状态空间漫游记】(二)模型参考自适应控制(MRAC):局部参数最优化方法(MIT律)-优快云博客
【玩转机械臂】(一)机器人学的数学基础:坐标变换与位姿描述_机械臂坐标变换-优快云博客
【玩转倒立摆】(一)一阶倒立摆之 - 数学模型的建立-优快云博客





















 5364
5364

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








