第十讲：主成分分析（Principal components analysis）

前面我们讲了因子分析（factor analysis），其中在某个 $k$ 维度子空间对 $x\in R^n$ 进行近似建模，$k$ 远小于 $n$，即 $k\ll n$。具体来说，我们设想每个点 $x^{(i)}$ 用如下方法创建：首先在 $k$ 维度仿射空间（affine space） $\Lambda z+\mu ;z\in R^k$ 中生成某个 $z^{(i)}$ ，然后增加 $\Psi$-协方差噪音（covariance noise）。因子分析（factor analysis）是基于一个概率模型（probabilistic model），然后参数估计（parameter estimation）使用了迭代期望最大化算法（iterative EM algorithm）。

在本章讲义中，我们要学习一种新的方法，主成分分析（Principal Components Analysis，缩写为 PCA），这个方法也是用来对数据近似（approximately）所处的子空间（subspace）进行判别（identify）。然而，主成分分析算法（PCA）会更加直接，只需要进行一种特征向量（eigenvector）计算（在 Matlab 里面可以通过 eig 函数轻松实现），并且不需要再去使用期望最大化（EM）算法。

假如我们有一个数据集 { x(i);i=1,...,m}\{x^{(i)}; i = 1, . . ., m\}{ x(i);i=1,...,m}，其中包括了 $m$ 种不同汽车的属性，例如最大速度（maximum speed），转弯半径（turn radius）等等。设其中每个 $i$ 都有 $x^{(i)}\in R^n，(n\ll m)$。但对于两个不同的属性，例如 $x_i$ 和 $x_j$，对应着以英里每小时（mph）为单位的最高速度和以公里每小时（kph）为单位的最高速度。因此这两个属性应该基本是线性相关（linearly dependent）的，只在对 mph 和 kph 进行四舍五入时候会有引入一些微小差异。所以，这个数据实际上应该是近似处于一个 $n-1$ 维度的子空间中的。我们如何自动检测和删除掉这一冗余（redundancy）呢？

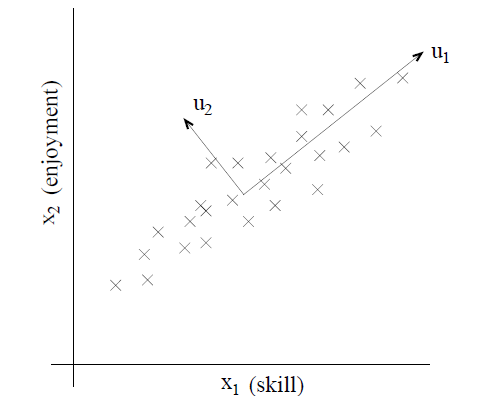
举一个不那么麻烦的例子，设想有一个数据集，其中包含的是对一个无线电遥控直升机（radio-controlled helicopters）飞行员协会进行调查得到的数据，其中的 $x_1^{(i)}$ 指代的是飞行员 $i$ 的飞行技能的度量，而 $x_2^{(i)}$ 指代的是该飞行员对飞行的喜爱程度。无线电遥控直升机是很难操作的，只有那些非常投入，并且特别热爱飞行的学生，才能成为好的飞行员。所以，上面这两个属性 $x_1$ 和 $x_2$ 之间的相关性是非常强的。所以我们可以认为在数据中沿着对角线方向（也就是下图中的 $u_1$ 方向）表征了一个人对飞行投入程度的内在“源动力（karma）”，只有少量的噪音脱离这个对角线方向。如下图所示，我们怎么来自动去计算出 $u_1$ 的方向呢？

图 1 飞行员协会调查数据

我们接下来很快就要讲到主成分分析算法（PCA algorithm）了。但在运行 PCA 之前，我们首先要进行一些预处理（pre-process），正则化（normalize）数据的均值（mean）和方差（variance），如下所示：

1. Let μ=1m∑i=1mx(i)\mu=\frac1m\sum_{i=1}^mx^{(i)}