在强化学习中,马尔科夫决策过程(Markov decision process, MDP)是对完全可观测的环境进行描述的,也就是说观测到的状态内容完整地决定了决策的需要的特征。几乎所有的强化学习问题都可以转化为MDP。本讲是理解强化学习问题的理论基础。
下面将从以下四个部分展开介绍:
- 马尔科夫过程 Markov Process
- 马尔科夫奖励过程 Markov Reward Process
- 马尔可夫决策过程 Markov Decision Process
- MDP延伸 Extensions to MDPs
1. 马尔科夫过程 Markov Process
- 马尔科夫性 Markov Property
某一状态信息包含了所有相关的历史,只要当前状态可知,所有的历史信息都不再需要,当前状态就可以决定未来,则认为该状态具有马尔科夫性。
可以用下面的状态转移概率公式来描述马尔科夫性:
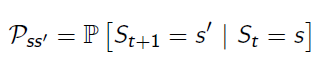
下面状态转移矩阵定义了所有状态的转移概率:

式中n为状态数量,矩阵中每一行元素之和为1。
- 马尔科夫过程 Markov Property
马尔科夫过程 又叫马尔科夫链(Markov Chain),它是一个无记忆的随机过程,可以用一个元组<S,P>表示,其中S是有限数量的状态集,P是状态转移概率矩阵。
- 示例——学生马尔科夫链
本讲多次使用了学生马尔科夫链这个例子来讲解相关概念和计算。
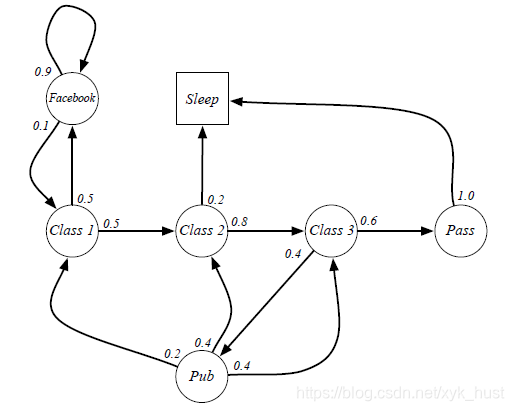
图中,圆圈表示学生所处的状态,方格Sleep是一个终止状态,或者可以描述成自循环的状态,也就是Sleep状态的下一个状态100%的几率还是自己。箭头表示状态之间的转移,箭头上的数字表示当前转移的概率。
举例说明:当学生处在第一节课(Class1)时,他/她有50%的概率会参加第2节课(Class2);同时他/她也有50%的概率没有认真听课,进入到浏览facebook这个状态中。在浏览facebook这个状态时,他/她有90%的概率在下一时刻继续浏览,也有10%的概率返回到课堂内容上来。当学生进入到第二节课(Class2)时,会有80%的概率继续参加第三节课(Class3),也有20%的概率觉得课程较难而退出(Sleep)。当学生处于第三节课这个状态时,他有60%的概率通过考试,继而100%的退出该课程,也有40%的可能性需要到去图书馆之类寻找参考文献,此后根据其对课堂内容的理解程度,又分别有20%、40%、40%的概率返回值第一、二、三节课重新继续学习。一个可能的学生马尔科夫链从状态Class1开始,最终结束于Sleep,其间的过程根据状态转化图可以有很多种可能性,这些都称为Sample Episodes。以下四个Episodes都是可能的:
- C1 - C2 - C3 - Pass - Sleep
- C1 - FB - FB - C1 - C2 - Sleep
- C1 - C2 - C3 - Pub - C2 - C3 - Pass - Sleep
- C1 - FB - FB - C1 - C2 - C3 - Pub - C1 - FB - FB - FB - C1 - C2 - C3 - Pub - C2 - Sleep
该学生马尔科夫过程的状态转移矩阵如下图所示:
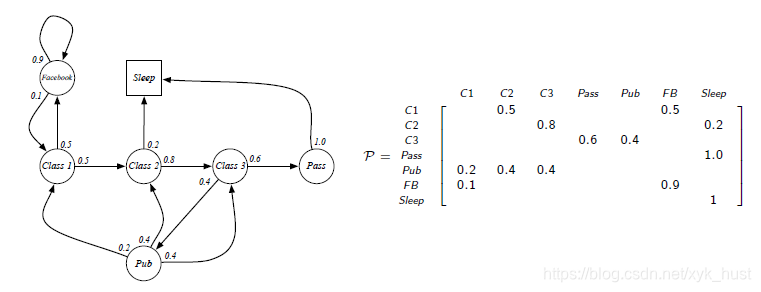
2. 马尔科夫奖励过程 Markov Reward Process
马尔科夫奖励过程在马尔科夫过程的基础上增加了奖励R和衰减系数γ:<S,P,R,γ>。R是一个奖励函数。S状态下的奖励是某一时刻(t)处在状态s下在下一个时刻(t+1)能获得的奖励期望:
![R_{s} = E[R_{t+1} | S_{t} = s ]](https://i-blog.csdnimg.cn/blog_migrate/becfc431fcd417ea3738b159a80dbd9d.png)
很多听众纠结为什么奖励是(t+1)时刻的。照此理解起来相当于离开这个状态才能获得奖励而不是进入这个状态即获得奖励。David指出这仅是一个约定,为了在描述RL问题中涉及到的观测O、行为A和奖励R时比较方便。他同时指出如果把奖励改为  而不是
而不是  ,只要规定好,本质上意义是相同的,在表述上可以把奖励描述为“当进入某个状态会获得相应的奖励”。
,只要规定好,本质上意义是相同的,在表述上可以把奖励描述为“当进入某个状态会获得相应的奖励”。
衰减系数 Discount Factor: γ∈ [0, 1],它的引入有很多理由,其中优达学城的“机器学习-强化学习”课程对其进行了非常有趣的数学解释。David也列举了不少原因来解释为什么引入衰减系数,其中有数学表达的方便,避免陷入无限循环,远期利益具有一定的不确定性,符合人类对于眼前利益的追求,符合金融学上获得的利益能够产生新的利益因而更有价值等等。
下图是一个“马尔科夫奖励过程”图示的例子,在“马尔科夫过程”基础上增加了针对每一个状态的奖励,由于不涉及衰减系数相关的计算,这张图并没有特殊交代衰减系数值的大小。
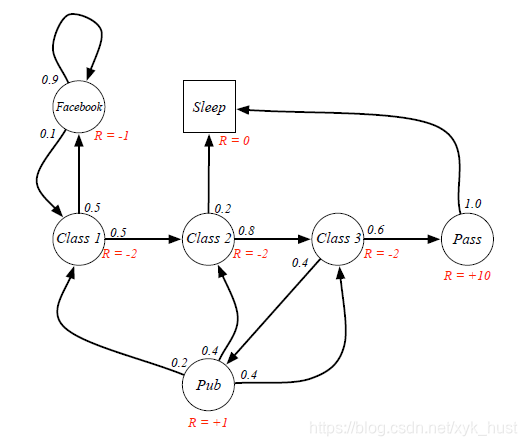
2.1 回报 Return
定义:回报  为在一个马尔科夫奖励链上从t时刻开始往后所有的奖励的有衰减的总和。也有翻译成“收益"。公式如下:
为在一个马尔科夫奖励链上从t时刻开始往后所有的奖励的有衰减的总和。也有翻译成“收益"。公式如下:
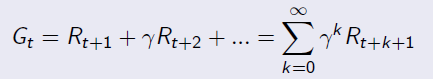
其中衰减系数体现了未来的奖励在当前时刻的价值比例,在k+1时刻获得的奖励R在t时刻的体现出的价值是  ,γ接近0,则表明趋向于“近视”性评估;γ接近1则表明偏重考虑远期的利益。
,γ接近0,则表明趋向于“近视”性评估;γ接近1则表明偏重考虑远期的利益。
2.2 价值函数 Value Function
价值函数给出了某一状态或某一行为的长期价值。
定义:一个马尔科夫奖励过程中某一状态的价值函数为从该状态开始的马尔可夫链收获的期望:








 本文深入探讨了强化学习的基础——马尔科夫决策过程(MDP),包括马尔科夫过程、马尔科夫奖励过程、马尔科夫决策过程以及MDP的延伸。通过学生马尔科夫链的例子,详细解释了状态转移概率、奖励函数、衰减系数γ、价值函数和最优策略等相关概念,并展示了如何计算不同状态的价值。
本文深入探讨了强化学习的基础——马尔科夫决策过程(MDP),包括马尔科夫过程、马尔科夫奖励过程、马尔科夫决策过程以及MDP的延伸。通过学生马尔科夫链的例子,详细解释了状态转移概率、奖励函数、衰减系数γ、价值函数和最优策略等相关概念,并展示了如何计算不同状态的价值。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 1621
1621

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








