数据结构——二叉排序树的删除操作（递归法）

karwen2020

已于 2022-08-29 20:36:57 修改

阅读量1.3k

点赞数 1

分类专栏： C语言文章标签：数据结构 c++ c语言

于 2022-08-29 18:41:44 首次发布

本文链接：https://blog.youkuaiyun.com/xinzhi1992/article/details/126590076

版权

C语言专栏收录该内容

32 篇文章

订阅专栏

1、被删除的节点是叶子节点
将双亲节点中相应的指针域的值改为空
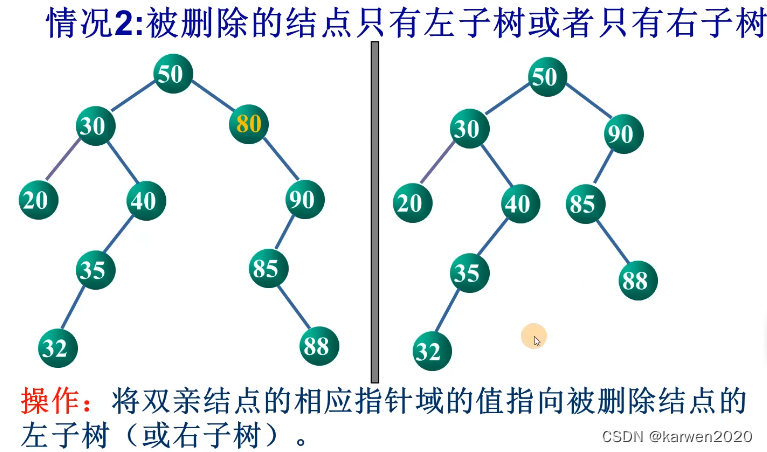
在这里插入图片描述

2、被删除的节点只有左子树或右子树
将要删除的节点的双亲节点相应指针域的值指向被删除节点的左子树或者右子树
在这里插入图片描述

3、被删除节点既有左子树又有右子树
将左子树中的最大值或者右子树中的最小值代替该节点
在这里插入图片描述
代码如下：

typedef struct TreeNode{
    int data;
    struct TreeNode *left,*right;
}TreeNode,*BiTNode;//定义了TreeNode结构体和结构体指针BiTNode
int Delete(BiTNode *rootPtr){//传入的参数为二级结构体指针
    BiTNode root,node;
    if((*rootPtr)->right == NULL){//右子树为空，则重接左子树
        root = *rootPtr;
        *rootPtr = (*rootPtr)->left;
        free(root);
    }else if((*rootPtr)->left == NULL){//左子树为空，则重接右子树
        root = *rootPtr;
        *rootPtr = (*rootPtr)->right;
        free(root);
    }else{  //左右子树均不为空
        root = *rootPtr;
        node = (*rootPtr)->left;
        while(node->right){//找到要删除节点左子树的最右节点，即左子树的最大值
            root = node;
            node = node->right;
        }
        (*rootPtr)->data = node->data;
        if(root != *rootPtr){
            root->right = node->left;//重接root的右子树
        }else{
            root->left = node->left;//重接root的左子树
        }
        free(node);
    }
    return TRUE;
}
int DeleteTreeNode(BiTNode *root, int data){//第一个参数root为二级指针
    if(*root == NULL){//空树直接返回
        return FALSE;
    }else{  //寻找数据为data的节点二叉树节点
        if(data == (*root)->data){
            return Delete(root);//找到就执行删除节点的操作
        }else if(data < (*root)->data){
            return DeleteTreeNode(&(*root)->left, data);//要找的数据小，往左子树找
        }else{
            return DeleteTreeNode(&(*root)->right, data);//要找的数据大，往右子树找
        }
    }
}

或者直接使用二级结构体指针

typedef struct TreeNode{
    int data;
    struct TreeNode *left,*right;
}TreeNode;
int Delete(TreeNode** rootPtr){//我们想修改TreeNode*类型的值，因此需传入二级指针TreeNode**才能修改
    TreeNode * root,*node;
    if((*rootPtr)->left == NULL){
        root = *rootPtr;
        *rootPtr = (*rootPtr)->left;
        free(root);
    }else if((*rootPtr)->right == NULL){
        root = *rootPtr;
        *rootPtr = (*rootPtr)->left;
        free(root);
    } else{
        root = *rootPtr;
        node = (*rootPtr)->left;
        while(node->right != NULL){
            root = node;
            node = node->right;
        }
        (*rootPtr)->data = node->data;
        if(*rootPtr != root){//判断while循环是否执行
            root->right = node->left;
        }else{
            root->left = node->left;
        }
        free(node);
    }
    return TRUE;
}
int DeleteTreeNode(BiTNode *root, int data){//第一个参数root为二级指针
    if(*root == NULL){//空树直接返回
        return FALSE;
    }else{  //寻找数据为data的节点二叉树节点
        if(data == (*root)->data){
            return Delete(root);//找到就执行删除节点的操作
        }else if(data < (*root)->data){
            return DeleteTreeNode(&(*root)->left, data);//要找的数据小，往左子树找
        }else{
            return DeleteTreeNode(&(*root)->right, data);//要找的数据大，往右子树找
        }
    }
}

为什么在执行完while循环后需要判断（*rootPtr ）是否等于 root？主要目的是为了判断while循环是否执行，例如，当删除节点为12时，则需要执行else语句。
在这里插入图片描述

完整代码如下：

#include <stdio.h>
#include <stdlib.h>
#define TRUE 1
#define FALSE 0
typedef struct TreeNode{
    int data;
    struct TreeNode *left,*right;
}TreeNode,*BiTNode;
TreeNode* InsertNode(TreeNode* root,int data){//排序二叉树中插入元素
    if(!root){
        root = (TreeNode*)malloc(sizeof(TreeNode));
        root->data = data;
        root->right = NULL;
        root->left = NULL;
        return root;
    }else{
        if(root->data > data){
            root->left = InsertNode(root->left,data);
        }else if(root->data < data){
            root->right = InsertNode(root->right,data);
        }else if(root->data == data){
            return root;
        }
    }
    return root;
}
void InOrderTree(TreeNode* root){//中序遍历二叉树
    if(root == NULL){
        return;
    }
    InOrderTree(root->left);
    printf("%d->",root->data);
    InOrderTree(root->right);
}
int Delete(BiTNode *rootPtr){
    BiTNode root,node;
    if((*rootPtr)->right == NULL){//右子树为空，则重接左子树
        root = *rootPtr;
        *rootPtr = (*rootPtr)->left;
        free(root);
    }else if((*rootPtr)->left == NULL){//左子树为空，则重接右子树
        root = *rootPtr;
        *rootPtr = (*rootPtr)->right;
        free(root);
    }else{  //左右子树均不为空
        root = *rootPtr;
        node = (*rootPtr)->left;
        while(node->right){//找到要删除节点左子树的最右节点，即左子树的最大值
            root = node;
            node = node->right;
        }
        (*rootPtr)->data = node->data;
        if(root != *rootPtr){
            root->right = node->left;//重接root的右子树
        }else{
            root->left = node->left;//重接root的左子树
        }
        free(node);
    }
    return TRUE;
}
int DeleteTreeNode(BiTNode *root, int data){//第一个参数root为二级指针
    if(*root == NULL){//空树直接返回
        return FALSE;
    }else{  //寻找数据为data的节点二叉树节点
        if(data == (*root)->data){
            return Delete(root);//找到就执行删除节点的操作
        }else if(data < (*root)->data){
            return DeleteTreeNode(&(*root)->left, data);//要找的数据小，往左子树找
        }else{
            return DeleteTreeNode(&(*root)->right, data);//要找的数据大，往右子树找
        }
    }
}
int main() {
    int data[11] = {38,12,56,6,34,40,98,3,13,78,17};
    TreeNode* root = NULL;
    for(int i = 0; i < (sizeof(data)/sizeof (data[0]));i++){
        printf("第%d次插入的元素为：%d\n",i+1,data[i]);
        root =InsertNode(root,data[i]);
    }
    printf("\n");
    InOrderTree(root);
    printf("END\n");
    DeleteTreeNode(&root,12);
    InOrderTree(root);
    printf("END\n");
    DeleteTreeNode(&root,34);
    InOrderTree(root);
    printf("END\n");
    DeleteTreeNode(&root,40);
    InOrderTree(root);
    printf("END\n");
    DeleteTreeNode(&root,98);
    InOrderTree(root);
    printf("END\n");
    DeleteTreeNode(&root,78);
    InOrderTree(root);
    printf("END\n");
     DeleteTreeNode(&root,3);
    InOrderTree(root);
    printf("END\n");
     DeleteTreeNode(&root,6);
    InOrderTree(root);
    printf("END\n");
     DeleteTreeNode(&root,13);
    InOrderTree(root);
    printf("END\n");
     DeleteTreeNode(&root,17);
    InOrderTree(root);
    printf("END\n");
     DeleteTreeNode(&root,56);
    InOrderTree(root);
    printf("END\n");
    DeleteTreeNode(&root,38);
    InOrderTree(root);
    printf("END\n");


    return 0;
}

程序运行结果为：

第1次插入的元素为：38
第2次插入的元素为：12
第3次插入的元素为：56
第4次插入的元素为：6
第5次插入的元素为：34
第6次插入的元素为：40
第7次插入的元素为：98
第8次插入的元素为：3
第9次插入的元素为：13
第10次插入的元素为：78
第11次插入的元素为：17

3->6->12->13->17->34->38->40->56->78->98->END
3->6->13->17->34->38->40->56->78->98->END
3->6->13->17->38->40->56->78->98->END
3->6->13->17->38->56->78->98->END
3->6->13->17->38->56->78->END
3->6->13->17->38->56->END
6->13->17->38->56->END
13->17->38->56->END
17->38->56->END
38->56->END
38->END
END