二叉树之删除节点

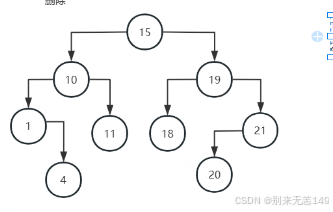
Ⅰ情况分类：

1：删除叶子节点

Ⅱ删除叶子节点

1找到要删除的节点target

2找到要删除节点的父节点

3考虑有没有父节点

4如果没有父节点那么target是根节点

5如果有父节点讨论目标结点与父节点的关系：是左孩子还是右孩子

左孩子：parent,left=null

右孩子：parent.right=null

Ⅲ删除节点具有两颗子树

用左子树的最大值或者右子树的最小值代替将要删除的节点

Ⅳ删除具有单颗子树的节点（看导航栏比较清楚）

1首先检查有没有父节点

2如果有父节点在检查目标结点间有左子树还是右子树

3左子树： parent.left=target.left

4右子树 parent.right=target.right

5没有父节点在检查有左子树还是右子树

6左子树：root.left=taget.left

7右子树：root.right=taget.right

代码就放下面了如果对您有帮助的话帮忙点个关注吧

package tree;

import java.util.LinkedList;
import java.util.Queue;

public class Binarytree {
	
	node root=null;
	//添加
	public void insert(int num) {
		node node=new node(num);
		if (root==null) {
			root=node;
			return ;
		}
		
		node index=root;
		while(true) {
			if (index.value > num) {
				if(index.left==null) {
					index.left=node;
					return ;
				}else {
					index=index.left;
				}
			}else {
				if (index.right==null) {
					index.right=node;
					return ;
				}else {
					index=index.right;
				}
			}
		}
		
	}
	//层次遍历
	public void levelorder() {
		Queue<node>queue=new LinkedList<node>();
		if(root!=null) {
			queue.add(root);
		}
		node index=null;
		while(!queue.isEmpty()) {
			index=queue.poll();
			System.out.print(index.value+ " ");
			if(index.left!=null) {
				queue.add(index.left);
			}
			if(index.right!=null) {
				queue.add(index.right);
			}
		}
	}
	
	//先序遍历
	
	public void beforeorder(node node) {
		if (node==null) {
			return ;
		}
		System.out.print(node.value+" ");
		beforeorder(node.left);
		beforeorder(node.right);
	}	
	
	
	//中序遍历
	
		public void inorder(node node) {
			if (node==null) {
				return ;
			}
			inorder(node.left);
			System.out.print(node.value+" ");
			inorder(node.right);
		}
		
		//后序遍历
		
		public void afterorder(node node) {
			if (node==null) {
				return ;
			}
			afterorder(node.left);
			afterorder(node.right);
			System.out.print(node.value+" ");
		}
		
		//查找
		public node search(int num) {
			node index=root;
			while(index!=null&&index.value!=num) {
				if(index.value>num) {
					index=index.left;
				}else {
					index=index.right;
				}
			}
			return index;
		}
		
		//查找目标节点的父节点
		public node searchparnet(int num) {
			node index=root;
			while(index!=null) {
				if ((index.left!=null&&index.left.value==num)||(index.right!=null&&index.right.value==num  )) {
					return index;
				}else if(index.value>num) {
					index=index.left;
				}else {
					index=index.right;
				}
			}
			return null;
		}
		
		//找一棵树的最小值
		public int min (node treenode) {
			node index=treenode;
			while(index.left!=null) {
				index=index.left;
			}
			return index.value;
		}
		
		
		public void delete(int num) {
			if (root==null) {
				System.out.println("空树");
					return ;
			}
			node target=search(num);
			if(target==null) {
				System.out.println("没有这个节点");
				return ;
			}
			
			
			node parent=searchparnet(num);
			//目标节点没有子节点
			if(target.left==null&&target.right==null) {
				//删除叶子节点
				//没有父节点
				if (parent==null) {
					root=null;
					return ;
				}
				//有父节点
				if (parent.left!=null&&parent.left.value==num) {
					parent.left=null;
				}else {
					parent.right=null;
				}
				
			//删除有两颗子树的节点	
			}else if(target.left!=null&&target.right!=null){
				int minvalue=min(target.right);
				delete(minvalue);
				target.value=minvalue;
				
			//删除单个子树的节点	
			}else {
				//有父节点
				if(parent==null) {
					if(target.left!=null) {
						root=root.left;
					}else {
						root=root.right;
					}
				}
				//没有父节点
				else {
					//目标节点有左孩子
					if(target.left!=null) {
						parent.left=target.left;
					}else {
						parent.right=target.right;
					}
						
				}
			}
			
		}
		
}

package tree;

public class node {
	int value;
	node left;
	node right;
	public node(int val) {
		value=val;
	}
	@Override
	public String toString() {
		return "node [value=" + value + ", left=" + left + ", right=" + right + "]";
	}
	
}

package tree;

public class test {
	public static void main(String []args) {
//		node node1=new node(15);
//		node node2=new node(10);
//		node node3=new node(1);
//		node node4=new node(11);
//		node node5=new node(20);
//		node node6=new node(21);
//		node node7=new node(18);
//		node1.left=node2;
//		node2.right=node5;
//		node2.left=node3;
//		node2.right=node4;
//		node5.left=node7;
//		node5.right=node6;
////		System.out.println(node1);
		
		Binarytree tree=new Binarytree();
		tree.insert(15);
		tree.insert(10);
		tree.insert(1);
		tree.insert(11);
		tree.insert(20);
		tree.insert(21);
		tree.insert(18);
		
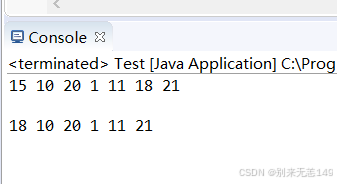
		tree.levelorder();
		System.out.println("\n");
		tree.delete(15);
		tree.levelorder();
		
	}
}