洛谷 P3266 [JLOI2015] 骗我呢

最新推荐文章于 2025-12-02 15:32:05 发布

原创最新推荐文章于 2025-12-02 15:32:05 发布 · 378 阅读

5 ·

CC 4.0 BY-SA版权

文章标签：

#算法

原题链接

不是你骗我呢，就这道题，连暴力都没打，~~崩溃了，呜呜呜~~

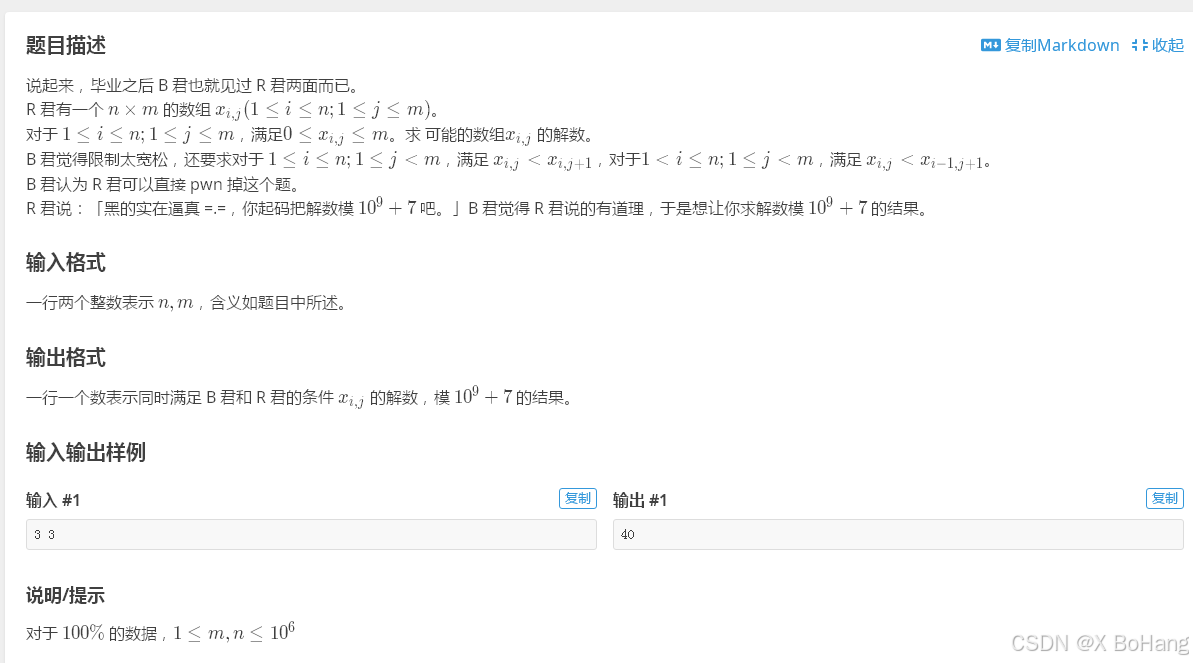
题目本质：数学+dp

题目思路：

考虑 dp。观察到每行只会有一个数字不会出现，所以设计状态 $f_{i,j}$ 为第 i 行只有 j 这个数字没出现。显然状态转移方程为 $f_{i,j}=\sum_{k=0}^{j+1}f_{i-1,k}$ 。

上界为 $j+1$ 的原因是当 $k>j+1$ 时第 i 行的 j+1 所对的位置不满足 $x_{i,j}<x_{i-1,j+1}$ 。

观察上式可以发现 $f_{i,j}$ 能由 $f_{i,j-1}$ 推来，所以有 $f_{i,j}=f_{i,j-1}+f_{i-1,j+1}$ 。

这样我们得到了 $O(nm)$ 的 dp 了。

有结论点 $(x,y)$ 关于直线 $y=x+b$ 的对称点为 $(y-b,x+b)$ ，套进去就行。

#include <bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define mk make_pair
#define ll long long
#define space putchar(' ')
#define enter putchar('\n')
using namespace std;

inline int read() {
	int x = 0, f = 1;
	char c = getchar();
	while (c < '0' || c > '9') f = c == '-' ? -1 : f, c = getchar();
	while (c >= '0' && c <= '9') x = (x<<3)+(x<<1)+(c^48), c = getchar();
	return x*f;
}

inline void write(int x) {
	if (x < 0) x = -x, putchar('-');
	if (x > 9) write(x/10);
	putchar('0'+x%10);
}

const int N = 3e6+5, mod = 1e9+7;
int n, m, k, ans, fac[N], ifac[N];

int qpow(int x, int y) {
	int res = 1;
	for (; y; y >>= 1, x = 1ll*x*x%mod) if (y&1) res = 1ll*res*x%mod;
	return res;
}

int c(int x, int y) {
	if (x < 0 || y < 0 || x < y) return 0;
	return 1ll*fac[x]*ifac[y]%mod*ifac[x-y]%mod;
}

void init(int n) {
	fac[0] = 1;
	for (int i = 1; i <= n; ++i) fac[i] = 1ll*fac[i-1]*i%mod;
	ifac[n] = qpow(fac[n], mod-2);
	for (int i = n-1; ~i; --i) ifac[i] = 1ll*ifac[i+1]*(i+1)%mod;
}

void pls(int &x, int y) { x = (x+y)%mod; }

void sub(int &x, int y) { x = (x-y+mod)%mod; }

void flip1(int &x, int &y) { swap(x, y); --x, ++y; }

void flip2(int &x, int &y) { swap(x, y); x += m+2, y -= m+2; }

int main() {
	init(N-5);
	n = read(), m = read();
	int x = n+m+1, y = n;
	ans = c(x+y, x);
	while (x >= 0 && y >= 0) {
		flip1(x, y), sub(ans, c(x+y, x));
		flip2(x, y), pls(ans, c(x+y, x));
	}
	x = n+m+1, y = n;
	while (x >= 0 && y >= 0) {
		flip2(x, y), sub(ans, c(x+y, x));
		flip1(x, y), pls(ans, c(x+y, x));
	}
	write(ans);
	return 0;
}