洛谷 P1364 医院设置

题目描述

设有一棵二叉树，如图：

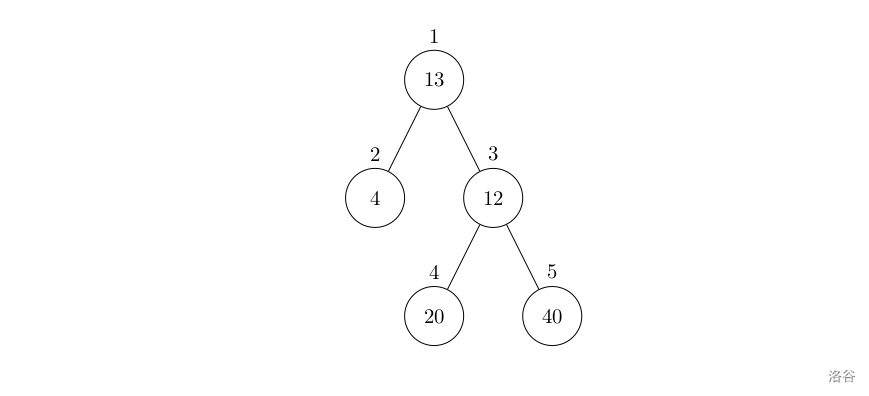
其中，圈中的数字表示结点中居民的人口。圈边上数字表示结点编号，现在要求在某个结点上建立一个医院，使所有居民所走的路程之和为最小，同时约定，相邻接点之间的距离为 11。如上图中，若医院建在 11 处，则距离和 =4+12+2\times20+2\times40=136=4+12+2×20+2×40=136；若医院建在 33 处，则距离和 =4\times2+13+20+40=81=4×2+13+20+40=81。

输入格式

第一行一个整数 nn，表示树的结点数。

接下来的 nn 行每行描述了一个结点的状况，包含三个整数 w, u, vw,u,v，其中 ww 为居民人口数，uu 为左链接（为 00 表示无链接），vv 为右链接（为 00 表示无链接）。

输出格式

一个整数，表示最小距离和。

输入输出样例

输入 #1复制

5						
13 2 3
4 0 0
12 4 5
20 0 0
40 0 0

输出 #1复制

81

说明/提示

数据规模与约定

#include<bits/stdc++.h>
using namespace std;
const int N=102;
int vis[N];
int fa[N],lchild[N],rchild[N],peo[N];
int cal(int pos,int dis){
	if(vis[pos]	||	!pos){
		return 0;
	}
	vis[pos]=1;
	int sum=0;
	sum+=peo[pos]*dis;
	sum+=cal(lchild[pos],dis+1);
	sum+=cal(rchild[pos],dis+1);
	sum+=cal(fa[pos],dis+1);
	return sum;
}
int main(){
	ios::sync_with_stdio(false);
	int n;
	cin>>n;
	int w,u,v;
	for(int i=1;i<=n;i++){
		cin>>w>>u>>v;
		peo[i]=w;
		lchild[i]=u;
		rchild[i]=v;
		fa[u]=i;
		fa[v]=i;
	}
	int mind=1e9;
	for(int i=1;i<=n;i++){
		memset(vis,0,sizeof(vis));
		int sum=cal(i,0);
		if(sum<mind){
			mind=sum;
		}
	}
	cout<<mind<<endl;
	return 0;
}