平面向量内积坐标公式推导_第七讲：向量————一种有趣的数学工具

一、什么叫量。
量是为了衡量度量现象、物体或物质的特性而创造的概念。
以前我们学的量由表示大小的数字表示，只能表示其一个维度，即大小、高低等。
这样的量叫标量，可以进行加减乘除运算。
但是，生活中有一些量除了大小还有方向的特征，这样的量是不能简单的进行加减乘除运算的。
因此我们引入了一个新的概念：向量，用来表示这种特殊的有大小和方向的矢量，并研究它的运算法则。
为了方便理解向量的方向性，我们来看这样一个例子。举例：我们先往东跑400米，然后往北方向跑300米，我们现在的位置距离起点多远了？
是700米（300+400）吗？
显然不是，应该是500米。
这很普通是吗？没错，这很奇怪，在面对位置这样的问题，我们的量是不能直接数字相加的。二、引入符号系统表示向量。1.在下图中，线段可以表示线段的大小（长度），箭头可以表示方向。因此我们用有箭头的线段，这种可以表示方向又可以表示大小的方法来表示向量。如：

2.对于具体的向量如点A到点B的向量，我们表示为

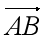
也可以简化为：下图的写法，在印刷题中为了方便表示可以用粗体小写字母表示，如a为了方便表示，下文中我们都用粗体小写字母表示向量。