算法数据结构——双指针

1，双指针的基本知识

双指针是一种应用很广泛且基础的编程技巧，双指针中的“指针”是指索引、游标。

1.1、双指针思想

双指针是指在遍历对象的过程中，不是普通的使用单个指针进行访问，而是使用两个指针进行遍历，从而达到相应的目的。

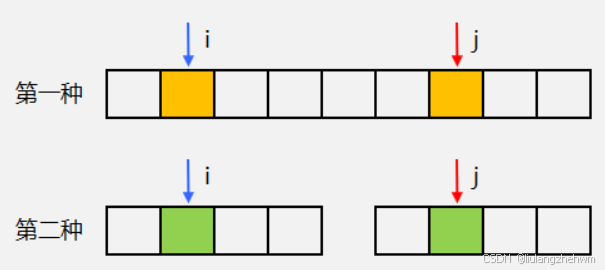
最常见的双指针算法有两种：

• 在同一个序列中，用两个指针维护两个位置，或两个位置包含的区间；
• 在两个序列里边，两个指针指向不同的序列，来维护某种次序。
  
  原文链接

2、例一（leetcode:11. 盛最多水的容器）

2.1，题目描述

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明：你不能倾斜容器。

示例 1：

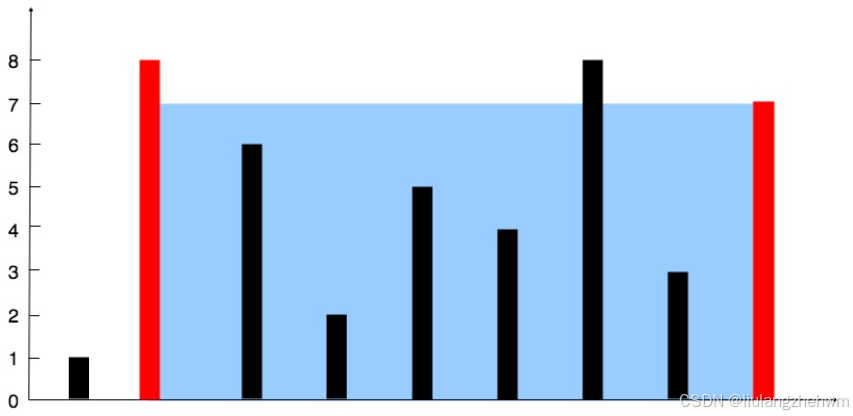
输入：[1,8,6,2,5,4,8,3,7]
输出：49
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：
输入：height = [1,1]
输出：1

2.2，解题思路

在每个状态下，无论长板或短板向中间收窄一格，都会导致水槽 底边宽度 −1​ 变短：

• 若向内 移动短板 ，水槽的短板 min(h[i],h[j]) 可能变大，因此下个水槽的面积 可能增大 。
• 若向内 移动长板 ，水槽的短板 min(h[i],h[j])​ 不变或变小，因此下个水槽的面积 一定变小 。

因此，初始化双指针分列水槽左右两端，循环每轮将短板向内移动一格，并更新面积最大值，直到两指针相遇时跳出；即可获得最大面积。

算法流程：

1. 初始化： 双指针 i , j 分列水槽左右两端；
2. 循环收窄： 直至双指针相遇时跳出；
   • 更新面积最大值 res ；
   • 选定两板高度中的短板，向中间收窄一格；
3. 返回值： 返回面积最大值 res 即可；

def maxArea(self, height: List[int]) -> int:
        i, j, res = 0, len(height) - 1, 0
        while i < j:
            if height[i] < height[j]:
                res = max(res, height[i] * (j - i))
                i += 1
            else:
                res = max(res, height[j] * (j - i))
                j -= 1
        return res

原文链接

3，例二（leetcode:18. 四数之和）

3.1，题目描述

给你一个由 n 个整数组成的数组 nums ，和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] （若两个四元组元素一一对应，则认为两个四元组重复）：

• 0 <= a, b, c, d < n
• a、b、c 和 d 互不相同
• nums[a] + nums[b] + nums[c] + nums[d] == target

你可以按 任意顺序 返回答案 。

示例 1：
输入：nums = [1,0,-1,0,-2,2], target = 0
输出：[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]

示例 2：
输入：nums = [2,2,2,2,2], target = 8
输出：[[2,2,2,2]]

3.2，解题思路

这道题和此前的三数之和很相似，只是多套了一层循环。可按以下步骤求解：

1. 先对数组排序。
2. 从左向右枚举 i
3. 固定 i，枚举 j，j>i
4. 在 (j,nums.size) 这个区间内使 l 和 r 双向滑动，求解满足元素和为 target 的四元组。

class Solution:
    def fourSum(self, nums: List[int], target: int) -> List[List[int]]:
        nums.sort()

        quadruples = [] # 四元组

        for i in range(len(nums)):
            if i > 0 and nums[i] == nums[i - 1]: continue

            for j in range(i + 1, len(nums)):
                if j > i + 1 and nums[j] == nums[j - 1]: continue

                l, r = j + 1, len(nums) - 1

                while l < r:
                    if r < len(nums) - 1 and nums[r] == nums[r + 1]:
                        r -= 1
                    elif l > j + 1 and nums[l] == nums[l - 1]:
                        l += 1
                    elif nums[i] + nums[j] + nums[l] + nums[r] > target:
                        r -= 1
                    elif nums[i] + nums[j] + nums[l] + nums[r] < target:
                        l += 1
                    else:
                        quadruples.append([nums[i], nums[j], nums[l], nums[r]])
                        l += 1; r -= 1

        return quadruples

原文链接