概率与信息论基础总结LAN

随机变量：
随机变量（random variable）是可以随机地取不同值的变量
就其本身而言，一个随机变量只是对可能的状态的描述；它必须伴随着一个概率分布来指定每个状态的可能性。

随机变量可以是离散的或者连续的。离散随机变量拥有有限或者可数无限多的
状态。注意这些状态不一定非要是整数；它们也可能只是一些被命名的状态而没有 数值。连续随机变量伴随着实数值。

概率分布：
概率分布（probability distribution）用来描述随机变量或一簇随机变量在每一个可能取到的状态的可能性大小。

我们描述概率分布的方式取决于随机变量是离散的还是连续的

离散型变量和概率质量函数：
离散型变量的概率分布可以用 概率质量函数（probability mass function, PMF） 来描述。
我们通常用大写字母 P 来表示概率质量函数。
通常每一个随机变量都会有一个不同的概率质量函数。
概率质量函数将随机变量能够取得的每个状态映射到随机变量取得该状态的概率。
x = x 的概率用 P(x) 来表示，概率为 1 表示 x = x 是确定的，概率为 0 表示x = x 是不可能发生的。

有时为了使得PMF的使用不相互混淆，我们会明确写出随 机变量的名称：P(x = x)。有时我们会先定义一个随机变量，然后用 ∼ 符号来说明
它遵循的分布：x ∼ P(x)。

概率质量函数可以同时作用于多个随机变量。
这种多个变量的概率分布被称为 联合概率分布（joint probability distribution）。
P(x = x, y = y) 表示 x = x 和 y = y 同时发生的概率。我们也可以简写为 P(x, y)。
如果一个函数 P 是随机变量 x 的 PMF，必须满足下面这几个条件：

1、P 的定义域必须是 x 所有可能状态的集合。
2、 ∀x ∈ x, 0 ≤ P(x) ≤ 1. 不可能发生的事件概率为 0，并且不存在比这概率更低的状态。类似的，能够确保一定发生的事件概率		 为 1，而且不存在比这概率更高的状态。
3、∑x∈x P(x) = 1. 我们把这条性质称之为 归一化的（normalized）。如果没有这条性质，当我们计算很多事件其中之一发生的概率时可能会得到大于 1 的概率。

连续型变量和概率密度函数：

边缘概率：

条件概率：

条件概率的链式法则：

独立性和条件独立性：


期望、方差和协方差：







Bernoulli 伯努利分布 （一枚硬币抛一次）：
Bernoulli 分布（Bernoulli distribution）是单个二值随机变量的分布。
伯努利分布 是一种离散分布,有两种可能的结果。
1表示成功，出现的概率为p(其中0<p<1)。
0表示失败，出现的概率为q=1-p。


二项分布（n重Bernoulli分布）（一枚硬币抛n次）：

多项分布 （一把硬币抛n次）：

范畴分布：

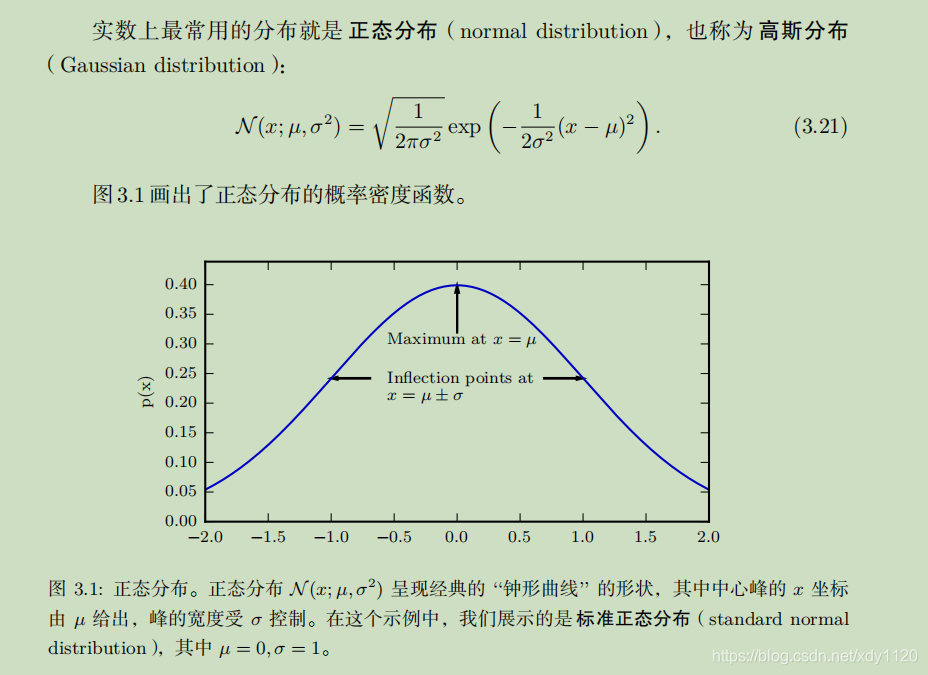
高斯分布：



指数分布和 Laplace 分布：

Dirac 分布和经验分布：

混合分布：



常用函数的有用性质：






贝叶斯：


结构化概率模型：