一、贝叶斯简介
朴素贝叶斯分类器用于计算可能条件的分支概率。每个独立的特征都是「朴素」或条件独立的,因此它们不会影响别的对象。例如,在一个装有共 5 个黄色和红色小球的罐子里,连续拿到两个黄色小球的概率是多少?从图中最上方分支可见,前后抓取两个黄色小球的概率为 1/10。朴素贝叶斯分类器可以计算多个特征的联合条件概率。
✅ 贝叶斯定理
根据先验概率和条件概率得到后验概率
✅ 朴素贝叶斯定理
在贝叶斯原理基础上,加了一个前提假设:所有的条件对结果都是独立发生作用的
✅ 条件概率
事件 B 在另一个事件 A 已经发生条件下的概率,记作 P(B|A)。
在统计学中,也称之为似然函数。
✅ 先验概率
事件 A 或 事件 B 是根据经验来判断发生的概率,记作 P(A)、P(B)。
✅后验概率
我们已经看到某个事情发生了,再判断这个事情发生原因的概率,即在事件已经发生后,推测原因。比如 P(A|B) 是已知 B 发生后 A 的条件概率,也叫做 A 的后验概率。
✅优点
算法的逻辑简单
不需要训练,算法计算的时候对资源占用比较小
✅缺点
使用非常有局限性,只有在条件比较少,并且相互独立的时候,朴素贝叶斯的效果才会比较好
✅应用场景
从算法场景来说,比较适合文本分类、情感分析、垃圾邮件分类这类场景,因为这些数据的相互独立性更高
从开发成本来说,适合项目周期比较紧张,算力资源不太充足的情况
垃圾邮件分类: 根据电子邮件的内容识别电子邮件是否为垃圾邮件
实时预测系统: 该模型相对较快,因此可以实时预测目标变量
情绪分析:识别产品的反馈并将其分类为“正面”或“负面”
二、条件概率
对条件概率公式进行变形,可以得到如下形式:
我们把P(A)称为"先验概率"(Prior probability),即在B事件发生之前,我们对A事件概率的一个判断。
P(A|B)称为"后验概率"(Posterior probability),即在B事件发生之后,我们对A事件概率的重新评估。
P(B|A)/P(B)称为"可能性函数"(Likelyhood),这是一个调整因子,使得预估概率更接近真实概率。
所以,条件概率可以理解成式子:后验概率 = 先验概率 x 调整因子
三、朴素贝叶斯推断
理解了贝叶斯推断,那么让我们继续看看朴素贝叶斯。贝叶斯和朴素贝叶斯的概念是不同的,区别就在于“朴素”二字,朴素贝叶斯对条件个概率分布做了条件独立性的假设。 比如下面的公式,假设有n个特征:
由于每个特征都是独立的,我们可以进一步拆分公式 :
法国数学家拉普拉斯最早提出用加1的方法估计没有出现过的现象的概率。 拉普拉斯平滑处理后的条件概率计算公式为:
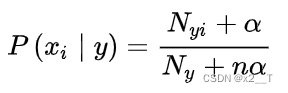
四、动手实践
import numpy as np
"""
函数功能:创建实验数据集
参数说明:无参数
返回:
postingList:切分好的样本词条
classVec:类标签向量
"""
def loadDataSet(): #loadDataSet:创建实验数据集
dataSet=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
['stop', 'posting', 'stupid', 'worthless', 'garbage'],
['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']] #切分好的词条
classVec = [0,1,0,1,0,1] #类别标签向量,1代表侮辱性词汇,0代表非侮辱性词汇
return dataSet,classVec
dataSet,classVec=loadDataSet()
"""
函数功能:将切分的样本词条整理成词汇表(不重复)
参数说明:
dataSet:切分好的样本词条
返回:
vocabList:不重复的词汇表
"""
def createVocabList(dataSet):
vocabSet = set() #创建一个空的集合
for doc in dataSet: #遍历dataSet中的每一条言论
vocabSet = vocabSet | set(doc) #取并集
vocabList = list(vocabSet)
return vocabList
vocabList = createVocabList(dataSet)
"""
函数功能:根据vocabList词汇表,将inputSet向量化,向量的每个元素为1或0
参数说明:
vocabList:词汇表
inputSet:切分好的词条列表中的一条
返回:
returnVec:文档向量,词集模型
"""
def setOfWords2Vec(vocabList, inputSet):
returnVec = [0] * len(vocabList) #创建一个其中所含元素都为0的向量
for word in inputSet: #遍历每个词条
if word in vocabList: #如果词条存在于词汇表中,则变为1
returnVec[vocabList.index(word)] = 1
else:
print(f" {word} is not in my Vocabulary!" )
return returnVec #返回文档向量
"""
函数功能:生成训练集向量列表
参数说明:
dataSet:切分好的样本词条
返回:
trainMat:所有的词条向量组成的列表
"""
def get_trainMat(dataSet):
trainMat = [] #初始化向量列表
vocabList = createVocabList(dataSet) #生成词汇表
for inputSet in dataSet: #遍历样本词条中的每一条样本
returnVec=setOfWords2Vec(vocabList, inputSet) #将当前词条向量化
trainMat.append(returnVec) #追加到向量列表中
return trainMat
trainMat = get_trainMat(dataSet)
def trainNB(trainMat,classVec):
n = len(trainMat) #计算训练的文档数目
m = len(trainMat[0]) #计算每篇文档的词条数
pAb = sum(classVec)/n #文档属于侮辱类的概率
p0Num = np.zeros(m) #词条出现数初始化为0
p1Num = np.zeros(m) #词条出现数初始化为0
p0Denom = 0 #分母初始化为0
p1Denom = 0 #分母初始化为0
for i in range(n): #遍历每一个文档
if classVec[i] == 1: #统计属于侮辱类的条件概率所需的数据
p1Num += trainMat[i]
p1Denom += sum(trainMat[i])
else: #统计属于非侮辱类的条件概率所需的数据
p0Num += trainMat[i]
p0Denom += sum(trainMat[i])
p1V = p1Num/p1Denom
p0V = p0Num/p0Denom
return p0V,p1V,pAb #返回属于非侮辱类,侮辱类和文档属于侮辱类的概率
p0V,p1V,pAb = trainNB(trainMat, classVec)




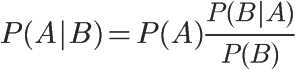
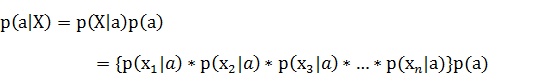
















 596
596










