
持续分享:机器学习、深度学习、python相关内容、日常BUG解决方法及Windows&Linux实践小技巧。
如发现文章有误,麻烦请指出,我会及时去纠正。有其他需要可以私信我或者发我邮箱:zhilong666@foxmail.com
朴素贝叶斯算法是一种基于贝叶斯定理的分类算法,它利用先验概率和条件概率推导出后验概率,从而进行分类。该算法被广泛应用于自然语言处理、垃圾邮件过滤和文本分类等领域,并且在很多数据挖掘竞赛中获得了优秀的结果。Python版本的朴素贝叶斯算法也被广泛使用,由于其易于实现和高效性能,成为了数据科学家和机器学习工程师的首选算法之一。
本文将详细讲解机器学习十大算法之一 “朴素贝叶斯”

目录
一、简介
朴素贝叶斯算法是一种监督学习的算法,通过计算条件概率来预测或分类数据。它的核心思想是贝叶斯定理,即后验概率等于先验概率与似然函数的乘积除以证据因子。
在文本分类的应用中,假设我们有一个文档和一个文档分类,我们想要判断这个文档属于哪个分类。我们可以将文档中的每个词都看作一个特征,每个特征的值为 0 或 1,0 表示该词不在文档中,1 表示该词在文档中。这样,我们就可以将每个文档表示为一个特征向量。然后,我们可以使用朴素贝叶斯算法来计算每个分类的条件概率,并选择条件概率最大的分类作为文档所属的分类。
二、发展史
朴素贝叶斯算法最早可以追溯到18世纪的贝叶斯学派。但是,直到20世纪60年代,才有了将贝叶斯方法用于文本分类的尝试。最早的一篇文献是由Thomas Bayes的朋友Richard Price在1763年发表的《An Essay towards solving a Problem in the Doctrine of Chance》。它提出了贝叶斯规则,构成了朴素贝叶斯算法的核心。
在20世纪60年代,刚刚问世的计算机开始被广泛使用,使得大规模文本分类成为可能。此时,发展起了文本分类领域的先驱性研究,G. Salton 等人提出了矢量空间模型和 TF-IDF 权重算法,但是它们都依赖于一个主题词典或类别词汇表。
直到20世纪80年代,朴素贝叶斯算法成为文本分类中最重要的方法之一。 Paul Dressel 和 Donald Bienenstock 的著名论文《SVMs and the Bayes Kernel》中,他们通过 SVM 与朴素贝叶斯算法的比较得出,朴素贝叶斯算法相对于 SVM 算法有着更高的准确率。
现在,朴素贝叶斯算法已经成为自然语言处理领域中最常用的算法之一。
三、算法原理、功能讲解
朴素贝叶斯算法是一种基于概率论和统计学的算法。它的核心思想是概率,通过计算条件概率来预测或分类数据。在此之前,我们需要了解一下几个与朴素贝叶斯算法相关的概念。
1. 贝叶斯定理
贝叶斯定理是朴素贝叶斯算法的核心,它是一个概率公式,用于计算一个事件的后验概率。根据贝叶斯定理,事件 A 的后验概率等于先验概率 P(A),与另一个事件 B 发生的联合概率 P(B|A) 乘以一个正则因子,即:
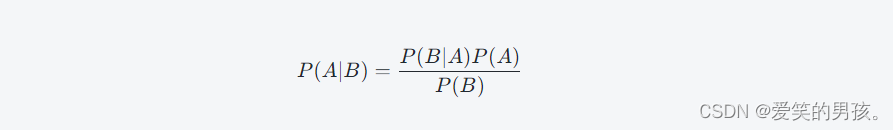
其中,P(A) 和 P(B) 是事件 A 和事件 B 的先验概率,P(B|A) 是给定事件 A 发生的情况下事件 B 发生的条件概率,P(A|B) 是在事件





 本文详细介绍了朴素贝叶斯算法的原理、发展史、Python实现步骤以及优缺点。通过使用scikit-learn库展示了如何在文本分类问题上应用该算法,并通过示例代码展示了如何训练和评估模型的准确性。
本文详细介绍了朴素贝叶斯算法的原理、发展史、Python实现步骤以及优缺点。通过使用scikit-learn库展示了如何在文本分类问题上应用该算法,并通过示例代码展示了如何训练和评估模型的准确性。
 https://blog.youkuaiyun.com/Code_and516?type=blog
https://blog.youkuaiyun.com/Code_and516?type=blog 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 605
605

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










