序列中位数

原创已于 2025-04-15 01:29:41 修改 · 985 阅读

14 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c++

于 2025-04-15 01:27:39 首次发布

最近找实习被狠狠笔试拷打了😭，现在看来还是基础不扎实，题是写了，但是没有复盘总结，不久就忘了，我决定开一个新的小专栏来记录和分析我写过的算法题。先从腾讯23年秋招的一道题目开始吧！链接在这里

先来看看题目：

题目描述

牛牛有一个长度为 n 的整数序列 a，以及一个长度为 n - 1 的整数序列 b，其中 b 中的元素各不相同。牛牛会首先计算序列 a 的中位数，然后按照序列 b 的顺序，依次删除原序列 a 中对应位置的元素，即删除 a[b[i]]，其中 0 <= i < n - 1。每次删除后，牛牛会重新计算序列 a 中剩余元素的中位数。

若剩余元素数量为奇数，则中位数为排序后中间的那个数。
若剩余元素数量为偶数，则中位数为排序后中间两个数的平均值。

牛牛将每次计算得到的中位数记录下来，但担心出现错误。请你帮助他验证结果是否正确。

输入描述

第一行输入一个整数 t（1 <= t <= 10），表示数据组的数量。对于每组数据，输入三行：

第一行为一个整数 n（1 <= n <= 10000），表示序列的长度。
第二行为 n 个整数，表示序列 a 的元素（1 <= a[i] <= 10^9）。
第三行为 n - 1 个整数，表示序列 b 的元素（1 <= b[i] < n）。

输出描述

对于每组数据，输出一行，包含 n 个数，表示每次删除后的中位数结果。

如果中位数是浮点数，则保留一位小数。
如果中位数是整数，则直接输出整数。

方法一：直接删除

解题思路

唔，刚开始看到这道题目很容易想到直接删除数组元素，但这样的时间复杂度有点高，代码如下：

#include <bits/stdc++.h>

using namespace std;

#define endl '\n'

// 计算并返回中位数
double findMedian(vector<int>& nums) {
    int n = nums.size();
    if (n % 2 == 1) {
        return nums[n / 2]; // 奇数长度，返回中间的元素
    } else {
        // 偶数长度，返回中间两个元素的平均值
        return (nums[n / 2] + nums[n / 2 - 1]) / 2.0;
    }
}

int main(){
    int t;
    cin >> t;
    while(t--){
        int n;
        cin>> n;
        vector<int> a(n);
        vector<int> b(n - 1);
        for(int i = 0; i < n; i++){
            cin >> a[i];
        }
        for(int i = 0; i < n - 1; i++){
            cin >> b[i];
        }
        vector<int> nums = a;
        vector<double> answers; 
        
        sort(nums.begin(), nums.end());
      
        // 把中位数放进结果集
        answers.push_back(findMedian(nums));

        for(int i = 0; i < n - 1; i++){ 
            
            int target = a[b[i]];
            // 删除目标值
            nums.erase(find(nums.begin(), nums.end(), target));
            // 把中位数放进结果集
            answers.push_back(findMedian(nums));

        }

        for(auto answer : answers){  
            // 判断是否是整数
            if(answer == (int)answer) printf("%d ", (int)answer);
            else printf("%.1f ", answer);
        }
        cout << endl;
    }
}

复杂度分析

时间复杂度：因为移除数组中元素的时间复杂度为 O(n)，故总时间复杂度为 O(t * n^2) 勉强通过

空间复杂度：因为使用了数组，O(n)

方法二：multiset 模拟

解题思路

使用两个 multiset 分别保存排序后的数组平分后的左右部分，当剩余的数字为奇数时保证右数组的大小比左数组大1，若为偶数保证左右数组的大小相等。

在决定移除左数组还是右数组中的元素时，可以参考前一次的中位数，若要移除的数比前一次的中位数大，说明要移除的数在右数组中，则移除右数组中的元素，反之移除左数组的元素。

如果前一次的中位数和现在要移除的数相等，还是移除右数组中的元素，为什么呢？我们接着来分析：

如果前一次的移除元素完成后的数组为奇数，那么中位数就是我们现在要移除的元素了，也可能有多个与现在要移除的元素相等的元素，但是我们保证右数组的大小始终大于左数组的大小，所以一定会有至少一个要移除的元素在右数组内，也就是移除右数组中的元素是可行的，如下图所示：

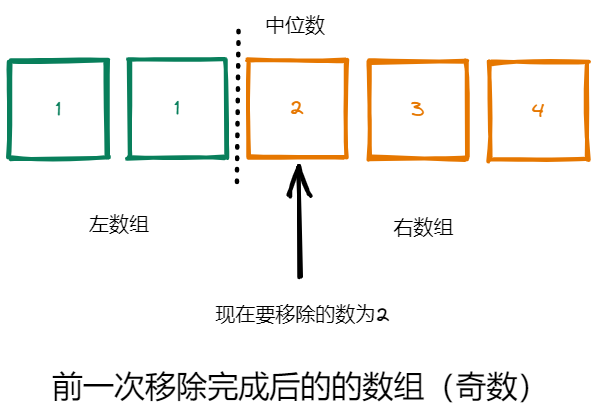
如果前一次移除完成后的数组为偶数，那么前一次移除完成后的数组中一定至少有一个现在要移除的元素。为什么不会是两个加起来和为现在要移除的元素的大小两倍的元素呢？因为我们得到的是排序后的数组，而且现在要移除的元素一定在数组内，所以不可能出现比要移除的元素大和小的元素紧挨着的情况。也就是说，如果要出现前一次移除完成后的数组为偶数，且中位数与现在要移除的元素相等的情况，那么一定至少有两个元素的大小和现在要移除的元素大小相等。所以还是一定会有至少一个要移除的元素在右数组内，如下图所示：

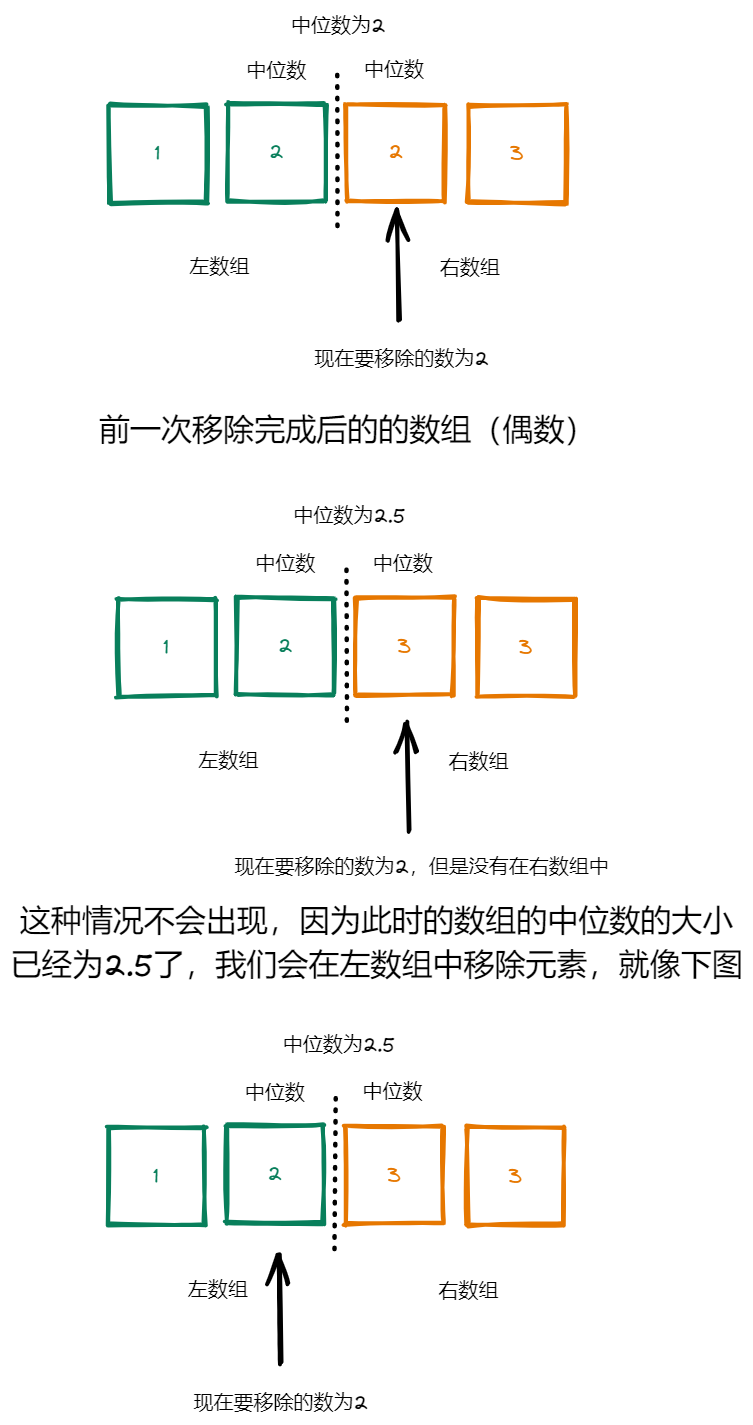
所以综上所述，如果前一次的中位数和现在要移除的数相等，还是移除右数组中的元素。

注意要使用迭代器移除元素，这样不会将所有相同的元素移除。代码如下：

#include <bits/stdc++.h>

using namespace std;

#define endl '\n'

// 使用两个multiset分别维护数组的左右两部分：
// leftNums：降序排列，存储较小的一半元素（可快速获取最大值）
// rightNums：升序排列，存储较大的一半元素（可快速获取最小值）
multiset<int, greater<int>> leftNums; 
multiset<int> rightNums;

// 计算当前中位数
double findMedian() {
  double result = 0;

  // 当元素总数为奇数时，中位数为元素较多的集合的首元素
  if (leftNums.size() != rightNums.size()) {
    if (rightNums.size() > leftNums.size()) {
      result = *rightNums.begin(); // 右半部分的最小值
    } else {
      result = *leftNums.begin(); // 左半部分的最大值
    }
  } 
  // 当元素总数为偶数时，中位数为两个集合首元素的平均值
  else { 
    result = *leftNums.begin() + (*rightNums.begin() - *leftNums.begin()) / 2.0;
  }

  return result;
}

int main() {
  int t;
  cin >> t;

  while (t--) {
    leftNums.clear();
    rightNums.clear();

    int n;
    cin >> n;

    vector<int> a(n);
    vector<int> b(n - 1);

    // 读取初始数组
    for (int i = 0; i < n; i++) {
      cin >> a[i];
    }

    // 读取删除顺序数组（保存要删除的索引）
    for (int i = 0; i < n - 1; i++) {
      cin >> b[i];
    }

    vector<int> nums(a);       // 创建可修改的数组副本
    vector<double> answers;    // 保存每个步骤的中位数结果

    // 初始排序以分割左右部分
    sort(nums.begin(), nums.end());

    // 将排序后的数组均分到左右集合
    for (int i = 0; i < nums.size() / 2; i++) {
      leftNums.insert(nums[i]); // 较小的一半存入左集合
    }
    for (int i = nums.size() / 2; i < nums.size(); i++) {
      rightNums.insert(nums[i]); // 较大的一半存入右集合
    }

    // 记录初始中位数
    answers.push_back(findMedian());

    // 处理每个删除操作
    for (int i = 0; i < n - 1; i++) {
      // 根据当前中位数判断被删除元素属于哪个集合
      if (answers[i] > a[b[i]]) { 
        // 当元素小于中位数时，应从左集合删除
        auto it = leftNums.find(a[b[i]]);
        if (it != leftNums.end()) {
          leftNums.erase(it);
        }
      } else {
        // 当元素大于等于中位数时，从右集合删除
        auto it = rightNums.find(a[b[i]]);
        if (it != rightNums.end()) {
          rightNums.erase(it);
        }
      }

      int total = leftNums.size() + rightNums.size();

      // 调整左右集合的平衡，确保大小差不超过1
      if (leftNums.size() > total / 2) { 
        // 左集合元素过多，移动最大值到右集合
        rightNums.insert(*leftNums.begin());
        leftNums.erase(leftNums.begin());
      }
      if (leftNums.size() < total / 2) {
        // 右集合元素过多，移动最小值到左集合
        leftNums.insert(*rightNums.begin());
        rightNums.erase(rightNums.begin());
      }

      // 计算新的中位数并记录
      answers.push_back(findMedian());
    }

    // 格式化输出结果
    for (auto answer : answers) {
      if (answer == (int)answer) {
        printf("%d ", (int)answer); // 整数输出
      } else {
        printf("%.1f ", answer);    // 保留一位小数
      }
    }
    cout << endl;
  }
  return 0;
}

当然了，如果我们始终保证左数组中的元素数量始终大于等于右数组中的，这是我们在相等时就要移除左数组中的元素了。

但是要注意：初始化分割数组时要将数组大小加1再除以2，为了保证左数组的大小大于等于右数组的大小。

代码如下：

#include <bits/stdc++.h>

using namespace std;

#define endl '\n'
// 使用两个multiset维护有序数组的左右两部分
// leftNums: 降序排列，存储较小的一半元素（允许快速获取最大值）
// rightNums: 升序排列，存储较大的一半元素（允许快速获取最小值）
multiset<int, greater<int>> leftNums;
multiset<int> rightNums;

// 计算当前中位数
double findMedian() {
  double result = 0;

  // 当元素总数是奇数时，中位数为元素较多的集合的首元素
  if (leftNums.size() != rightNums.size()) {
    // 通过比较集合大小确定中位数位置
    if (leftNums.size() > rightNums.size()) {
      result = *leftNums.begin();  // 左半部分的最大值
    } else {
      result = *rightNums.begin(); // 右半部分的最小值
    }
  } 
  // 当元素总数是偶数时，中位数为两集合首元素的平均值
  else {
    result = *leftNums.begin() + (*rightNums.begin() - *leftNums.begin()) / 2.0;
  }

  return result;
}

int main() {
  int t;
  cin >> t;

  while (t--) {
    leftNums.clear();
    rightNums.clear();

    int n;
    cin >> n;

    vector<int> a(n);
    vector<int> b(n - 1);

    // 读取初始数组元素
    for (int i = 0; i < n; i++) {
      cin >> a[i];
    }

    // 读取删除顺序数组（注意存储的是索引值）
    for (int i = 0; i < n - 1; i++) {
      cin >> b[i];
    }

    vector<int> nums(a);    // 创建可修改的数组副本
    vector<double> answers; // 存储各阶段的中位数结果

    // 初始排序以分割左右部分
    sort(nums.begin(), nums.end());

    /* 关键修改点1：初始化分割策略改变 */
    // 将数组分割为左大右小的两部分：
    // - 左半部分包含前 (n+1)/2 个元素（奇数时左半多1个元素）
    // - 保证初始中位数可以直接从leftNums获取
    for (int i = 0; i < (nums.size() + 1) / 2; i++) {  
      leftNums.insert(nums[i]); // 较小的一半存入左集合
    }  
    for (int i = (nums.size() + 1) / 2; i < nums.size(); i++) {  
      rightNums.insert(nums[i]); // 较大的一半存入右集合
    }

    // 记录初始中位数
    answers.push_back(findMedian());

    // 处理每个删除操作
    for (int i = 0; i < n - 1; i++) {
      /* 关键修改点2：删除条件判断改变（>= 替代 >）*/
      // 根据当前中位数判断元素归属集合：
      // - 当元素值 <= 当前中位数时，从左集合删除
      // - 当元素值 > 当前中位数时，从右集合删除
      if (answers[i] >= a[b[i]]) { 
        auto it = leftNums.find(a[b[i]]);
        if (it != leftNums.end()) {
          leftNums.erase(it); // 从左集合安全删除
        }
      } else {
        auto it = rightNums.find(a[b[i]]);
        if (it != rightNums.end()) {
          rightNums.erase(it); // 从右集合安全删除
        }
      }

      int total = leftNums.size() + rightNums.size();

      /* 关键修改点3：平衡逻辑改为优先调整右集合 */
      // 再平衡策略：确保两集合大小差不超过1
      if (rightNums.size() > total / 2) {
        // 右集合元素过多，移动最小值到左集合
        leftNums.insert(*rightNums.begin());
        rightNums.erase(rightNums.begin());
      }

      if (rightNums.size() < total / 2) {
        // 左集合元素过多，移动最大值到右集合
        rightNums.insert(*leftNums.begin());
        leftNums.erase(leftNums.begin());
      }

      // 计算并记录新的中位数
      answers.push_back(findMedian());
    }

    // 格式化输出结果
    for (auto answer : answers) {
      // 根据是否为整数决定输出格式
      if (answer == (int)answer)
        printf("%d ", (int)answer); // 整数输出
      else
        printf("%.1f ", answer);     // 保留一位小数
    }
    cout << endl;
  }
  return 0;
}

复杂度分析

时间复杂度：每个插入和删除操作在 multiset 中为O(log n)，每次调整操作的时间复杂度为O(log n)，总时间复杂度为O( t * n log n)。

空间复杂度：使用两个 multiset 存储元素，空间复杂度为O(n)。