三分(解决二次函数极值的问题，也就是单峰的问题）

三分的模板
这里的是 下凸函数

//check函数根据题目要求写
while(l <= r) {
	int midl = l + (r - l) / 3;
	int midr = r - (r - l) / 3;
	if(check(midl) <= check(midr)) r = midr - 1;
	else l = midl + 1;
}
res = min(check(r), check(l));

抓拍杭电oj
准确的说，这是我遇到的第一个三分的题目。需要求解的周长 y 和时间 x 构成函数，并且函数是 向上开口的 类似抛物线的图形。存在极小值点。我们就可以通过三分求极值。

#include <bits/stdc++.h>
#define int long long 
using namespace std;
const int N=2e5+5;
const int inf=1e12;
struct node {
    int x,y,d;
}a[N];
int dd[4][2]={ {0,1},{1,0},{0,-1},{-1,0}};
int n;
int check(int t)
{
枚举每一个点，一开始想的是，开四个数组，存放四个方向对应的x或者 y。check 的时候四个for 来确定最大最小的 x y.
但是这样做，例如 求 y的时候，最值可能是 一个并不向上下移动的点。这样会导致错误。所以必须要枚举所有的点。通过dd 数组 ，十分便捷的实现了每个时间 所有点的 坐标。  好美丽的代码，好喜欢~~
    int maxx=-inf,minx=inf;
    int maxy=-inf,miny=inf;
    for (int i=0;i<n;i++)
    {
        maxx=max(maxx,a[i].x+t*dd[a[i].d][0]);
        minx=min(minx,a[i].x+t*dd[a[i].d][0]);
        maxy=max(maxy,a[i].y+t*dd[a[i].d][1]);
        miny=min(miny,a[i].y+t*dd[a[i].d][1]);
    }
    return 2*(maxx-minx+maxy-miny);
}
void solve()
{
   cin>>n;
    for (int i=0;i<n;i++)
    {
        cin>>a[i].x>>a[i].y;
        char t;cin>>t;
        if (t=='N')a[i].d=0;
        else if (t=='E') a[i].d=1;
        else if (t=='S')a[i].d=2;
        else a[i].d=3;
    }
    
    int l=0,r=2e9;
    while(l<=r)
    {
        int midl=l+(r-l)/3;
        int midr=r-(r-l)/3;
        if (check(midl)<=check(midr))r=midr-1;
        else l=midl+1;
    }
    cout<<check(l)<<"\n";
        //cout<<min(check(l),check(r))<<"\n";
       
    
}
signed  main()
{
    std::cin.tie(nullptr)->sync_with_stdio(false);
    int t; t=1;
    //cin>>t;
    while(t--)
    {
        solve();
    }
    return 0;
}

5201
**
**
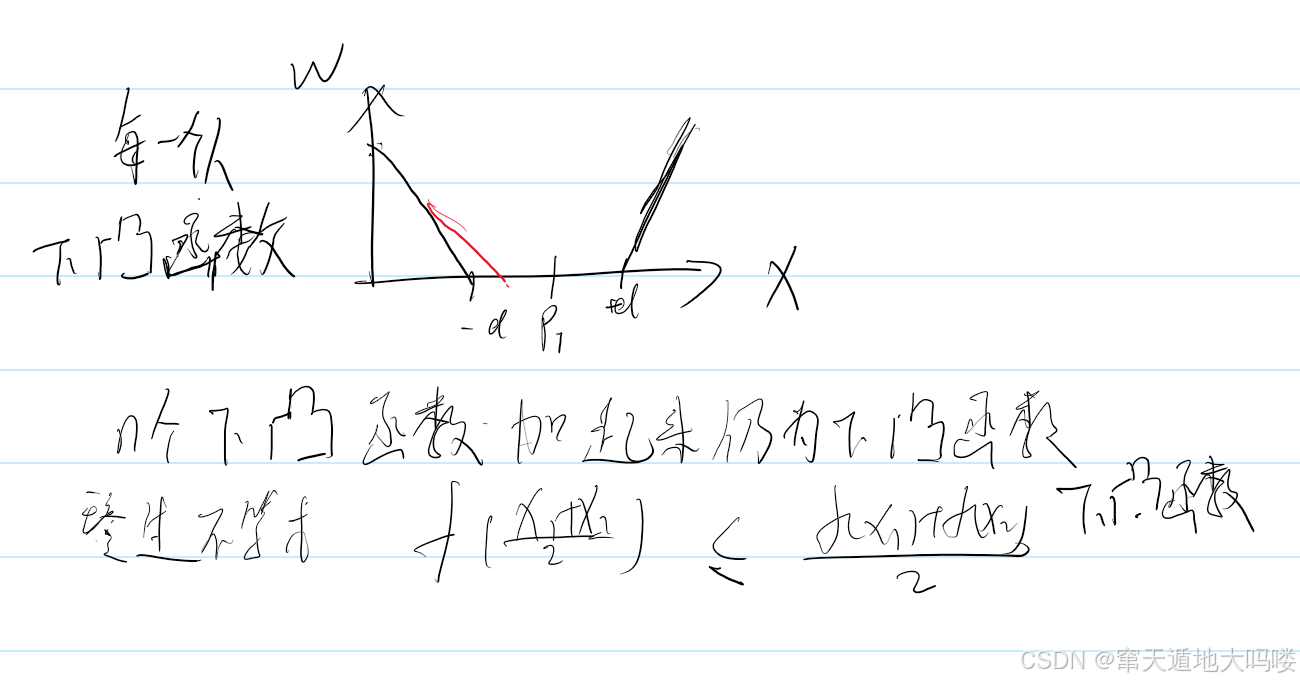
所以我们可以三分 演唱会的地方。check的时候，计算每一个人的w。nlogn的复杂度

#include <bits/stdc++.h>
#define int long long 
using namespace std;
const int N=2e5+10;
struct node{
    int p,w,d;
}a[N];
int n;
int check(int mid)
{
    int ans=0;
    for (int i=0;i<n;i++){
        int pos=a[i].p;
        int co=a[i].w;
        int dd=a[i].d;
        if (mid<=pos+dd&&mid>=pos-dd)continue;
        if (mid<pos) ans+=(pos-dd-mid)*co;
        else ans+=(mid-pos-dd)*co;
    }
    return ans;
}
void solve()
{
    cin>>n;
    int p,w,d;
    for (int i=0;i<n;i++){
        cin>>a[i].p>>a[i].w>>a[i].d;
    }
    //三分枚举位置
    int l=0,r=1e9;
    while(l<=r){
        int midl=l+(r-l)/3;
        int midr=r-(r-l)/3;
        if (check(midl)<=check(midr))r=midr-1;
        else l=midl+1;
    }
    cout<<min(check(r),check(l))<<endl;
}
signed  main()
{
    std::cin.tie(nullptr)->sync_with_stdio(false);
    int t; //cin>>t;
    t=1;
    while(t--)
    {
        solve();
    }
    return 0;
}

最近几天，人们总是设计出多功能的新东西。例如，您不仅可以使用手机给朋友打电话，还可以使用手机拍照或听MP3。另一个例子是手表和电视的结合。这些多功能项目总能改善人们的日常生活，深受用户青睐。

Umbrella公司最近为彩虹城的人们发明了一种新型伞“UmBasketella”，它的想法也来自于这种多功能 - 伞和日用品的组合。这种伞可以用作篮子，你可以放入你想要携带的东西。由于彩虹城经常下雨，这种创新用途是成功的，“UmBasketella”卖得很好。不幸的是，最初的“UmBasketella”没有自动音量控制技术，因此当用户试图在其中放入太多东西时很容易损坏。要解决这个问题，您需要设计一个具有最大音量的“UmBasketella”。假设“UmBasketella”是一个锥形容器，其表面区域（包括底部）是已知的，

输入

输入包含几个测试用例。Eash案例仅包含一个实数S，表示锥体的表面积。这是保证1≤ 小号 ≤10000。

产量

对于每个测试用例，输出应包含三行。
第一行应该有一个实数表示锥体的最大体积。
输出第二条线上锥体的高度和第三条线上锥体底部区域的半径。
所有实数都应该舍入到0.01。

样本输入

三十
样本输出

10.93
4.37
1.55

这道题，可以直接使用推导 ，用 r表示v.求导，之后就有了 r 。然后可以求的h 和最大的v.

#include <bits/stdc++.h>
using namespace std;
const double pi=3.1415926; 
int main()
{
	double s;cin>>s;
	double r=sqrt(s/(4*pi));
	double l=s/(pi*r)-r;
	double h=sqrt(s*s/(pi*pi*r*r)-2*s*r/(pi*r));
	double v=pi*r*r*h/3;
	printf("%0.2lf\n",v);
	printf("%0.2lf\n",h);
	printf("%0.2lf\n",r);
	return 0;
 } 

当然如果不想推导，也可以使用三分去做。

但是 如果使用三分的话，也要推导出来 v和 r的关系。看出来了是一个开口向下的函数。这样去三分 最大值。
个人感觉都推到这一步了，不如直接求导。