Python之背包问题

1.、问题描述

• 假设我们有n件物品，分别编号为1, 2…n。其中编号为i的物品价值为vi，它的重量为wi。为了简化问题，假定价值和重量都是整数值。现在，假设我们有一个背包，它能够承载的重量是W。现在，我们希望往包里装这些物品，使得包里装的物品价值最大化，那么我们该如何来选择装的东西呢？

• 这个问题其实根据不同的情况可以归结为不同的解决方法。假定我们这里选取的物品每个都是独立的，不能选取部分。也就是说我们要么选取某个物品，要么不能选取，不能只选取一个物品的一部分。这种情况，我们称之为0-1背包问题。而如果我们可以使用部分的物品的话，这个问题则成为部分背包(fractional knapsack)问题。下面我们针对每种情况具体分析一下。

1.1、0-1背包问题

1.1.1、动态规划

我们需要选择n个元素中的若干个来形成最优解，假定为k个。那么对于这k个元素a1, a2, …ak来说，它们组成的物品组合必然满足总重量<=背包重量限制，而且它们的价值必然是最大的。因为它们是我们假定的最优选择嘛，肯定价值应该是最大的。假定ak是我们按照前面顺序放入的最后一个物品。它的重量为wk，它的价值为vk。既然我们前面选择的这k个元素构成了最优选择，如果我们把这个ak物品拿走，对应于k-1个物品来说，它们所涵盖的重量范围为0-(W-wk)。假定W为背包允许承重的量。假定最终的价值是V，剩下的物品所构成的价值为V-vk。这剩下的k-1个元素是不是构成了一个这种W-wk的最优解呢？

我们可以用反证法来推导。假定拿走ak这个物品后，剩下的这些物品没有构成W-wk重量范围的最佳价值选择。那么我们肯定有另外k-1个元素，他们在W-wk重量范围内构成的价值更大。如果这样的话，我们用这k-1个物品再加上第k个，他们构成的最终W重量范围内的价值就是最优的。这岂不是和我们前面假设的k个元素构成最佳矛盾了吗？所以我们可以肯定，在这k个元素里拿掉最后那个元素，前面剩下的元素依然构成一个最佳解。

现在我们经过前面的推理已经得到了一个基本的递推关系，就是一个最优解的子解集也是最优的。可是，我们该怎么来求得这个最优解呢？我们这样来看。假定我们定义一个函数c[i, w]表示到第i个元素为止，在限制总重量为w的情况下我们所能选择到的最优解。那么这个最优解要么包含有i这个物品，要么不包含，肯定是这两种情况中的一种。如果我们选择了第i个物品，那么实际上这个最优解是c[i - 1, w-wi] + vi。而如果我们没有选择第i个物品，这个最优解是c[i-1, w]。这样，实际上对于到底要不要取第i个物品，我们只要比较这两种情况，哪个的结果值更大不就是最优的么？

在前面讨论的关系里，还有一个情况我们需要考虑的就是，我们这个最优解是基于选择物品i时总重量还是在w范围内的，如果超出了呢？我们肯定不能选择它，这就和c[i-1, w]一样。

另外，对于初始的情况呢？很明显c[0, w]里不管w是多少，肯定为0。因为它表示我们一个物品都不选择的情况。c[i, 0]也一样，当我们总重量限制为0时，肯定价值为0。

这样，基于我们前面讨论的这3个部分，我们可以得到一个如下的递推公式：

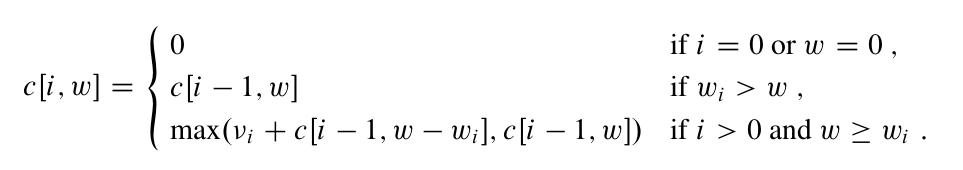
有了这个关系，我们可以更进一步的来考虑代码实现了。我们有这么一个递归的关系，其中，后面的函数结果其实是依赖于前面的结果的。我们只要按照前面求出来最基础的最优条件，然后往后面一步步递推，就可以找到结果了。

我们再来考虑一下具体实现的细节。这一组物品分别有价值和重量，我们可以定义两个列表v和w。v[i]表示第i个物品的价值，w[i]表示第i个物品的重量。为了表示x[i, j]，我们可以使用一个x[i,j]的矩阵。其中i的最大值为物品的数量，而j表示最大的重量限制。按照前面的递推关系，x[i,0]和x[0,j]都是0。而我们所要求的最终结果是x[n,c]，其中c表示问题中背包的载重量，n表示问题中物品的数量。所以我们实际中创建的矩阵是(n + 1) x (c + 1)的规格。下面是该过程的一个代码参考实现：

w = [0,2,3,4,5]  #物品重量（前面的0是为了从0递推）
v = [0,3,4,5,6]  #物品价值  （前面的0是为了从0递推）

n = 4    #物品数量
c = 8   # 背包的总载重量

import numpy as np

x = np.zeros([n+1,c+1])  # 建立n+1 * c+1维的矩阵

for i in range(1,n+1):   矩阵中的第i行表示在不同载重量情况下对前i个物品的最优选择
    for j in range(c,0,-1):  矩阵的每一列表示在载重量相同的情况下，取不同数量的物品的最优选择
        if j < w[i]:  # 如果要选择的物品的重量比载重量还重，那肯定不选取，最优解仍然是i-1下的j
            x[i,j] = x[i-1,j]
        else:#如果可以选，则要看选了之后的总价值比没选的总价值进行比较，选最大的
            x[i,j] = max(x[i-1,j],x[i-1,j-w[i]]+v[i])

1.2、132. Palindrome Partitioning II

该问题中，动态规划状态转移的方式是：

1. 设dp[i]为前i个字符串的最小分割，设0<=j<=i，那么，如果j至i的字符串s[j:i+1]为回文，则能够找到最小的分割为：在dp[j-1]的基础上+1；

注意，可能存在多个j使s[j:i+1]为回文，所以，使回文成立的各个j得到的dp[j-1]+1在更新dp[i]前，需要和dp[i]（dp[i]初始值为i-1，因为对于i个元素，最多有i-1个分割）不断比较，以将dp[i]更新为最小值，最终得到最小分割dp[i]

• 因此，递推公式为：dp[i]=min(dp[i],dp[j-1]+1) 循环条件：for j in range(i+1): if s[j:i+1]为回文

另外，关于判断s[j:i+1]是否为回文，还能用到动态规划，状态转移的方式是：

1. 设p[j][i]为s[j:i+1]是否为回文的标记；
2. 首先判断s[j] == s[i]，若否就肯定不是回文
3. 若是，且p[j+1][i-1]为回文或者满足j>i-2(意思是i和j相差1或i=j的情况下，如"aa"（因为i和j相差1，又满足s[j] == s[i]，所以是回文）和"a"（此时i=j，满足s[j] == s[i]，必定是回文）)
4. 则p[i][j]明显为回文

• 因此，递推公式为if s[j] == s[i] and (j>i-2 or isPal[j+1][i-1]): isPal[j][i] = True

class Solution(object):
    def minCut(self, s):
        """
        :type s: str
        :rtype: int
        """
        
        n = len(s)
        
        dp = [0 for __ in range(n)]
        
        isPal = [[False for __ in range(n)] for __ in range(n)]
        
        for i in range(n):
            m = i
            for j in range(i+1):
                if s[j] == s[i] and (j>i-2 or isPal[j+1][i-1]): # 判断是否回文也是动态回归
                    isPal[j][i] = True
                    if j == 0:
                        m = 0
                    else:
                        m = min(m,dp[j-1]+1)  # 这也是动态回归
            dp[i] = m
        
        return dp[-1]

• 结果

参考：https://blog.youkuaiyun.com/qq_43281792/article/details/85227332?from=groupmessage