Leetcode 1690. 石子游戏 VII (887石子游戏变形，区间dp，前缀和优化）

最新推荐文章于 2025-06-21 02:45:00 发布

原创最新推荐文章于 2025-06-21 02:45:00 发布 · 187 阅读

0 ·

CC 4.0 BY-SA版权

算法专栏收录该内容

3633 篇文章

订阅专栏

本文介绍了一个基于区间动态规划的问题解决方案，通过具体实例展示了如何利用前缀和与动态规划技巧来优化算法性能。针对一个给定的整数数组，通过递推公式计算出使两个玩家得分差值最大化的策略。

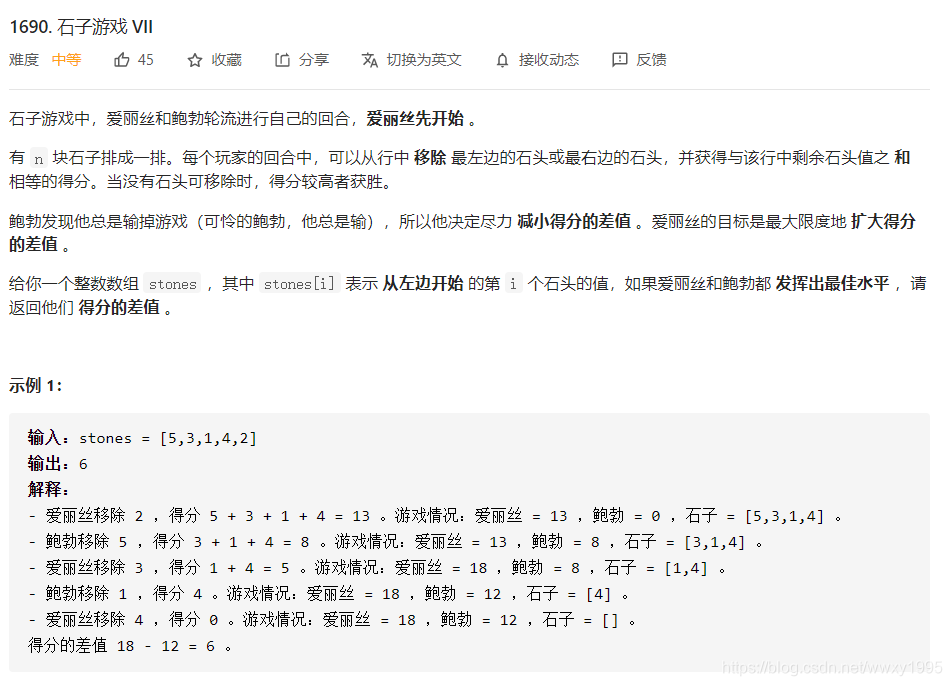
思路和887完全相同，注意一些细节优化即可。

class Solution {
public:
    int stoneGameVII(vector<int>& stones) {
        // f[i][j] 表示区间i到j的当前玩家与对方得分的差
        int n = stones.size();
        vector<int> s(n + 1);
        for(int i = 1; i <=n; i++){
            s[i] = s[i - 1] + stones[i - 1];
        }
        vector<vector<int>> f(n, vector<int>(n));
        for(int k = 2; k <= n; k++){
            for(int i = 0; i + k - 1 < n; i++){
                int j = i + k - 1;
                f[i][j] = max(s[j + 1] - s[i + 1] - f[i + 1][j], s[j] - s[i] - f[i][j - 1]);
            }
        }
        return f[0][n - 1];
    }
};