图像特征检测之直线检测

图像的直线检测

Hough变换
采用参数空间变换的方法，对噪声和不间断直线的检测具有鲁棒性。
核心思想 y=kx+b
可以记为xcosθ+ysinθ=ρ
每一条直线对应一个k，b，参数方程下对应一个点（ρ,θ）
如下图

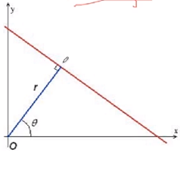
将ρ,θ当做一个新的坐标系，横坐标为θ，纵坐标为ρ，则上面的直线则为当前坐标系中的一个点。

直角坐标系的一个点（x，y），对应极坐标系下的一条正弦曲线ρ=xcosθ+ysinθ = √(x^2+y2 )cos(θ+φ)
同一条直线下的多个点，再极坐标系下比相交于一点

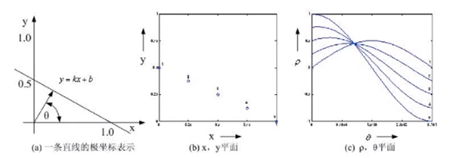
b中的一个点就是在c中的一个余弦曲线，c为极坐标系，a中的一条直线对应c中的一个点，b为a的点集合，c中越多的曲线相交于一点的说明就越有可能是直线的点。

步骤：
1将（ρ,θ）空间量化成许多小格
2根据x-y平面每一个直线点带入θ的量化值，算出各个ρ，将对应格计数累加
3当全部点变换后，对小格进行校验。设置累计阈值T，计数器大于T的小格对应于共线点，其可以用作直线拟合参数。小于T的反映非共线点，丢弃不用。

k,b的值是负无穷到正无穷
而θ是0到2π是个有限的数，坐标系是有限的，ρ最大不会超过原始直线对角线的长度，所以在有界的坐标系中更利于做格子的划分。可用于圆等的检测。类似有投票