求复杂度的时候非常好玩的一个函数

强调下用matlab，因为以前习惯用，想用Python做的可以试试哈！

1. 求解分析T(n)=2(T(n/2))+n^2logn的时间复杂度的时候碰到的，用主方法分析，符合第3种情况，但是我们想求出那个c的取值，最少也得有个范围，是吧？
2. 用代码直接求解，当然，如果你导数公式都记得，那就随意了，直接求导看看结果了：

syms x y
y=(log(x)-1)/(2*log(x));
result=diff(y)
solve(result)

输出结果：

result =
 1/(2*x*log(x)) - (log(x) - 1)/(2*x*log(x)^2)
ans =
 Empty sym: 0-by-1

4. 发现没结果，也就是求导没等于0的玩意儿，分析不好分析，那就直接画图哇！fplot(y,[0,5])，先试试好不？
   
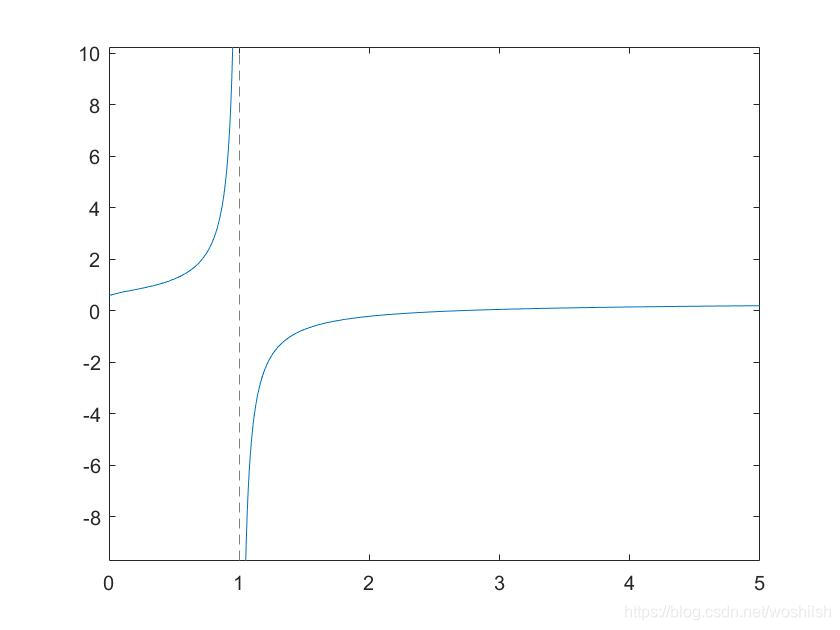
5. 别猴急，看到没？函数原来是这个鸟样，还求什么极值，最值啊，拉倒吧。
6. 在琢磨下我们限定下范围，n>1之后的，不就可以了？
   
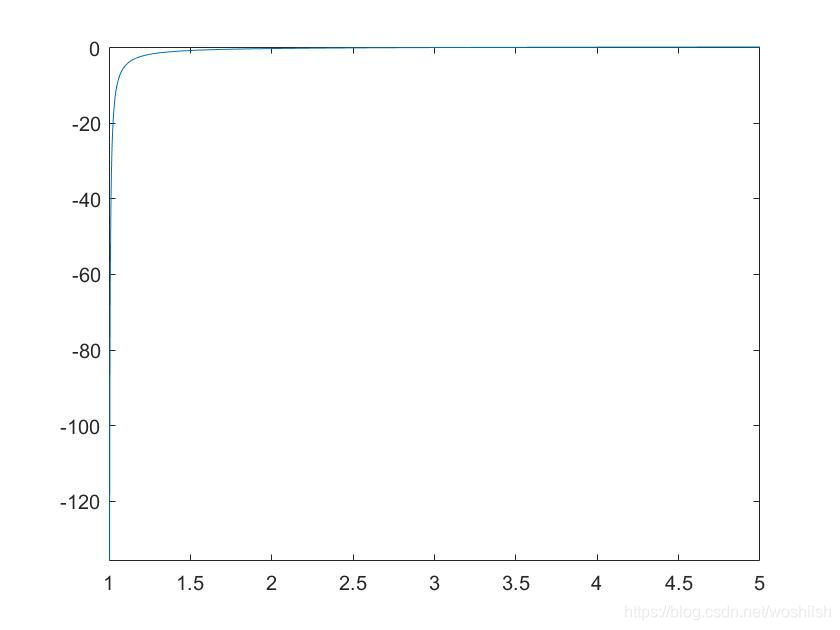
7. 继续琢磨，加大到50000，继续绘制图形
   
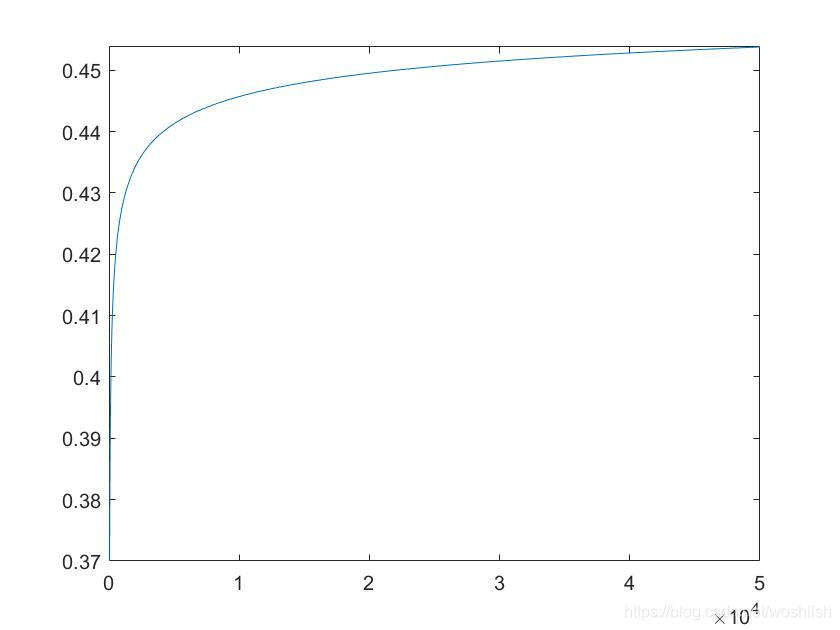
8. 从图中可以看出接近1/2，为哈呢？你取n无穷大，你看看结果是不是1/2=2/4，所以c取3/4应该不成问题，只要c<1就满足条件么。
9. 当然你可以琢磨下，利用代码求，比如：

x0=5
fun=@(x)[(log(x)-1)/(2*log(x))];
[xm,fvalml,maxfval]=fminimax(fun,x0)

这个太粗糙，迭代达不到我们要的精度，需要设计类似于目标优化之类的策略，反正目的达到，不管了，以后有时间琢磨下了。