在将多元线性回归之前先明确几个机器学习中常用的概念。
一、几个级别概念
1.假设函数(Hypothesis)
假设函数:就是预测函数
例如一元线性回归:hθ(x)=θ0+θ1xh_\theta(x) = \theta_0 +\theta_1xhθ(x)=θ0+θ1x
2.损失函数(Lost function)
损失函数:计算的一个样本的误差
例如:lθ(x)=h(xi)−yil_\theta(x) =h(x^i)-y^ilθ(x)=h(xi)−yi
3.代价函数(Cost function)
代价函数:是整个训练集上所有样本误差的平均
例如:Jθ(x)=12m∑i=1m(h(xi)−yi)2J_\theta(x)= \frac{1}{2m} \sum_{i=1}^{m} (h(x^i)-y^i)^2Jθ(x)=2m1∑i=1m(h(xi)−yi)2
4.目标函数(Object function)
目标函数:代价函数 + 正则化项
二、多元线性回归
1.与一元线性回归的区别
如果是单一特征变量,也就是说一个自变量,就是一元线性回归。
如果是多个特征变量,也就是说多个自变量,就是多元线性回归。
例如:hθ(x)=θ0+θ1x1h_\theta(x) = \theta_0 +\theta_1x_1hθ(x)=θ0+θ1x1 只有一个x就是一元的。
hθ(x)=θ0+θ1x1+θ2x2....+θixih_\theta(x) = \theta_0 +\theta_1x_1+\theta_2x_2....+\theta_ix_ihθ(x)=θ0+θ1x1+θ2x2....+θixi 有多个x就是多元的。
2.假设函数(Hypothesis)
假设函数:就是预测函数
例如一元线性回归:hθ(x)=θ0+θ1x1+θ2x2....+θixih_\theta(x) = \theta_0 +\theta_1x_1+\theta_2x_2....+\theta_ix_ihθ(x)=θ0+θ1x1+θ2x2....+θixi
3.损失函数(Lost function)
损失函数:计算的一个样本的误差
例如:lθ(x)=h(xi)−yil_\theta(x) =h(x^i)-y^ilθ(x)=h(xi)−yi
4.代价函数(Cost function)
代价函数:是整个训练集上所有样本误差的平均
例如:J(θ)=12m∑i=1m(hθ(xi)−yi)2J(\theta)= \frac{1}{2m} \sum_{i=1}^{m} (h_\theta(x^i)-y^i)^2J(θ)=2m1∑i=1m(hθ(xi)−yi)2
三、梯度下降
梯度下降只需要记着两个个公式。
θik+1=θik−αJ′(θjk)\theta_{i}^{k+1}=\theta_{i}^{k}-\alpha J{\prime}(\theta_j^k)θik+1=θik−αJ′(θjk)
J′(θjk)=(hθ(xi)−yi)xjiJ{\prime}(\theta_j^k) =(h_\theta(x^i)-y^i)x_j^iJ′(θjk)=(hθ(xi)−yi)xji
推到公式:
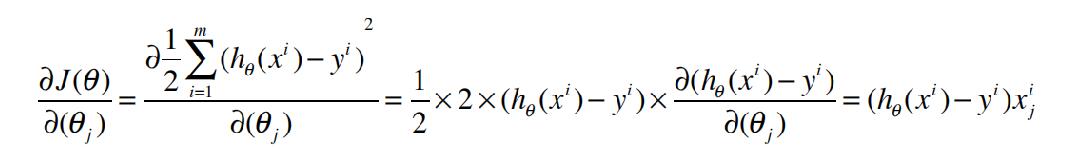








 本文详细解析了机器学习中多元线性回归的基本概念,包括假设函数、损失函数、代价函数和目标函数,并介绍了梯度下降算法的原理与应用。通过对比一元线性回归,阐述了多元线性回归的特点及其数学表达式。
本文详细解析了机器学习中多元线性回归的基本概念,包括假设函数、损失函数、代价函数和目标函数,并介绍了梯度下降算法的原理与应用。通过对比一元线性回归,阐述了多元线性回归的特点及其数学表达式。
















 1626
1626

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








