智能车竞赛舵机抗饱和控制策略

微分冲击： 即使没有积分项（如纯PD控制），当误差发生剧烈变化（如突然检测到一个急弯），PD计算出的指令瞬间要求舵机转到极限位置。舵机以最大速度冲向极限位置的过程可能产生超调或振荡，也可能因为机械冲击影响稳定性。虽然这不严格叫“Windup”，但也是一种需要“抗饱和”处理的瞬态极限情况。

PD控制中的微分冲击问题，是智能车竞赛中影响稳定性的关键点，现在想深入解决纯PD控制下急弯导致的舵机瞬间打满问题。用户可能正在调试一辆高速智能车，在过S弯或直角弯时出现转向抖动甚至冲出赛道的情况。关于微分冲击的应对，需要从三个层面来考虑：首先是D项本身的处理（限幅和滤波），其次是设定值管理（避免突变），最后是系统级优化（路径规划），但可能更需要具体参数调整的技巧。

一是舵机响应速度这个隐藏因素很重要，很多队伍忽略了舵机最大转向角速度的限制。比如计算出的D项指令需要0.1秒转30度，但舵机实际最快只能0.2秒转30度，这时候再完美的算法也会出问题，这个要重点研究。

二是电感车还是摄像头车，两种传感器的噪声特性不同。电感车通常需要更强的低通滤波，而摄像头车在图像处理环节就可以做路径平滑。这个差异会影响D项限幅值的选择，需要补充说明。

三是调试方法论也很关键。一般都是只是知道调Kp/Kd，但其实应该先固定Kp调滤波参数，再调D项限幅，最后微调Kd。这个步骤在实战中能节省大量时间，值得展开。

针对PD控制中微分冲击导致的舵机瞬间饱和问题，以下是具体解决方案和实现细节，可显著提升车辆在急弯突变场景下的稳定性：

---

1. D项输出限幅（核心手段）

原理：限制微分项的最大贡献值，避免误差突变时D项产生过大冲击力。
实现方式：

// PD控制器伪代码
error = target_angle - current_angle;  // 当前路径偏差
P = Kp * error;                        // 比例项

// 计算原始微分项
raw_D = Kd * (error - prev_error) / dt; 

// 对D项限幅（关键！）
if (raw_D > D_MAX) 
    D = D_MAX;
else if (raw_D < -D_MAX) 
    D = -D_MAX;
else 
    D = raw_D;

// 合成输出 + 物理限幅
output = saturate(P + D, -45, 45); // 舵机输出限幅±45°
prev_error = error;

调试技巧：

• D_MAX取值：从舵机最大转向速度反推。
  例：舵机0°→45°需时0.2秒 → 最大角速度 ≈ 225°/s → D_MAX = 225 * Kd（需实测调整）。

• 动态限幅：根据车速调整D_MAX（高速时减小限幅值）。

• 效果：直角弯入弯时舵机转向更平滑，避免“甩尾式”振荡。

---

2. 设定值平滑（预防性策略）

原理：对路径规划输出的目标值（target_angle）进行滤波，避免指令突变。
实现方式：

// 一阶低通滤波（关键参数：滤波系数α）
filtered_target = α * new_target + (1 - α) * prev_target;

// 或使用斜率限制（更简单）
if (new_target - prev_target > MAX_DELTA) 
    filtered_target = prev_target + MAX_DELTA;
else if (new_target - prev_target < -MAX_DELTA) 
    filtered_target = prev_target - MAX_DELTA;
else 
    filtered_target = new_target;

prev_target = filtered_target;

参数选择：

• α取值：0.3~0.7（越小越平滑，但滞后越大）。

• MAX_DELTA：根据舵机性能设定（例：10ms内最大角度变化≤5°）。

• ---

  3. 路径规划优化（系统级解决）

  策略：

• 前瞻距离动态调整：根据车速实时调整前瞻点距离，高速时增加前瞻距离，提前开始转向。

• 路径重采样：在曲率突变处（如直角弯）插入过渡点，强制生成平滑路径。

• 速度规划：在弯心前减速，降低离心力导致的路径跟踪误差。

     软件系统架构图概览

 

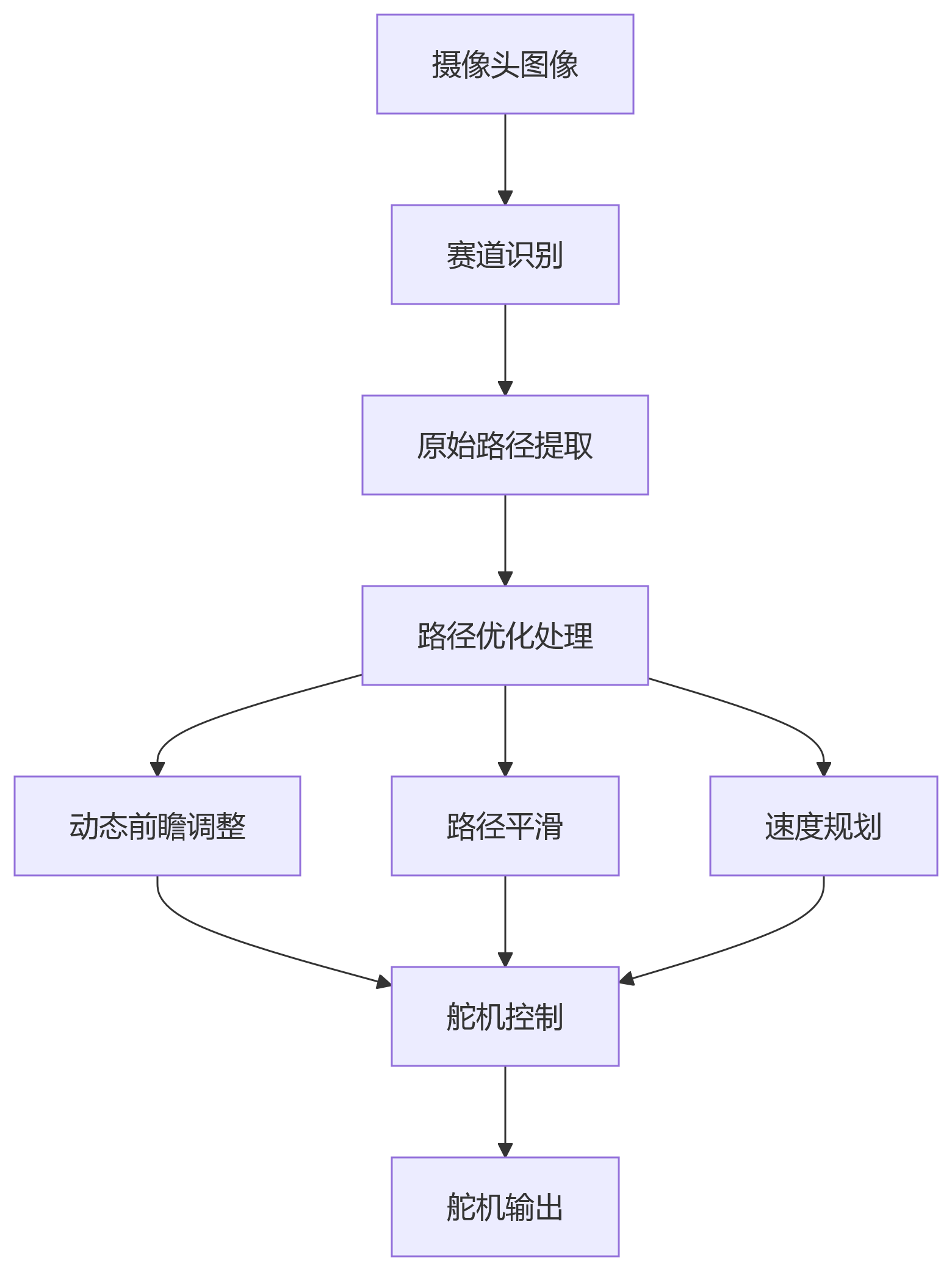
策略一：动态前瞻距离调整

原理说明

在高速行驶时，增大前瞻距离可以让车辆提前感知弯道，避免因突然检测到急弯导致PD控制器输出剧烈变化。前瞻距离根据车速动态调整：

• 低速时：0.3-0.5米（精细控制）

• 高速时：0.8-1.2米（提前转向）

C语言实现

#include <math.h>

// 动态前瞻配置参数
typedef struct {
    float min_distance;   // 最小前瞻距离 (0.3m)
    float max_distance;   // 最大前瞻距离 (1.2m)
    float speed_factor;   // 速度影响因子 (0.1-0.2)
    float curve_factor;   // 弯道影响因子 (0.3-0.5)
} LookaheadConfig;

// 计算动态前瞻距离
float calculate_dynamic_lookahead(float current_speed,