XJTUSE 数据结构与算法第二次作业——任务3和任务4

任务3

1. 题目

众所周知，栈虽然是一个操作受限的线性表，但是其用途却很广泛，栈的数据结构实现非常简单，因此我们只从应用层面熟悉栈。请完成下面三个子任务。

①递归是一种解决很多复杂问题最简单的思想方法，而任何编程语言对递归程序的支持都是通过栈实现的。请利用课堂上讲解的“Hanoi 塔”问题的非递归转化方法完成对递归快速排序的非递归转化。

②算术混合运算表达式的计算。表达式不仅能处理整数，还需要处理小数。表达式中涉及的运算符包括+、-、*、/、^(指数)。表达式可以包含括号（只包含圆括号）嵌套，因此要处理括号匹配失败的情形。

③当我们在使用很多软件时都有类似“undo”功能，比如 Web 浏览器的回退功能、文本编辑器的撤销编辑功能。这些功能都可以使用 Stack 简单实现，但是在现实中浏览器的回退功能也好，编辑器的撤销功能也好，都有一定的数量限制。因此我们需要的不是一个普通的 Stack 数据结构，而是一个空间有限制的 Stack，虽然空间有限，但这样的 Stack 在入栈时从不会溢出，因为它会采用将最久远的记录丢掉的方式让新元素入栈，也就是说总是按照规定的数量要求保持最近的历史操作。比如栈的空间是 5，当 a\b\c\d\e 入栈之后，如果继续让元素 f 入栈，那么栈中的元素将是 b\c\d\e\f。请设计一个满足上面要求的 LeakyStack 数据结构，要求该数据结构的每一个操作的时间复杂度在最坏情形下都必须满足 O(1)。

1. 任务1

1. 算法思路

递归算法通常使用函数调用栈来保存每个递归调用的上下文信息。在非递归实现中，可以使用一个辅助栈来模拟函数调用栈的功能。在每次迭代中，将需要处理的子数组的起始和结束索引压入栈中。

初始化栈并将初始的起始索引和结束索引压入栈，使用Stack<Integer>来表示栈，并初始化一个空栈。然后，我们将初始的起始索引和结束索引压入栈中。

在每次迭代中，从栈中取出起始索引和结束索引，并根据这些索引进行划分。通过调用partition方法来获取枢轴元素的索引，并将其保存为pivotIndex。

检查左子数组和右子数组是否需要进一步划分：在确定了枢轴元素的索引后，需要检查左右子数组是否需要进一步划分。如果左子数组的范围大于1，则将其起始索引和结束索引压入栈中，以便后续处理。同样，如果右子数组的范围大于1，则将其起始索引和结束索引压入栈中。

重复执行步骤3和步骤4，直到栈为空。这样可以保证所有的子数组都得到了正确的划分，并且排序操作会在每个子数组上进行。

1. 主干代码分析

创建一个栈对象stack，并初始化起始索引和结束索引：

1.         Stack<Integer> stack = new Stack<>();
2.         int low = 0;
3.         int high = array.length - 1;
4.         stack.push(low);
5.         stack.push(high);

使用循环迭代处理栈中的元素，在划分操作后，检查左右子数组是否需要进一步划分：

1.         while (!stack.empty()) {
2.             high = stack.pop();
3.             low = stack.pop();
5.             int pivotIndex = partition(array, low, high);
7.             if (pivotIndex - 1 > low) {
8.                 stack.push(low);
9.                 stack.push(pivotIndex - 1);
10.             }
12.             if (pivotIndex + 1 < high) {
13.                 stack.push(pivotIndex + 1);
14.                 stack.push(high);
15.             }
16.         }

1. 测试

测试方法：

1.     public static void main(String[] args) {
2.         int[] array = {7, 2, 1, 6, 8, 5, 3, 4};
3.         System.out.println("原始数组：");
4.         printArray(array);
6.         QuickSortNonRecursive.quickSort(array);
8.         System.out.println("排序后的数组：");
9.         printArray(array);
11.         // 验证排序是否正确
12.         System.out.println("验证排序是否正确：");
13.         if (isSorted(array)) {
14.             System.out.println("数组已正确排序");
15.         } else {
16.             System.out.println("数组排序错误");
17.         }
18.     }
20.     private static void printArray(int[] array) {
21.         for (int num : array) {
22.             System.out.print(num + " ");
23.         }
24.         System.out.println();
25.     }
27.     private static boolean isSorted(int[] array) {
28.         for (int i = 1; i < array.length; i++) {
29.             if (array[i] < array[i - 1]) {
30.                 return false;
31.             }
32.         }
33.         return true;
34.     }

测试结果：

1. 任务2

1. 算法思路

有两种思路来处理算术混合运算表达式的计算。可以直接用两个栈进行中缀表达式的计算，也可以先把中缀表达式转化成后缀表达式再放入栈中计算，两者殊途同归，都是利用了栈只能先入先出的规则，优先计算优先程度高的算式部分，其实也可以理解成一种递归。

我采取了先转化后缀表达式再计算的方式。对于输入要求很低，字符间可以用任意个空格分开，或者根本没有空格，能处理表达式中出现括号不匹配、运算符缺少运算操作数等常见的输入错误。

如何处理括号匹配失败，用一个栈就可以实现，遇到左括号'('时，将其入栈；遇到右括号')'时，进行匹配操作即可。遍历结束后，检查栈是否为空：遍历结束后，我们需要检查栈是否为空。如果栈为空（top为-1），说明所有的左括号都被匹配了，括号匹配成功，返回true。否则，栈中还有未匹配的左括号，括号不匹配，返回false。

1. package homework03;
3. public class BracketMatching {
4.     //利用栈完成括号匹配
5.     static boolean match(char[] exp){
6.         char stack[] = new char[exp.length];
7.         int top=-1;
8.         for (int i=0;i<exp.length;i++){
9.             if (exp[i]=='('){
10.                 stack[++top]='(';//遇到'('则入栈
11.             }
12.             if (exp[i]==')'){
13.                 if (top==-1){
14.                     return false;//栈空说明')'比'('多，不匹配
15.                 }else {
16.                     --top;//栈不空则将栈中的一个'('弹出
17.                 }
18.             }
19.         }
20.         if (top==-1){
21.             return true;//栈空则说明所有括号都被处理掉
22.         }
23.         return false;//否则括号不匹配
24.     }
26. }

如何处理小数和多位数，当扫描到数字时，需要另一个指针j往后继续扫描，当后面是数字时说明是多位数，当扫描到小数点时说明是小数，需要用StringBuilder类型把小数或者多位数拼接，转化成String类型入栈s1.切记把i指针前移。

1.                 if (nifixExp[i] >= '0' && nifixExp[i] <= '9') {
2.                     int j = i;
3.                     StringBuilder number = new StringBuilder();
4.                     while(true){
5.                         if(j >= nifixExp.length){
6.                             break;
7.                         }
8.                         if(nifixExp[j] >= '0' && nifixExp[j] <= '9'){
9.                             number.append(nifixExp[j]);
10.                         } else if (nifixExp[j] == '.') {
11.                             number.append(nifixExp[j]);
12.                         } else{
13.                             break;
14.                         }
15.                         j++;
16.                     }
17.                     i = j - 1;
18.                     s2.push(number.toString());
19.                 } 

1. 主干代码分析

先把中缀表达式转后缀表达式

1初始化两个栈：运算符栈s1和储存中间结果的栈s2；

2从左至右扫描中缀表达式；

3遇到操作数时，将其压s2；

4遇到运算符时，比较其与s1栈顶运算符的优先级：

如果s1为空，或栈顶运算符为左括号“(”，则直接将此运算符入栈；

否则，若优先级比栈顶运算符的高，也将运算符压入s1；

否则，将s1栈顶的运算符弹出并压入到s2中，再次转到(4-1)与s1中新的栈顶运算符相比较；

5遇到括号时：

如果是左括号“(”，则直接压入s1

如果是右括号“)”，则依次弹出s1栈顶的运算符，并压入s2，直到遇到左括号为止，此时将这一对括号丢弃

6重复步骤2至5，直到表达式的最右边

7将s1中剩余的运算符依次弹出并压入s2

8依次弹出s2中的元素并输出，结果的逆序即为中缀表达式对应的后缀表达式

注意点1：栈s1储存Character类型就可以，栈s2必须是Object类型的（需要储存中间结果，有String类型的多位数和小数）。

1.         LStack<Character> s1 = new LStack<>();//存储运算符的栈
2.         LStack<Object> s2 = new LStack<>();//存储中间结果的栈

注意点2：切割成char类型后，对每一个char判断符号是否合法。

1.         for (int i = 0; i < nifix.length(); i++) {
2.             if (!isValid(nifixExp[i])) {
3.                 throw new Exception("输入符号有问题");
4.             }
5.         }

1.     private static boolean isValid(char c) {
2.         return c >= '0' && c <= '9' || c == '+' || c == '-' || c == '*' || c == '/' || c == '^'|| c == ' '|| c == '('|| c == ')'|| c == '.';
3.     }

注意点3：判断括号是否匹配。遇到左括号'('时，将其入栈；遇到右括号')'时，进行匹配操作即可。遍历结束后，检查栈是否为空：遍历结束后，我们需要检查栈是否为空。如果栈为空（top为-1），说明所有的左括号都被匹配了，括号匹配成功，返回true。否则，栈中还有未匹配的左括号，括号不匹配，返回false。上文算法思路中有代码，这里不再展示。

注意点4：当扫描到数字时，需要另一个指针j往后继续不断扫描，当后面是数字时说明是多位数，当扫描到小数点时说明是小数，需要用StringBuilder类型把小数或者多位数拼接，转化成String类型入栈s1.切记把i指针前移。上文算法思路中有代码，这里不再展示。

注意点5：当扫描到五种运算符时，也需要另一个指针j往后继续不断扫描，当后面是空格时j++，扫描到五种运算符、小数点和右括号时报错，其余情况跳出循环。

1.                     int j = i + 1;
2.                     while(true){
3.                         if(j >= nifixExp.length){
4.                             break;
5.                         }
6.                         if(nifixExp[j] == ' '){//继续循环
7.                             j++;
8.                         } else if (nifixExp[j] == '+' ||nifixExp[j] == '-' ||  nifixExp[j] == '*' || nifixExp[j] == '/' ||nifixExp[j] == '^'||nifixExp[j] == '.'||nifixExp[j] == ')') {//报错
9.                             throw new Exception("运算符缺少运算操作数");
10.                         } else{
11.                             break;
12.                         }
13.                     }

注意点6：s2pop的逆序才是后缀表达式。

1.         //依次弹出s2中的元素并输出，
2.         // 结果的逆序即为中缀表达式对应的后缀表达式
3.         Object[] temp = new Object[s2.length()];
4.         for (int i = 0; !s2.isEmpty(); i++) {
5.             temp[i] = s2.pop();
6.         }
7.         StringBuilder stringBuilder = new StringBuilder();
8.         for (int i = temp.length - 1; i >= 0; i--) {
9.             stringBuilder.append(temp[i]);
10.             stringBuilder.append(" ");
11.         }
12.         return stringBuilder.toString();

注意点7：运算符优先级比较函数。

1.     private static boolean comparePriority(char c1, char c2) {//比较运算符优先级
2.         int priority1 = 0, priority2 = 0;
3.         switch (c1) {
4.             case '^' -> priority1 = 3;
5.             case '*' -> priority1 = 2;
6.             case '/' -> priority1 = 2;
7.             case '+' -> priority1 = 1;
8.             case '-' -> priority1 = 1;
9.         }
10.         switch (c2) {
11.             case '^' -> priority2 = 3;
12.             case '*' -> priority2 = 2;
13.             case '/' -> priority2 = 2;
14.             case '+' -> priority2 = 1;
15.             case '-' -> priority2 = 1;
16.         }
17.         return priority1 - priority2 > 0;//c1优先级较高
18.     }

中缀表达式转后缀表达式整体代码如下：

1.     //中缀转后缀
2.     public static String toPostfix(String nifix) throws Exception {
3.         LStack<Character> s1 = new LStack<>();//存储运算符的栈
4.         LStack<Object> s2 = new LStack<>();//存储中间结果的栈
5.         char[] nifixExp = nifix.toCharArray();//将字符串转化为字符数组
6.         for (int i = 0; i < nifix.length(); i++) {
7.             if (!isValid(nifixExp[i])) {
8.                 throw new Exception("输入符号有问题");
9.             }
10.         }
11.         if (!BracketMatching.match(nifixExp)) {
12.             throw new Exception("括号不匹配");
13.         } else {
14.             for (int i = 0; i < nifixExp.length; i++) {//从左到右扫描
15.                 //遇到数字则压入s2，此时s2中的数字是String类型的
16.                 if (nifixExp[i] >= '0' && nifixExp[i] <= '9') {
17.                     int j = i;
18.                     StringBuilder number = new StringBuilder();
19.                     while(true){
20.                         if(j >= nifixExp.length){
21.                             break;
22.                         }
23.                         if(nifixExp[j] >= '0' && nifixExp[j] <= '9'){
24.                             number.append(nifixExp[j]);
25.                         } else if (nifixExp[j] == '.') {
26.                             number.append(nifixExp[j]);
27.                         } else{
28.                             break;
29.                         }
30.                         j++;
31.                     }
32.                     i = j - 1;
33.                     s2.push(number.toString());
34.                 } else if (nifixExp[i] == '(') {//遇到左括号直接压入s1
35.                     s1.push(nifixExp[i]);
36.                 } else if (nifixExp[i] == ')') {
37.                     //遇到右括号“)”，则依次弹出s1栈顶的运算符，并压入s2，直到遇到左括号为止，此时将这一对括号丢弃
38.                     while (!(s1.topValue().equals('('))) {
39.                         s2.push(s1.pop());
40.                     }
41.                     s1.pop();//把左括号也弹出
42.                 } else if (nifixExp[i] != ' ') {
43.                     /*
44.                      * 遇到运算符时，比较其与s1栈顶运算符的优先级：
45.                      * 1) 如果s1为空，或栈顶运算符为左括号“(”，则直接将此运算符入栈；
46.                      * 2) 否则，若优先级比栈顶运算符的高，也将运算符压入s1；
47.                      * 3) 否则，将s1栈顶的运算符弹出并压入到s2中，再次转到(1)与s1中新的栈顶运算符相比较；
48.                      */
49.                     int j = i + 1;
50.                     while(true){
51.                         if(j >= nifixExp.length){
52.                             break;
53.                         }
54.                         if(nifixExp[j] == ' '){//继续循环
55.                             j++;
56.                         } else if (nifixExp[j] == '+' ||nifixExp[j] == '-' ||  nifixExp[j] == '*' || nifixExp[j] == '/' ||nifixExp[j] == '^'||nifixExp[j] == '.'||nifixExp[j] == ')') {//报错
57.                             throw new Exception("运算符缺少运算操作数");
58.                         } else{
59.                             break;
60.                         }
61.                     }
62.                     while (true) {
63.                         if (s1.isEmpty() || s1.topValue() == '('
64.                                 || comparePriority(nifixExp[i], s1.topValue())) {
65.                             s1.push(nifixExp[i]);
66.                             break;
67.                         } else {
68.                             s2.push(s1.pop());
69.                         }
70.                     }
71.                 }
72.             }
73.         }
74.         //把s1中剩余的运算符一次弹出并压入s2
75.         while (!s1.isEmpty()) {
76.             s2.push(s1.pop());
77.         }
78.         //依次弹出s2中的元素并输出，
79.         // 结果的逆序即为中缀表达式对应的后缀表达式
80.         Object[] temp = new Object[s2.length()];
81.         for (int i = 0; !s2.isEmpty(); i++) {
82.             temp[i] = s2.pop();
83.         }
84.         StringBuilder stringBuilder = new StringBuilder();
85.         for (int i = temp.length - 1; i >= 0; i--) {
86.             stringBuilder.append(temp[i]);
87.             stringBuilder.append(" ");
88.         }
89.         return stringBuilder.toString();
90.     }
92.     private static boolean isValid(char c) {
93.         return c >= '0' && c <= '9' || c == '+' || c == '-' || c == '*' || c == '/' || c == '^'|| c == ' '|| c == '('|| c == ')'|| c == '.';
94.     }
96.     private static boolean comparePriority(char c1, char c2) {//比较运算符优先级
97.         int priority1 = 0, priority2 = 0;
98.         switch (c1) {
99.             case '^' -> priority1 = 3;
100.             case '*' -> priority1 = 2;
101.             case '/' -> priority1 = 2;
102.             case '+' -> priority1 = 1;
103.             case '-' -> priority1 = 1;
104.         }
105.         switch (c2) {
106.             case '^' -> priority2 = 3;
107.             case '*' -> priority2 = 2;
108.             case '/' -> priority2 = 2;
109.             case '+' -> priority2 = 1;
110.             case '-' -> priority2 = 1;
111.         }
112.         return priority1 - priority2 > 0;//c1优先级较高
113.     }

后缀表达式的计算机求值

从左至右扫描表达式，遇到数字时，将数字压入堆栈，遇到运算符时，弹出栈顶的两个数，用运算符对它们做相应的计算（次顶元素 和 栈顶元素），并将结果入栈；重复上述过程直到表达式最右端，最后运算得出的值即为表达式的结果。

注意点1：为了区分后缀表达式的多位数，后缀表达式每一个单元word都有一个空格将其隔开。我们需要先根据空格把每一个单元切割开。

1.          String[] expression = expS.split(" ");

注意点2：对expression中的每一个word，如果是数字，将其转为double类型的数字再入栈。

1.             if(isNumeric(word)){
2.                 double number = Double.parseDouble(word);
3.                 stack.push(number);
4.             }

1.     private static boolean isNumeric(String str) {
2.         try {
3.             Double.parseDouble(str);
4.             return true;
5.         } catch (NumberFormatException e) {
6.             return false;
7.         }
8.     }

后缀表达式求值完整代码：

1. //利用栈对后缀表达式求值
2.     static double calculate(String expS) {
3.         String[] expression = expS.split(" ");
4.         LStack<Double> stack = new LStack<>();//存储数字的栈
5.         for (String word : expression) {
6.             if(isNumeric(word)){
7.                 double number = Double.parseDouble(word);
8.                 stack.push(number);
9.             }else{
10.                 //弹出栈顶的两个元素
11.                 double num2 = stack.pop();
12.                 double num1 = stack.pop();
13.                 double temp = -1;;
14.                 switch (word) {
15.                     case "+" -> temp = num1 + num2;
16.                     case "-" -> temp = num1 - num2;
17.                     case "*" -> temp = num1 * num2;
18.                     case "/" -> temp = num1 / num2;
19.                     case "^" -> temp = Math.pow(num1, num2);
20.                 }
21.                 stack.push(temp);//将中间结果压栈
22.             }
23.         }
24.         return stack.topValue();//返回栈顶元素
25.     }
27.     private static boolean isNumeric(String str) {
28.         try {
29.             Double.parseDouble(str);
30.             return true;
31.         } catch (NumberFormatException e) {
32.             return false;
33.         }
34.     }

1. 测试

测试方法：

1.     public static void main(String[] args) throws Exception {
2.         System.out.print("please input your nifix expression: ");
3.         Scanner in = new Scanner(System.in);
4.         String input = in.nextLine();
5.         String postFix = ArithmeticCalculation.toPostfix(input);
6.         double result = calculate(postFix);
7.         System.out.println("the post fix of: " + input + " is " + postFix);
8.         System.out.println("the result of: " + input + " is " + result);
9.     }

测试数据：

包括小数，多位数，五种运算符号，左右括号，很多空格或者无空格等中缀表达式。

包括括号不匹配，输入符号有错，连续多个符号等错误。

2+3*4

(7- 4)      *    2 / (1 + 3)

5.42 * (6   + 2.1 ) - 12

3 + 4 * 2 / (1 - 5) ^ 2

3+((4*2)

45 && 2 + (3*4)

7+  + 2*4

测试结果：

任务3

1. 数据结果设计

为了实现LeakyStack的每个方法都具有O(1)的最坏情况时间复杂度，我们可以使用一个循环数组来实现栈。循环数组是一个固定大小的数组，通过将数组的末尾和开头连接起来，形成一个环形结构。

在LeakyStack中，我们使用一个指针top来表示栈顶元素的位置。该指针随着push和pop操作的进行而不断移动。当执行push操作时，如果栈已满，我们会通过丢弃最早的元素来腾出空间，让新元素入栈。具体来说，当栈已满时，我们将top指针向前移动一位，并将新元素放在这个位置，从而覆盖掉最早的元素。这样，栈的容量始终保持固定，且新元素的入栈操作的时间复杂度为O(1)。

这种设计使得栈的操作时间与栈的容量无关，始终保持恒定的时间复杂度。无论是执行push、pop、topValue还是判断栈是否为空或已满，都只需要对指针进行简单的移动或比较操作，而不需要对整个数组进行移动或复制。

LeakySteak中，有int类型的maxSize表示基于数组实现的栈能够容纳的最大栈元素个数；有int类型的top表示一个指针，指向栈顶位置，初始是-1；T[]类型的listArray定义泛型类型的数组引用；int类型的number表示栈中数据的数量。

1.     // 数组实现, 一个循环数组，栈顶和栈底位置相差1，像队列
2.     private int maxSize;             //基于数组实现的栈能够容纳的最大栈元素个数。
3.     private int top;                 // 指向栈顶位置。
4.     private T[] listArray;           // 定义泛型类型的数组引用。
5.     private int number;              // 栈中数据的数量
7.     public LeakyStack(int maxSize) {
8.         this.maxSize = maxSize;
9.         this.top = -1;
10.         this.listArray = (T[]) new Object[maxSize];
11.     }

Push入栈：

指针先后移一位，如果越界则说明栈已满，指针指向0处，number--便于与下面的number++代码抵消；number++；it填充到栈顶。

1.     @Override
2.     public void push(T it) {
3.         top++;
4.         if(top == maxSize){
5.             top -= maxSize;
6.             number--;
7.         }
8.         number++;
9.         listArray[top] = it;
10.     }

Pop出栈：

当栈非空时操作；先储存出栈的数据；将其置为null，top--，判断是否越界并处理；

number--；返回出栈数据。

1.     @Override
2.     public T pop() {
3.         if(!isEmpty()){
4.             T temp = listArray[top];
5.             listArray[top] = null;
6.             top--;
7.             if(top == -1){
8.                 top += maxSize;
9.             }
10.             number--;
11.             return temp;
12.         }
13.         return null;
14.     }

其他操作相对简单不在此处进行分析。

1.     @Override
2.     public void clear() {
3.         top = -1;
4.         number =  0;
5.     }
7.     @Override
8.     public T topValue() {
9.         return listArray[top];
10.     }
12.     @Override
13.     public int length() {
14.         return number;
15.     }
17.     @Override
18.     public boolean isEmpty() {
19.         return number == 0;
20.     }
22.     @Override
23.     public boolean isFull() {
24.         return number == maxSize;
25.     }

1. 时间复杂度分析

clear(): 时间复杂度为O(1)。该方法只是简单地将栈顶指针和元素数量重置为0，没有遍历操作。

push(T it): 时间复杂度为O(1)。该方法只是将新元素入栈，并更新栈顶指针和元素数量。

pop(): 时间复杂度为O(1)。该方法只是将栈顶元素弹出，并更新栈顶指针和元素数量。

topValue(): 时间复杂度为O(1)。该方法只是返回栈顶元素，并不改变栈的结构。

length(): 时间复杂度为O(1)。该方法只是返回当前栈中元素的数量，由于维护了一个变量来记录元素数量，所以可以直接返回。

isEmpty(): 时间复杂度为O(1)。该方法只是判断栈是否为空，通过检查元素数量是否为0来确定。

isFull(): 时间复杂度为O(1)。该方法只是判断栈是否已满，通过检查元素数量是否达到最大容量来确定。

LeakyStack的每个方法都具有O(1)的最坏情况时间复杂度。这是因为使用了一个循环数组来实现栈，并且在入栈时通过丢弃最早的元素来保持固定的容量，而无需对整个数组进行移动或复制操作。这种设计使得栈的操作时间与栈的容量无关，始终保持恒定的时间复杂度。

1. 测试

1.     public static void main(String[] args) {
2.         LeakyStack<String> stack = new LeakyStack<>(5);
4.         stack.push("a");
5.         stack.push("b");
6.         stack.push("c");
7.         stack.push("d");
8.         stack.push("e");
10.         System.out.println("栈长度：" + stack.length());  // 输出：栈长度：5
11.         System.out.println("栈顶元素：" + stack.topValue());  // 输出：栈顶元素：e
13.         stack.push("f");
14.         System.out.println("栈长度：" + stack.length());  // 输出：栈长度：5
15.         System.out.println("栈顶元素：" + stack.topValue());  // 输出：栈顶元素：f
17.         String poppedValue = stack.pop();
18.         System.out.println("弹出的元素：" + poppedValue);  // 输出：弹出的元素：f
19.         System.out.println("栈长度：" + stack.length());  // 输出：栈长度：4
20.         System.out.println("栈顶元素：" + stack.topValue());  // 输出：栈顶元素：e
22.         stack.clear();
23.         System.out.println("栈长度：" + stack.length());  // 输出：栈长度：0
24.         System.out.println("栈是否为空：" + stack.isEmpty());  // 输出：栈是否为空：true
25.     }

结果：

1. 总结和收获

任务1学到了递归问题如何转化成非递归问题。

任务2复习了字符字符串相关操作，深入理解了栈的应用，更加理解递归，也学到了中缀表达式和后缀表达式。

任务3自己写了一个栈的一个具体应用的数据机构，这说明针对具体的问题，要用更加具体的切合实际的数据结构，要定制数据结构。

任务4

1. 题目

使用自定义的队列数据结构实现对某一个数据序列的排序(采用基数排序)，其中对待排序数据有如下的要求:

①当数据序列是整数类型的数据的时候，数据序列中每个数据的位数不要求等宽，比如: 1、21、12、322、44、123、2312、765、56

②当数据序列是字符串类型的数据的时候，数据序列中每个字符串都是等宽的，比如:

"abc","bde","fad","abd","bef","fdd","abe"

注：radixsort1.txt 和 radixsort2.txt 是为上面两个数据序列提供的测试数据。

1. 数据设计

需要做一个队列Queue，链式队列最容易实现，列表只需要单链表就可以，也不需要头尾哨兵节点,有两个指针分别指向队头和队尾，有一个int类型的size储存列表的节点数量。当列表为空的时候两个指针指向null。

1. public class MyQueue<T> implements Queue<T>{
3.     private static class Node<T> {
4.         T value;
5.         Node<T> next;
7.         public Node(T value, Node<T> next) {
8.             this.value = value;
9.             this.next = next;
10.         }
11.     }
13.     private Node<T> front;
14.     private Node<T> rear;
15.     private int size;
17.     public MyQueue() {
18.         this.front = null;
19.         this.rear = null;
20.         this.size = 0;
21.     }
22. }

列表实现起来非常简单，队尾添加元素的add方法，当列表为空的时候将头尾指针指向新加入的节点，当列表非空的时候将尾指针指向新加的节点即可。

1.     @Override
2.     public boolean add(T data) {
3.         if (isEmpty()) {
4.             Node<T> added = new Node<>(data, null);
5.             front = added;
6.             rear = added;
7.             return true;
8.         } else {
9.             Node<T> added = new Node<>(data, null);
10.             rear.next = added;
11.             rear = added;
12.             return true;
13.         }
14.     }

队头删除元素的poll方法，当列表非空的时候将头指针向前指一位，移除后，检查下列表是否为空，如果是将尾指针也置空。

1.     @Override
2.     public T poll() {
3.         if (isEmpty()) {
4.             return null;
5.         }
6.         Node<T> temp = front;
7.         front = front.next;
8.         if (front == null) {
9.             // 如果队列为空，更新rear为null
10.             rear = null;
11.         }
12.         return temp.value;
13.     }

1. 算法设计和主干代码分析

对于数字和等长字符串，采用最低位优先法排序最快速。LSD基数排序算法从最低有效位开始，通过将元素按照当前位的值分配到不同的队列中，然后按照队列的顺序将元素收集回原始数组。然后，它继续处理下一位，重复这个过程，直到处理完最高有效位为止。通过这样的迭代，元素将按照每个位的顺序进行排序，最终实现整体的排序。

LSD（Least Significant Digit）基数排序算法的时间复杂度取决于输入数据的位数和数据范围。假设输入数据的长度为n，位数为d，数据范围为k。

时间复杂度：O(d * (n + k))

1.外层循环迭代d次，每次迭代处理一个位数。

2.在每个位数上，需要对n个元素进行分配到k个桶的操作，这需要线性时间，即O(n)。

3.需要从k个桶中收集元素放回原始数组，也需要线性时间，即O(n)。

4.每个位数上的操作总共需要O(n + k)的时间。

对整数排序的LSD算法：

1.用一个List<MyQueue<Integer>> queues创建10个MyQueue队列，用于存储待排序的整数，每个队列代表一个数字（0到9）。

1.         //十个队列，queues.get(2);表示拿出第三个队列
2.         List<MyQueue<Integer>> queues = new ArrayList<>();
3.         //最开始建10个队列
4.         for (int i = 0; i < 10; i++) {
5.             MyQueue<Integer> queue = new MyQueue<>();
6.             queues.add(queue);
7.         }

2.确定数组中最大整数的位数，即digits。将整个数组寻找最大的数，再得到最高位数。

1.     private static int getNumDigits(int[] num) {//获得最大的数的位数
2.         int max = num[0];//最大的数
3.         int digits = 0;//位数
4.         for (int i = 0; i < num.length; i++) {
5.             if (num[i] > max) max = num[i];
6.         }
7.         while (max / 10 != 0) {
8.             digits++;
9.             max = max / 10;
10.         }
11.         if (max % 10 != 0) {
12.             digits++;
13.         }
14.         return digits;
15.     }

3.初始化mode为1，用一个while循环，从最低位开始排序，直到最高位。

1.         int mode = 1;
2.         while (digits != 0) {
3.             //入队
4.             //出队
5.             digits--;//位上移
6.             mode = mode * 10;
7.         }

4.将数组中的元素根据当前位的值入队到相应的队列中。通过 (value / mode) % 10 可以获取当前位的值。

1.             //入队
2.             for (int value : num) {
3.                 queues.get((value / mode) % 10).add(value);
4.             }

5.从0到9遍历队列，依次将队列中的元素出队并放回原始数组中。

1.             //出队,k表示数组中的
2.             int k = 0;
3.             //j表示第几个队列
4.             for(int j = 0; j < 10; j++){
5.                 while(!queues.get(j).isEmpty()){
6.                     num[k] = queues.get(j).poll();
7.                     k++;
8.                 }
9.             }

对字符串排序的LSD算法：

1.用一个List<MyQueue<String>> queues创建52个MyQueue队列，用于存储待排序的大小写字母，每个队列代表一个字母。

1.         //52个队列，queues.get(2);表示拿出第三个队列
2.         List<MyQueue<String>> queues = new ArrayList<>();
3.         //最开始建52个队列
4.         for (int i = 0; i < 52; i++) {
5.             MyQueue<String> queue = new MyQueue<>();
6.             queues.add(queue);
7.         }

2.确定数组中最高位数，即digits。因为本题目处理相同位数的字母，只需要得到str[0]的长度即可。

3.初始化mode为1，用一个while循环，从最低位开始排序，直到最高位。跟整数LSD一致，不再给出代码。

4.根据当前判断的位数将数组中的元素的值入队到相应的队列中。

1.             //入队
2.             for (String letter : str) {
3.                 queues.get(getSize(getCharByDigits(digits,letter))).add(letter);
4.             }

1.     //根据几位数返回char
2.     private static char getCharByDigits(int digit, String string){
3.         char[] charArray = string.toCharArray();
4.         return charArray[digit - 1];
5.     }

1.     private static int getSize(char letter){
2.         if('a' <= letter && letter <= 'z'){
3.             //a返回的是0
4.             return letter - 97;
5.         } else if ('A' <= letter && letter <= 'Z') {
6.             //A返回的是26
7.             return letter - 65 + 26;
8.         }
9.         return -1;
10.     }

5.遍历队列，依次将队列中的元素出队并放回原始数组中。代码与整数LSD一致，在这里不再展示。

1. 测试代码

我希望看到排序前后的数据，希望得到运行时间，希望将数据50个一组存入新的output文件，当然必不可少的是读取文件中的数据。

读取文件中的数据，两个方法分别是readNumbersFromFile和readStringsFromFile。

1.     private static int[] readNumbersFromFile(String filePath) {
2.         int[] numbers = null;
3.         try {
4.             File file = new File(filePath);
5.             Scanner scanner = new Scanner(file);
6.             //计算文件中有多少个数
7.             int count = 0;
8.             while (scanner.hasNext()) {
9.                 if (scanner.hasNextInt()) {
10.                     scanner.nextInt();
11.                     count++;
12.                 } else {
13.                     scanner.next();
14.                 }
15.             }
16.             scanner.close();
17.             //把数字填入数组
18.             numbers = new int[count];
19.             scanner = new Scanner(file);
20.             int index = 0;
21.             while (scanner.hasNext()) {
22.                 if (scanner.hasNextInt()) {
23.                     numbers[index] = scanner.nextInt();
24.                     index++;
25.                 } else {
26.                     scanner.next();
27.                 }
28.             }
29.             scanner.close();
30.         } catch (FileNotFoundException e) {
31.             e.printStackTrace();
32.         }
33.         return numbers;
34.     }
36.     private static String[] readStringsFromFile(String filePath) {
37.         String[] strings = null;
38.         try {
39.             File file = new File(filePath);
40.             Scanner scanner = new Scanner(file);
41.             // 计算文件中有多少个字符串
42.             int count = 0;
43.             while (scanner.hasNext()) {
44.                 if (scanner.hasNext()) {
45.                     scanner.next();
46.                     count++;
47.                 } else {
48.                     scanner.next();
49.                 }
50.             }
51.             scanner.close();
52.             // 把字符串填入数组
53.             strings = new String[count];
54.             scanner = new Scanner(file);
55.             int index = 0;
56.             while (scanner.hasNext()) {
57.                 if (scanner.hasNext()) {
58.                     strings[index] = scanner.next();
59.                     index++;
60.                 } else {
61.                     scanner.next();
62.                 }
63.             }
64.             scanner.close();
65.         } catch (FileNotFoundException e) {
66.             e.printStackTrace();
67.         }
68.         return strings;
69.     }

将排序好的数据50个一行存入新的output文件。

1.     private static void writeNumbersToFile(int[] numbers, String filePath) {
2.         try {
3.             PrintWriter writer = new PrintWriter(filePath);
4.             int count = 0;
5.             for (int number : numbers) {
6.                 writer.print(number + " ");
7.                 count++;
8.                 if (count % 50 == 0) {
9.                     writer.println();
10.                 }
11.             }
12.             writer.close();
13.         } catch (FileNotFoundException e) {
14.             e.printStackTrace();
15.         }
16.     }
18.     private static void writeStringsToFile(String[] strings, String filePath) {
19.         try {
20.             PrintWriter writer = new PrintWriter(filePath);
21.             int count = 0;
22.             for (String str : strings) {
23.                 writer.print(str + " ");
24.                 count++;
25.                 if (count % 50 == 0) {
26.                     writer.println();
27.                 }
28.             }
29.             writer.close();
30.         } catch (FileNotFoundException e) {
31.             e.printStackTrace();
32.         }
33.     }

1. 运行结果展示
    

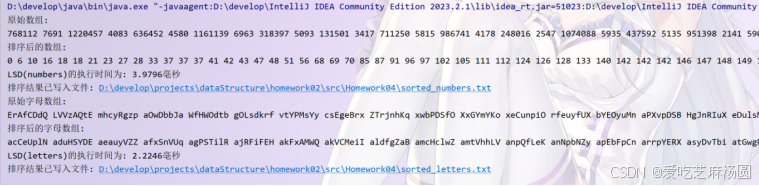
1. 总结和收获

学习了基数排序LSD算法，也进一步学习了文件的读取，写出，整体收获很大。

附录：

1. 任务3

1. QuickSortNonRecursive：

1. package homework03;
3. import java.util.Stack;
5. public class QuickSortNonRecursive {
6.     public static void quickSort(int[] array) {
7.         Stack<Integer> stack = new Stack<>();
8.         int low = 0;
9.         int high = array.length - 1;
10.         stack.push(low);
11.         stack.push(high);
13.         while (!stack.empty()) {
14.             high = stack.pop();
15.             low = stack.pop();
17.             int pivotIndex = partition(array, low, high);
19.             if (pivotIndex - 1 > low) {
20.                 stack.push(low);
21.                 stack.push(pivotIndex - 1);
22.             }
24.             if (pivotIndex + 1 < high) {
25.                 stack.push(pivotIndex + 1);
26.                 stack.push(high);
27.             }
28.         }
29.     }
31.     private static int partition(int[] array, int low, int high) {
32.         int pivot = array[high];
33.         int i = low - 1;
35.         for (int j = low; j < high; j++) {
36.             if (array[j] < pivot) {
37.                 i++;
38.                 swap(array, i, j);
39.             }
40.         }
42.         swap(array, i + 1, high);
43.         return i + 1;
44.     }
46.     private static void swap(int[] array, int i, int j) {
47.         int temp = array[i];
48.         array[i] = array[j];
49.         array[j] = temp;
50.     }
52.     public static void main(String[] args) {
53.         int[] array = {7, 2, 1, 6, 8, 5, 3, 4};
54.         System.out.println("原始数组：");
55.         printArray(array);
57.         QuickSortNonRecursive.quickSort(array);
59.         System.out.println("排序后的数组：");
60.         printArray(array);
62.         // 验证排序是否正确
63.         System.out.println("验证排序是否正确：");
64.         if (isSorted(array)) {
65.             System.out.println("数组已正确排序");
66.         } else {
67.             System.out.println("数组排序错误");
68.         }
69.     }
71.     private static void printArray(int[] array) {
72.         for (int num : array) {
73.             System.out.print(num + " ");
74.         }
75.         System.out.println();
76.     }
78.     private static boolean isSorted(int[] array) {
79.         for (int i = 1; i < array.length; i++) {
80.             if (array[i] < array[i - 1]) {
81.                 return false;
82.             }
83.         }
84.         return true;
85.     }
86. }

1. 老师提供的Stack接口不再展示：
2. 老师提供的LStack不在展示：
3. BracketMatching：

1. package homework03;
3. public class BracketMatching {
4.     //利用栈完成括号匹配
5.     static boolean match(char[] exp){
6.         char stack[] = new char[exp.length];
7.         int top=-1;
8.         for (int i=0;i<exp.length;i++){
9.             if (exp[i]=='('){
10.                 stack[++top]='(';//遇到'('则入栈
11.             }
12.             if (exp[i]==')'){
13.                 if (top==-1){
14.                     return false;//栈空说明')'比'('多，不匹配
15.                 }else {
16.                     --top;//栈不空则将栈中的一个'('弹出
17.                 }
18.             }
19.         }
20.         if (top==-1){
21.             return true;//栈空则说明所有括号都被处理掉
22.         }
23.         return false;//否则括号不匹配
24.     }
26. }

1. ArithmeticCalculation：

1. package homework03;
3. import java.util.Scanner;
5. /**
6.  * post fix：后缀表达式。
7.  * nifix：中缀表达式。
8.  */
9. public class ArithmeticCalculation {
10.     //中缀转后缀
11.     public static String toPostfix(String nifix) throws Exception {
12.         LStack<Character> s1 = new LStack<>();//存储运算符的栈
13.         LStack<Object> s2 = new LStack<>();//存储中间结果的栈
14.         char[] nifixExp = nifix.toCharArray();//将字符串转化为字符数组
15.         for (int i = 0; i < nifix.length(); i++) {
16.             if (!isValid(nifixExp[i])) {
17.                 throw new Exception("输入符号有问题");
18.             }
19.         }
20.         if (!BracketMatching.match(nifixExp)) {
21.             throw new Exception("括号不匹配");
22.         } else {
23.             for (int i = 0; i < nifixExp.length; i++) {//从左到右扫描
24.                 //遇到数字则压入s2，此时s2中的数字是String类型的
25.                 if (nifixExp[i] >= '0' && nifixExp[i] <= '9') {
26.                     int j = i;
27.                     StringBuilder number = new StringBuilder();
28.                     while(true){
29.                         if(j >= nifixExp.length){
30.                             break;
31.                         }
32.                         if(nifixExp[j] >= '0' && nifixExp[j] <= '9'){
33.                             number.append(nifixExp[j]);
34.                         } else if (nifixExp[j] == '.') {
35.                             number.append(nifixExp[j]);
36.                         } else{
37.                             break;
38.                         }
39.                         j++;
40.                     }
41.                     i = j - 1;
42.                     s2.push(number.toString());
43.                 } else if (nifixExp[i] == '(') {//遇到左括号直接压入s1
44.                     s1.push(nifixExp[i]);
45.                 } else if (nifixExp[i] == ')') {
46.                     //遇到右括号“)”，则依次弹出s1栈顶的运算符，并压入s2，直到遇到左括号为止，此时将这一对括号丢弃
47.                     while (!(s1.topValue().equals('('))) {
48.                         s2.push(s1.pop());
49.                     }
50.                     s1.pop();//把左括号也弹出
51.                 } else if (nifixExp[i] != ' ') {
52.                     /*
53.                      * 遇到运算符时，比较其与s1栈顶运算符的优先级：
54.                      * 1) 如果s1为空，或栈顶运算符为左括号“(”，则直接将此运算符入栈；
55.                      * 2) 否则，若优先级比栈顶运算符的高，也将运算符压入s1；
56.                      * 3) 否则，将s1栈顶的运算符弹出并压入到s2中，再次转到(1)与s1中新的栈顶运算符相比较；
57.                      */
58.                     int j = i + 1;
59.                     while(true){
60.                         if(j >= nifixExp.length){
61.                             break;
62.                         }
63.                         if(nifixExp[j] == ' '){//继续循环
64.                             j++;
65.                         } else if (nifixExp[j] == '+' ||nifixExp[j] == '-' ||  nifixExp[j] == '*' || nifixExp[j] == '/' ||nifixExp[j] == '^'||nifixExp[j] == '.'||nifixExp[j] == ')') {//报错
66.                             throw new Exception("运算符缺少运算操作数");
67.                         } else{
68.                             break;
69.                         }
70.                     }
71.                     while (true) {
72.                         if (s1.isEmpty() || s1.topValue() == '('
73.                                 || comparePriority(nifixExp[i], s1.topValue())) {
74.                             s1.push(nifixExp[i]);
75.                             break;
76.                         } else {
77.                             s2.push(s1.pop());
78.                         }
79.                     }
80.                 }
81.             }
82.         }
83.         //把s1中剩余的运算符一次弹出并压入s2
84.         while (!s1.isEmpty()) {
85.             s2.push(s1.pop());
86.         }
87.         //依次弹出s2中的元素并输出，
88.         // 结果的逆序即为中缀表达式对应的后缀表达式
89.         Object[] temp = new Object[s2.length()];
90.         for (int i = 0; !s2.isEmpty(); i++) {
91.             temp[i] = s2.pop();
92.         }
93.         StringBuilder stringBuilder = new StringBuilder();
94.         for (int i = temp.length - 1; i >= 0; i--) {
95.             stringBuilder.append(temp[i]);
96.             stringBuilder.append(" ");
97.         }
98.         return stringBuilder.toString();
99.     }
101.     private static boolean isValid(char c) {
102.         return c >= '0' && c <= '9' || c == '+' || c == '-' || c == '*' || c == '/' || c == '^'|| c == ' '|| c == '('|| c == ')'|| c == '.';
103.     }
105.     private static boolean comparePriority(char c1, char c2) {//比较运算符优先级
106.         int priority1 = 0, priority2 = 0;
107.         switch (c1) {
108.             case '^' -> priority1 = 3;
109.             case '*' -> priority1 = 2;
110.             case '/' -> priority1 = 2;
111.             case '+' -> priority1 = 1;
112.             case '-' -> priority1 = 1;
113.         }
114.         switch (c2) {
115.             case '^' -> priority2 = 3;
116.             case '*' -> priority2 = 2;
117.             case '/' -> priority2 = 2;
118.             case '+' -> priority2 = 1;
119.             case '-' -> priority2 = 1;
120.         }
121.         return priority1 - priority2 > 0;//c1优先级较高
122.     }
124.     //利用栈对后缀表达式求值
125.     static double calculate(String expS) {
126.         String[] expression = expS.split(" ");
127.         LStack<Double> stack = new LStack<>();//存储数字的栈
128.         for (String word : expression) {
129.             if(isNumeric(word)){
130.                 double number = Double.parseDouble(word);
131.                 stack.push(number);
132.             }else{
133.                 //弹出栈顶的两个元素
134.                 double num2 = stack.pop();
135.                 double num1 = stack.pop();
136.                 double temp = -1;;
137.                 switch (word) {
138.                     case "+":
139.                         temp = num1 + num2;
140.                         break;
141.                     case "-":
142.                         temp = num1 - num2;
143.                         break;
144.                     case "*":
145.                         temp = num1 * num2;
146.                         break;
147.                     case "/":
148.                         temp = num1 / num2;
149.                         break;
150.                     case "^":
151.                         temp = Math.pow(num1,num2);
152.                         break;
153.                 }
154.                 stack.push(temp);//将中间结果压栈
155.             }
156.         }
157.         return stack.topValue();//返回栈顶元素
158.     }
160.     private static boolean isNumeric(String str) {
161.         try {
162.             Double.parseDouble(str);
163.             return true;
164.         } catch (NumberFormatException e) {
165.             return false;
166.         }
167.     }
169.     public static void main(String[] args) throws Exception {
170.         System.out.print("please input your nifix expression: ");
171.         Scanner in = new Scanner(System.in);
172.         String input = in.nextLine();
173.         String postFix = ArithmeticCalculation.toPostfix(input);
174.         double result = calculate(postFix);
175.         System.out.println("the post fix of: " + input + " is " + postFix);
176.         System.out.println("the result of: " + input + " is " + result);
177.     }
178. }

1. LeakyStack：

1. package homework03;
3. /**
4.  * 当我们在使用很多软件时都有类似“undo”功能，比如 Web 浏览器的回退功能、文本编辑器
5.  * 的撤销编辑功能。这些功能都可以使用 Stack 简单实现，但是在现实中浏览器的回退功能也好，
6.  * 编辑器的撤销功能也好，都有一定的数量限制。因此我们需要的不是一个普通的 Stack 数据结构，
7.  * 而是一个空间有限制的 Stack，虽然空间有限，但这样的 Stack 在入栈时从不会溢出，因为它会
8.  * 采用将最久远的记录丢掉的方式让新元素入栈，也就是说总是按照规定的数量要求保持最近的历
9.  * 史操作。比如栈的空间是 5，当 a\b\c\d\e 入栈之后，如果继续让元素 f 入栈，那么栈中的元素
10.  * 将是 b\c\d\e\f。请设计一个满足上面要求的 LeakyStack 数据结构，要求该数据结构的每一个操
11.  * 作的时间复杂度在最坏情形下都必须满足 O(1)。
12.  */
13. public class LeakyStack<T> implements Stack<T> {
14.     // 数组实现, 一个循环数组，栈顶和栈底位置相差1，像队列
15.     private int maxSize;             //基于数组实现的栈能够容纳的最大栈元素个数。
16.     private int top;                 // 指向栈顶位置。
17.     private T[] listArray;           // 定义泛型类型的数组引用。
18.     private int number;              // 栈中数据的数量
20.     public LeakyStack(int maxSize) {
21.         this.maxSize = maxSize;
22.         this.top = -1;
23.         this.listArray = (T[]) new Object[maxSize];
24.     }
26.     @Override
27.     public void clear() {
28.         top = -1;
29.         number =  0;
30.     }
32.     @Override
33.     public void push(T it) {
34.         top++;
35.         if(top == maxSize){
36.             top -= maxSize;
37.             number--;
38.         }
39.         number++;
40.         listArray[top] = it;
41.     }
43.     @Override
44.     public T pop() {
45.         if(!isEmpty()){
46.             T temp = listArray[top];
47.             listArray[top] = null;
48.             top--;
49.             if(top == -1){
50.                 top += maxSize;
51.             }
52.             number--;
53.             return temp;
54.         }
55.         return null;
56.     }
58.     @Override
59.     public T topValue() {
60.         return listArray[top];
61.     }
63.     @Override
64.     public int length() {
65.         return number;
66.     }
68.     @Override
69.     public boolean isEmpty() {
70.         return number == 0;
71.     }
73.     @Override
74.     public boolean isFull() {
75.         return number == maxSize;
76.     }
79.     public static void main(String[] args) {
80.         LeakyStack<String> stack = new LeakyStack<>(5);
82.         stack.push("a");
83.         stack.push("b");
84.         stack.push("c");
85.         stack.push("d");
86.         stack.push("e");
88.         System.out.println("栈长度：" + stack.length());  // 输出：栈长度：5
89.         System.out.println("栈顶元素：" + stack.topValue());  // 输出：栈顶元素：e
91.         stack.push("f");
92.         System.out.println("栈长度：" + stack.length());  // 输出：栈长度：5
93.         System.out.println("栈顶元素：" + stack.topValue());  // 输出：栈顶元素：f
95.         String poppedValue = stack.pop();
96.         System.out.println("弹出的元素：" + poppedValue);  // 输出：弹出的元素：f
97.         System.out.println("栈长度：" + stack.length());  // 输出：栈长度：4
98.         System.out.println("栈顶元素：" + stack.topValue());  // 输出：栈顶元素：e
100.         stack.clear();
101.         System.out.println("栈长度：" + stack.length());  // 输出：栈长度：0
102.         System.out.println("栈是否为空：" + stack.isEmpty());  // 输出：栈是否为空：true
103.     }
106. }

1. 任务4

1. MyQueue：

1. package Homework04;
3. /**
4.  * 链式队列:
5.  * 单链表,带头尾指针,没有头尾哨兵
6.  */
7. public class MyQueue<T> implements Queue<T>{
9.     private static class Node<T> {
10.         T value;
11.         Node<T> next;
13.         public Node(T value, Node<T> next) {
14.             this.value = value;
15.             this.next = next;
16.         }
17.     }
19.     private Node<T> front;
20.     private Node<T> rear;
21.     private int size;
23.     public MyQueue() {
24.         this.front = null;
25.         this.rear = null;
26.         this.size = 0;
27.     }
29.     @Override
30.     public int size() {
31.         return size;
32.     }
34.     @Override
35.     public boolean isEmpty() {
36.         return front==null&&rear==null;
37.     }
39.     @Override
40.     public boolean add(T data) {
41.         if (isEmpty()) {
42.             Node<T> added = new Node<>(data, null);
43.             front = added;
44.             rear = added;
45.             return true;
46.         } else {
47.             Node<T> added = new Node<>(data, null);
48.             rear.next = added;
49.             rear = added;
50.             return true;
51.         }
52.     }
55.     @Override
56.     public T peek() {
57.         if(isEmpty()){
58.             return null;
59.         }
60.         return front.value;
61.     }
64.     @Override
65.     public T poll() {
66.         if (isEmpty()) {
67.             return null;
68.         }
69.         Node<T> temp = front;
70.         front = front.next;
71.         if (front == null) {
72.             // 如果队列为空，更新rear为null
73.             rear = null;
74.         }
75.         return temp.value;
76.     }
78.     @Override
79.     public void clearQueue() {
80.         front = null;
81.         rear = null;
82.     }
83. }

1. RadixSort：

1. package Homework04;
3. import java.io.*;
4. import java.util.ArrayList;
5. import java.util.List;
6. import java.util.Scanner;
8. public class RadixSort {
9.     //用最低位排序法最简单
10.     public static void LSD(int[] num) {
11.         //十个队列，queues.get(2);表示拿出第三个队列
12.         List<MyQueue<Integer>> queues = new ArrayList<>();
13.         //最开始建10个队列
14.         for (int i = 0; i < 10; i++) {
15.             MyQueue<Integer> queue = new MyQueue<>();
16.             queues.add(queue);
17.         }
18.         int digits = getNumDigits(num);
19.         int mode = 1;
20.         while (digits != 0) {
21.             //入队
22.             for (int value : num) {
23.                 queues.get((value / mode) % 10).add(value);
24.             }
25.             //出队,k表示数组中的
26.             int k = 0;
27.             //j表示第几个队列
28.             for(int j = 0; j < 10; j++){
29.                 while(!queues.get(j).isEmpty()){
30.                     num[k] = queues.get(j).poll();
31.                     k++;
32.                 }
33.             }
34.             digits--;//位上移
35.             mode = mode * 10;
36.         }
37.     }
39.     public static void LSD(String[] str) {
40.         //52个队列，queues.get(2);表示拿出第三个队列
41.         List<MyQueue<String>> queues = new ArrayList<>();
42.         //最开始建52个队列
43.         for (int i = 0; i < 52; i++) {
44.             MyQueue<String> queue = new MyQueue<>();
45.             queues.add(queue);
46.         }
47.         int digits = str[0].length();//等长字符的长度
48.         //位数
49.         while (digits != 0) {
50.             //入队
51.             for (String letter : str) {
52.                 queues.get(getSize(getCharByDigits(digits,letter))).add(letter);
53.             }
54.             //出队,k表示数组中的
55.             int k = 0;
56.             //j表示第几个队列
57.             for(int j = 0; j < 52; j++){
58.                 while(!queues.get(j).isEmpty()){
59.                     str[k] = queues.get(j).poll();
60.                     k++;
61.                 }
62.             }
63.             digits--;//位上移
64.         }
65.     }
67.     private static int getNumDigits(int[] num) {//获得最大的数的位数
68.         int max = num[0];//最大的数
69.         int digits = 0;//位数
70.         for (int i = 0; i < num.length; i++) {
71.             if (num[i] > max) max = num[i];
72.         }
73.         while (max / 10 != 0) {
74.             digits++;
75.             max = max / 10;
76.         }
77.         if (max % 10 != 0) {
78.             digits++;
79.         }
80.         return digits;
81.     }
83.     //根据几位数返回char
84.     private static char getCharByDigits(int digit, String string){
85.         char[] charArray = string.toCharArray();
86.         return charArray[digit - 1];
87.     }
89.     private static int getSize(char letter){
90.         if('a' <= letter && letter <= 'z'){
91.             //a返回的是0
92.             return letter - 97;
93.         } else if ('A' <= letter && letter <= 'Z') {
94.             //A返回的是26
95.             return letter - 65 + 26;
96.         }
97.         return -1;
98.     }
100.     public static void main(String[] args) {
101.         String inputFilePath1 = "D:\\develop\\projects\\dataStructure\\homework02\\src\\Homework04\\radixSort1.txt";
102.         String outputFilePath1 = "D:\\develop\\projects\\dataStructure\\homework02\\src\\Homework04\\sorted_numbers.txt";
103.         String inputFilePath2 = "D:\\develop\\projects\\dataStructure\\homework02\\src\\Homework04\\radixSort2.txt";
104.         String outputFilePath2 = "D:\\develop\\projects\\dataStructure\\homework02\\src\\Homework04\\sorted_letters.txt";
106.         int[] numbers = readNumbersFromFile(inputFilePath1);
107.         String[] letters = readStringsFromFile(inputFilePath2);
109.         // 打印原始数组
110.         System.out.println("原始数组:");
111.         for (int number : numbers) {
112.             System.out.print(number + " ");
113.         }
114.         System.out.println();
116.         // 进行基数排序
117.         long startTime = System.nanoTime(); // 记录开始时间
118.         LSD(numbers);
119.         long endTime = System.nanoTime(); // 记录结束时间
121.         // 打印排序后的数组
122.         System.out.println("排序后的数组:");
123.         for (int number : numbers) {
124.             System.out.print(number + " ");
125.         }
126.         System.out.println();
128.         // 计算并打印执行时间
129.         double duration = (double) (endTime - startTime) / 1000000;
130.         System.out.println("LSD(numbers)的执行时间为: " + duration + "毫秒");
132.         // 将排序结果输出到文件
133.         writeNumbersToFile(numbers, outputFilePath1);
134.         System.out.println("排序结果已写入文件: " + outputFilePath1);
136.         // 打印原始字母数组
137.         System.out.println("原始字母数组:");
138.         for (String letter : letters) {
139.             System.out.print(letter + " ");
140.         }
141.         System.out.println();
143.         // 进行基数排序
144.         startTime = System.nanoTime(); // 记录开始时间
145.         LSD(letters);
146.         endTime = System.nanoTime(); // 记录结束时间
148.         // 打印排序后的字母数组
149.         System.out.println("排序后的字母数组:");
150.         for (String letter : letters) {
151.             System.out.print(letter + " ");
152.         }
153.         System.out.println();
155.         // 计算并打印执行时间
156.         duration = (double) (endTime - startTime) / 1000000;
157.         System.out.println("LSD(letters)的执行时间为: " + duration + "毫秒");
159.         // 将排序结果输出到文件
160.         writeStringsToFile(letters, outputFilePath2);
161.         System.out.println("排序结果已写入文件: " + outputFilePath2);
162.     }
164.     private static int[] readNumbersFromFile(String filePath) {
165.         int[] numbers = null;
166.         try {
167.             File file = new File(filePath);
168.             Scanner scanner = new Scanner(file);
169.             //计算文件中有多少个数
170.             int count = 0;
171.             while (scanner.hasNext()) {
172.                 if (scanner.hasNextInt()) {
173.                     scanner.nextInt();
174.                     count++;
175.                 } else {
176.                     scanner.next();
177.                 }
178.             }
179.             scanner.close();
180.             //把数字填入数组
181.             numbers = new int[count];
182.             scanner = new Scanner(file);
183.             int index = 0;
184.             while (scanner.hasNext()) {
185.                 if (scanner.hasNextInt()) {
186.                     numbers[index] = scanner.nextInt();
187.                     index++;
188.                 } else {
189.                     scanner.next();
190.                 }
191.             }
192.             scanner.close();
193.         } catch (FileNotFoundException e) {
194.             e.printStackTrace();
195.         }
196.         return numbers;
197.     }
199.     private static String[] readStringsFromFile(String filePath) {
200.         String[] strings = null;
201.         try {
202.             File file = new File(filePath);
203.             Scanner scanner = new Scanner(file);
204.             // 计算文件中有多少个字符串
205.             int count = 0;
206.             while (scanner.hasNext()) {
207.                 if (scanner.hasNext()) {
208.                     scanner.next();
209.                     count++;
210.                 } else {
211.                     scanner.next();
212.                 }
213.             }
214.             scanner.close();
215.             // 把字符串填入数组
216.             strings = new String[count];
217.             scanner = new Scanner(file);
218.             int index = 0;
219.             while (scanner.hasNext()) {
220.                 if (scanner.hasNext()) {
221.                     strings[index] = scanner.next();
222.                     index++;
223.                 } else {
224.                     scanner.next();
225.                 }
226.             }
227.             scanner.close();
228.         } catch (FileNotFoundException e) {
229.             e.printStackTrace();
230.         }
231.         return strings;
232.     }
234.     private static void writeNumbersToFile(int[] numbers, String filePath) {
235.         try {
236.             PrintWriter writer = new PrintWriter(filePath);
237.             int count = 0;
238.             for (int number : numbers) {
239.                 writer.print(number + " ");
240.                 count++;
241.                 if (count % 50 == 0) {
242.                     writer.println();
243.                 }
244.             }
245.             writer.close();
246.         } catch (FileNotFoundException e) {
247.             e.printStackTrace();
248.         }
249.     }
251.     private static void writeStringsToFile(String[] strings, String filePath) {
252.         try {
253.             PrintWriter writer = new PrintWriter(filePath);
254.             int count = 0;
255.             for (String str : strings) {
256.                 writer.print(str + " ");
257.                 count++;
258.                 if (count % 50 == 0) {
259.                     writer.println();
260.                 }
261.             }
262.             writer.close();
263.         } catch (FileNotFoundException e) {
264.             e.printStackTrace();
265.         }
266.     }
268. }