XJTUSE 数据结构与算法第三次作业——任务1_xjtu数据结构实验-优快云博客

本文链接：https://blog.youkuaiyun.com/woshihlf/article/details/143443707

任务1

题目

二叉检索树即 BST，是利用二叉树的非线性关系，结合数据之间的大小关系进行存储的一种用于检索数据的数据结构。一般情况下，对信息进行检索时，都需要指定检索关键码（Key），根据该关键字找到所需要的信息（比如学生信息里关键码是学号，而姓名等信息就是该关键码对应的信息），所以当提到检索时，都会有“键值对”这个概念，用(key,value)表示键值和对应信息的关系。

下面的二叉检索树的 ADT 在描述时，依然使用了模板类的方法，并且在这次描述中，使用了两个模板参数 K 和 V（这表明 key 和 value 可以为不同类型的数据）。在本次任务的测试文件中，key 和 value 都是 String 类型，对模板参数运用有困难的同学，可以直接设定 key 和 value 的类型为 String。

在本次实验中，主要完成的任务是：

1、为指定的 BST ADT实现数据结构。

2、用给定的输入数据文件验证所实现的数据结构是否正确。

为了方便进行测试验证，对BST 的各种操作指定了相应的命令符号，具体的符号含义如下：

实验完成之后，必须通过实验中提供的测试用例。借助测试用例的运行结果，用来检查所撰写的代码功能是否正确。

测试用例中的每一行的内容都类似于上表中的每一行“命令行内容”列中所指示的内容。要求每执行一行，就调用 List 接口中的 showStructure 行为，用以验证该命令行的执行是否正确。

每行“命令行内容”都不是独立的，是针对同一个 List 类型的对象实例运行的结果。实验包里包括了个文件，一个是“list_testcase.txt”，其内包含了测试用例；另一个是“list_result.txt”，其内包含了对应测试用例的运行结果。

数据设计

这个BST的实现是一个通用的、基于泛型的二叉搜索树，支持任何实现了Comparable接口的键类型。递归是实现插入、删除、搜索和更新等操作的主要手段。

BSTNode类包括K key：键，用于比较节点的大小关系；V value：值，存储在节点中的数据；BSTNode<K, V> left：左子节点；BSTNode<K, V> right：右子节点。

static class BSTNode<K extends Comparable<K>, V> {
K key;
V value;
BSTNode<K, V> left;
BSTNode<K, V> right;
public BSTNode(K key, V value, BSTNode<K, V> left, BSTNode<K, V> right) {
this.key = key;
this.value = value;
this.left = left;
this.right = right;
}
}

insert(K key, V value) 方法接受一个键值对作为输入，将其插入到二叉搜索树中。方法首先检查输入的键和值是否为 null，如果是则抛出异常。然后，调用 doInsert 方法来执行实际的插入操作，同时更新根节点。

doInsert 方法是一个私有的递归方法，它接受一个节点、一个键和一个值作为输入，并返回更新后的节点。在 doInsert(BSTNode<K, V> node, K key, V value) 方法中，首先检查节点是否为 null。如果节点为 null，说明当前位置是一个合适的插入点，于是创建一个新的节点，并将键值对存储在新节点中，然后返回新节点。如果节点不为 null，那么需要根据键的大小关系选择向左子树或右子树递归插入。如果键小于当前节点的键，则递归调用 doInsert 方法，传入当前节点的左子节点，键和值，并将返回的结果赋值给当前节点的左子节点。如果键大于当前节点的键，则递归调用 doInsert 方法，传入当前节点的右子节点，键和值，并将返回的结果赋值给当前节点的右子节点。如果键等于当前节点的键，则更新当前节点的值。

时间复杂度分析：对于 insert(K key, V value) 方法，除了调用 doInsert 方法外，其他操作都是常数时间操作，不会对时间复杂度产生影响。而 doInsert 方法是一个递归方法，其时间复杂度取决于树的高度。在平衡的情况下，二叉搜索树的高度可以近似为 log(n)，其中 n 是树中节点的数量。因此，在平衡的情况下，insert 方法的时间复杂度为 O(log n)。然而，如果二叉搜索树不平衡，即树的高度接近于 n，那么插入操作的时间复杂度可能接近于 O(n)。

@Override
public void insert(K key, V value) {
if (key == null) {
throw new NullPointerException("Key cannot be null");
}
if (value == null) {
throw new NullPointerException("Value cannot be null");
}
root = doInsert(root, key, value); // 更新根节点
}
private BSTNode<K, V> doInsert(BSTNode<K, V> node, K key, V value) {
if (node == null) {
return new BSTNode<>(key, value, null, null); // 创建新节点并返回
}
if (key.compareTo(node.key) < 0) {
node.left = doInsert(node.left, key, value); // 递归插入左子树
} else if (key.compareTo(node.key) > 0) {
node.right = doInsert(node.right, key, value); // 递归插入右子树
} else {
node.value = value; // 更新节点值
}
return node;
}

remove(K key) 方法接受一个键作为输入，从二叉搜索树中删除对应的节点，并返回删除节点的值。方法首先将 removeValue 设置为 null，然后检查输入的键是否为 null，如果是则抛出异常。接着，调用 removeHelp 方法执行实际的删除操作，并更新根节点。最后，返回删除节点的值。

在 removeHelp(BSTNode<K, V> root, K key) 方法中，首先检查根节点是否为 null。如果根节点为 null，说明树为空，直接返回 null。接下来，根据键和根节点的键的大小关系，选择向左子树或右子树递归删除。如果键小于根节点的键，则递归调用 removeHelp 方法，并将返回的结果赋值给根节点的左子节点。如果键大于根节点的键，则递归调用 removeHelp 方法，并将返回的结果赋值给根节点的右子节点。如果键等于根节点的键，那么需要考虑不同情况下的节点删除操作：

如果根节点没有左子节点，将 removeValue 设置为根节点的值，然后将根节点指向其右子节点，完成删除操作。

如果根节点没有右子节点，将 removeValue 设置为根节点的值，然后将根节点指向其左子节点，完成删除操作。

如果根节点既有左子节点又有右子节点，需要找到右子树中的最小节点（即右子树中最左边的节点），将其键和值替换到根节点中，然后递归地删除右子树中的最小节点，并将返回的结果赋值给根节点的右子节点。

此外，还有两个辅助方法 getMinNode 和 removeMinNode。getMinNode 方法用于获取指定树中的最小节点，它通过递归地向左子树寻找最小节点，并返回结果。removeMinNode 方法用于删除指定树中的最小节点，它通过递归地删除左子树中的最小节点，并将返回的结果赋值给当前节点的左子节点。

时间复杂度分析：对于 remove(K key) 方法，除了调用 removeHelp 方法外，其他操作都是常数时间操作，不会对时间复杂度产生影响。而 removeHelp 方法是一个递归方法，其时间复杂度取决于树的高度。在平衡的情况下，二叉搜索树的高度可以近似为 log(n)，其中 n 是树中节点的数量。因此，在平衡的情况下，删除操作的时间复杂度为 O(log n)。然而，如果二叉搜索树不平衡，即树的高度接近于 n，那么删除操作的时间复杂度可能接近于 O(n)。

@Override
public V remove(K key) {
removeValue = null;
if (key == null) {
throw new NullPointerException("Key cannot be null");
}
root = removeHelp(root, key);
return removeValue;
}
private BSTNode<K, V> removeHelp(BSTNode<K, V> root, K key) {
if (root == null)
return null;
if (key.compareTo(root.key) < 0) {
root.left = removeHelp(root.left, key);
} else if (key.compareTo(root.key) > 0) {
root.right = removeHelp(root.right, key);
} else {
if (root.left == null) {
removeValue = root.value;
root = root.right;
} else if (root.right == null) {
removeValue = root.value;
root = root.left;
} else {
BSTNode<K, V> minNode = getMinNode(root.right);
removeValue = root.value;
root.key = minNode.key;
root.value = minNode.value;
root.right = removeMinNode(root.right);
}
}
return root;
}
private BSTNode<K, V> getMinNode(BSTNode<K, V> root) {
if (root.left == null)
return root;
else
return getMinNode(root.left);
}
private BSTNode<K, V> removeMinNode(BSTNode<K, V> root) {
if (root.left == null) {
return root.right;
}
root.left = removeMinNode(root.left);
return root;
}

search(K key) 方法接受一个键作为输入，从二叉搜索树中查找对应的值，并返回该值。方法首先检查输入的键是否为 null，如果是则抛出异常。接下来，调用私有方法 search，并传入根节点和键进行递归查找。最后，返回查找结果。

在 search(BSTNode<K, V> root, K key) 方法中，首先检查根节点是否为 null。如果根节点为 null，说明树为空，直接返回 null。接下来，根据键和根节点的键的大小关系，选择向左子树或右子树递归查找。如果键小于根节点的键，则递归调用 search 方法，并传入根节点的左子节点和键进行查找。如果键大于根节点的键，则递归调用 search 方法，并传入根节点的右子节点和键进行查找。如果键等于根节点的键，则找到了对应的节点，直接返回该节点的值。

时间复杂度分析：对于 search(K key) 方法，除了调用 search 方法外，其他操作都是常数时间操作，不会对时间复杂度产生影响。而 search 方法是一个递归方法，其时间复杂度取决于树的高度。在平衡的情况下，二叉搜索树的高度可以近似为 log(n)，其中 n 是树中节点的数量。因此，在平衡的情况下，搜索操作的时间复杂度为 O(log n)。然而，如果二叉搜索树不平衡，即树的高度接近于 n，那么搜索操作的时间复杂度可能接近于 O(n)。

@Override
public V search(K key) {
if (key == null) {
throw new NullPointerException("Key cannot be null");
}
return search(root, key);
}
private V search(BSTNode<K, V> root, K key) {
if (root == null)
return null;
if (key.compareTo(root.key) < 0)
return search(root.left, key);//小于当前key值则往左子树查找
if (key.compareTo(root.key) > 0)
return search(root.right, key);//大于当前key值则往右子树查找
return root.value;//找到值
}

update(K key, V value) 方法接受一个键和一个值作为输入，用于更新二叉搜索树中指定键对应的节点的值，并返回一个布尔值表示更新是否成功。方法首先检查输入的键和值是否为 null，如果是则抛出异常。接下来，调用私有方法 update，并传入根节点、键和值进行递归更新。最后，返回更新结果。

在 update(BSTNode<K, V> root, K key, V value) 方法中，首先检查键是否等于根节点的键。如果相等，说明找到了要更新的节点，将节点的值更新为输入的值，并返回 true 表示更新成功。如果键小于根节点的键，则递归调用 update 方法，并传入根节点的左子节点、键和值进行更新。如果键大于根节点的键，则递归调用 update 方法，并传入根节点的右子节点、键和值进行更新。如果以上情况都不满足，说明树中不存在指定的键，返回 false 表示更新失败。

时间复杂度分析：对于 update(K key, V value) 方法，除了调用 update 方法外，其他操作都是常数时间操作，不会对时间复杂度产生影响。而 update 方法是一个递归方法，其时间复杂度取决于树的高度。在平衡的情况下，二叉搜索树的高度可以近似为 log(n)，其中 n 是树中节点的数量。因此，在平衡的情况下，更新操作的时间复杂度为 O(log n)。然而，如果二叉搜索树不平衡，即树的高度接近于 n，那么更新操作的时间复杂度可能接近于 O(n)。

@Override
public boolean update(K key, V value) {
if (key == null) {
throw new NullPointerException("Key cannot be null");
}
if (value == null) {
throw new NullPointerException("Value cannot be null");
}
return update(root, key, value);
}
public boolean update(BSTNode<K, V> root, K key, V value) {
if (key.compareTo(root.key) == 0) {
root.value = value;
return true;
}
if (key.compareTo(root.key) < 0)
return update(root.left, key, value);
if (key.compareTo(root.key) > 0)
return update(root.right, key, value);
return false;
}

isEmpty方法：判断树是否为空，即根节点是否为null。时间复杂度为O(1)。

clear方法：将根节点置为null，清空整个树。时间复杂度为O(1)。

@Override
public boolean isEmpty() {
return root == null;
}
@Override
public void clear() {
root = null;
}

showStructure(PrintWriter pw) 方法用于将二叉搜索树的结构信息输出到给定的 PrintWriter。方法首先调用 countNodes 方法获取二叉搜索树的节点数量，然后调用 getHeight 方法获取二叉搜索树的高度。接下来，输出一些描述性信息，包括节点数量和树的高度。最后，通过调用 pw.flush() 来确保输出立即被写入到目标中。

countNodes(BSTNode<K, V> node) 方法用于递归计算以给定节点为根的二叉搜索树的节点数量。如果节点为 null，则返回 0。否则，递归调用 countNodes 方法计算左子树和右子树的节点数量，并将其加上当前节点的数量（1），然后返回结果。

getHeight(BSTNode<K, V> node) 方法用于递归计算以给定节点为根的二叉搜索树的高度。如果节点为 null，则返回 0。否则，递归调用 getHeight 方法计算左子树和右子树的高度，并取两者中的最大值，然后加上当前节点的高度（1），最后返回结果。

时间复杂度分析：countNodes 和 getHeight 方法都是递归方法，其时间复杂度取决于树的高度。在平衡的情况下，二叉搜索树的高度可以近似为 log(n)，其中 n 是树中节点的数量。因此，这两个方法的时间复杂度为 O(log n)。需要注意的是，这里的时间复杂度是在遍历整个树的情况下。对于 showStructure 方法，除了调用 countNodes 和 getHeight 方法外，其他操作都是常数时间操作，不会对时间复杂度产生影响。

@Override
public void showStructure(PrintWriter pw) {
int numberOfNode = countNodes(root);
int height = getHeight(root);
pw.println("-----------------------------");
pw.print("There are ");
pw.print(numberOfNode);
pw.println(" nodes in this BST.");
pw.print("The height of this BST is ");
pw.print(height);
pw.println(".");
pw.println("-----------------------------");
//使用 pw.flush() 是为了确保 showStructure 方法中的输出被立即写入到目标中，而不是等待缓冲区满或程序结束时才进行写入。
pw.flush();
}
private int countNodes(BSTNode<K, V> node) {
if (node == null) {
return 0;
}
int leftCount = countNodes(node.left);
int rightCount = countNodes(node.right);
return 1 + leftCount + rightCount;
}
private int getHeight(BSTNode<K, V> node) {
if (node == null) {
return 0;
}
int leftHeight = getHeight(node.left);
int rightHeight = getHeight(node.right);
return 1 + Math.max(leftHeight, rightHeight);
}

printInorder(PrintWriter pw) 方法用于将二叉搜索树按照中序遍历的顺序输出到给定的 PrintWriter。首先，方法检查传入的 PrintWriter 是否为 null，如果是，则抛出 NullPointerException。接下来，调用私有方法 inorderTraversal，并传入根节点和 PrintWriter 进行中序遍历输出。

inorderTraversal(BSTNode<K, V> node, PrintWriter pw) 方法是一个递归方法，用于实现中序遍历。如果当前节点不为 null，则先递归调用 inorderTraversal 方法遍历当前节点的左子树，然后将当前节点的键和值输出到 PrintWriter，最后再递归调用 inorderTraversal 方法遍历当前节点的右子树。通过这种方式，可以按照中序遍历的顺序输出二叉搜索树的节点。

时间复杂度分析：中序遍历的时间复杂度取决于树的节点数量。在最坏的情况下，即二叉搜索树是一个完全不平衡的链表时，需要遍历所有的节点，时间复杂度为 O(n)。在平衡的情况下，二叉搜索树的高度可以近似为 log(n)，其中 n 是树中节点的数量。

@Override
public void printInorder(PrintWriter pw) {
if (pw == null) {
throw new NullPointerException("PrintWriter不能为空");
}
inorderTraversal(root, pw);
}
private void inorderTraversal(BSTNode<K, V> node, PrintWriter pw) {
if (node != null) {
inorderTraversal(node.left, pw);
pw.println("[" + node.key + " --- <" + node.value + ">]");
inorderTraversal(node.right, pw);
}
}

算法设计

当实现了BST的数据结构后，剩下比较难办的就是怎么用StreamTokenizer实现命令行。

每当我们输入一个回车，程序都会相应的作出一系列动作，那么我们可以把根据行读入，根据输入的内容做出回应。

String line;
while ((line = br.readLine()) != null) {
executeCommand(bstTree, line);
writer.flush(); // 刷新PrintWriter的缓冲区
}

为了方便起见，我们把读取标记并进行相对应的动作用方法抽离出来：

private static <K extends Comparable<K>, V> void executeCommand(BSTTree<K, V> bstTree, String line) throws IOException {
StreamTokenizer st = new StreamTokenizer(new StringReader(line));
int token = st.nextToken();
while (token != StreamTokenizer.TT_EOF) {
char command = (char) st.ttype;
switch (command) {
case '+' -> {
......
}
case '-' -> {
......
}
......
}
token = st.nextToken();
}
}

当读取到+时，分别读取+后面的Key和Value并调用bsttree的insert方法。在bsttree插入对应的key和value。

case '+' -> {
//+( conflagration , "n．建筑物或森林大火" )
st.nextToken();
st.nextToken();
K key = (K) st.sval;
st.nextToken();
st.nextToken();
V value = (V) st.sval;
bstTree.insert(key, value);
}

当读取到-时，读取-后面的Key并调用bsttree的remove方法。在bsttree删除对应的key和value，并根据是否删除成功输出对应的语句。

case '-' -> {
st.nextToken();
st.nextToken();
K key = (K) st.sval;
V value = bstTree.remove(key);
if (value == null) {
writer.println("remove unsuccess ---" + key);
} else {
writer.println("remove success ---" + key + " " + value);
}
}

当读取到？时，读取？后面的Key并调用bsttree的search方法。在bsttree查询对应的key和value，并根据是否查询成功输出对应的语句。

case '?' -> {
st.nextToken();
st.nextToken();
K key = (K) st.sval;
V value = bstTree.search(key);
if (value == null) {
writer.println("search unsuccess ---" + key);
} else {
writer.println("search success ---" + key + " " + value);
}
}

当读取到=时，分别读取=后面的key和value并调用bsttree的update方法。在bsttree更新对应的key和value，并输出更新成功的语句。

case '=' -> {
st.nextToken();
st.nextToken();
K key = (K) st.sval;
st.nextToken();
st.nextToken();
V value = (V) st.sval;
bstTree.update(key, value);
writer.println("update success ---" + key + " " + value);
}

当读取到#就调用showStructure方法。

case '#' ->bstTree.showStructure(writer);

最后，我们为了验证输出与标准答案是否一致，还需要一个验文本文件比较器。

package Homework01;
import java.io.BufferedReader;
import java.io.FileReader;
import java.io.IOException;
public class TextFileComparator {
public static boolean compareFiles(String filePath1, String filePath2) {
try (BufferedReader reader1 = new BufferedReader(new FileReader(filePath1));
BufferedReader reader2 = new BufferedReader(new FileReader(filePath2))) {
String line1, line2;
while ((line1 = reader1.readLine()) != null) {
line2 = reader2.readLine();
if (!line1.equals(line2)) {
return false;
}
}
// Check if file2 has additional lines
return reader2.readLine() == null;
} catch (IOException e) {
e.printStackTrace();
return false;
}
}
public static void main(String[] args) {
String file1 = "D:\\develop\\projects\\dataStructure\\homework03\\file\\homework3_result.txt";
String file2 = "D:\\develop\\projects\\dataStructure\\homework03\\file\\output.txt";
boolean areEqual = compareFiles(file1, file2);
if (areEqual) {
System.out.println("两个文件的内容相同");
} else {
System.out.println("两个文件的内容不同");
}
}
}

运行结果展示

我们可以直接把输出打印在控制台，部分结果如下：

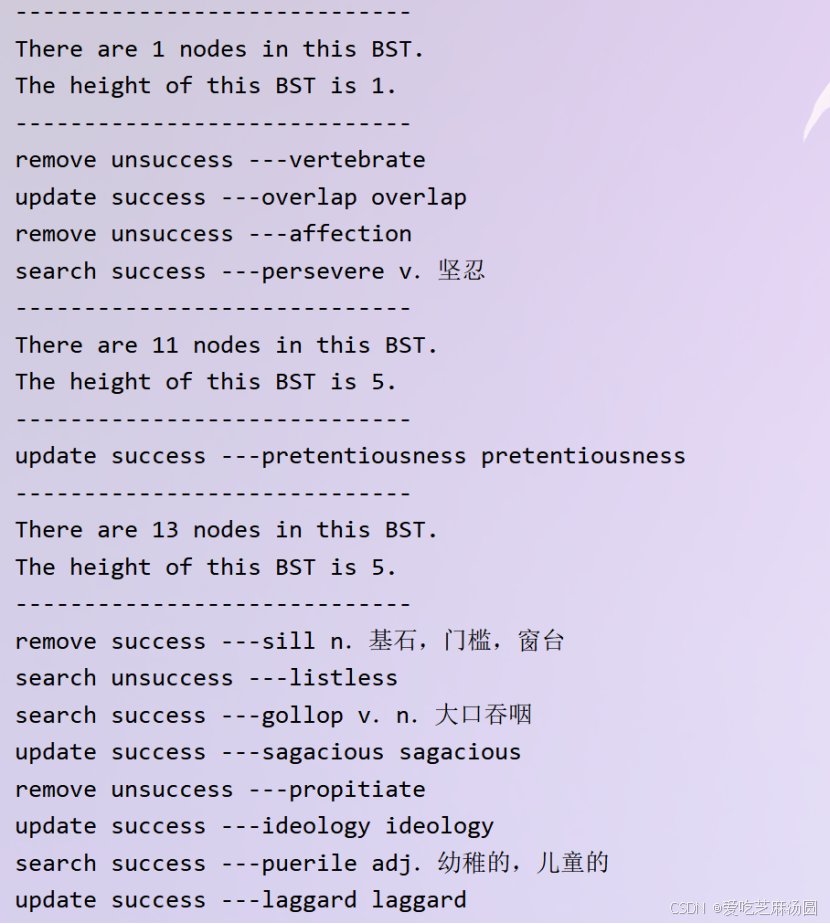
图1 测试结果图（部分）

用人眼无法看出来我们打印在控制台的和答案是否相同，所以我们将PrintWriter打印到一个文件output.txt中，再比较两个文件是否相同。为此写了一个类TextFileComparator。

package Homework01;
import java.io.BufferedReader;
import java.io.FileReader;
import java.io.IOException;
public class TextFileComparator {
public static boolean compareFiles(String filePath1, String filePath2) {
try (BufferedReader reader1 = new BufferedReader(new FileReader(filePath1));
BufferedReader reader2 = new BufferedReader(new FileReader(filePath2))) {
String line1, line2;
while ((line1 = reader1.readLine()) != null) {
line2 = reader2.readLine();
if (!line1.equals(line2)) {
return false;
}
}
// Check if file2 has additional lines
return reader2.readLine() == null;
} catch (IOException e) {
e.printStackTrace();
return false;
}
}
public static void main(String[] args) {
String file1 = "D:\\develop\\projects\\dataStructure\\homework03\\file\\homework3_result.txt";
String file2 = "D:\\develop\\projects\\dataStructure\\homework03\\file\\output.txt";
boolean areEqual = compareFiles(file1, file2);
if (areEqual) {
System.out.println("两个文件的内容相同");
} else {
System.out.println("两个文件的内容不同");
}
}
}

结果如下：

图2 用TextFileComparator文件比较器对比结果图

总结和收获

通过这个实验，首先练习了BST这种数据结构，并复习了泛型的使用，学习了StreamTokenizer类的使用，学会了文件相关的方法和流。收获很大。

附录：

任务1

BST的ADT：

package Homework01;
import java.io.PrintWriter;
public interface BST <K extends Comparable<K>, V>{
/**
* @Precondition 二叉查找树未满。
* Key和value不能为null。
* @Postcondition 向二叉查找树中插入一个新元素(包括键和值)。
* 如果树中已经存在具有相同键值的元素，则使用newElement的value字段更新该元素的value字段。
* @return none
*/
public void insert(K key, V value);
/**
* @Precondition Key不为空。
* @Postcondition 从二叉查找树中删除具有相同键值的元素。
* 如果树中不存在具有相同键值的元素，则返回null。
* 否则，返回元素的value字段。
* @return value
*/
public V remove(K key);
/**
* @Precondition Key不为空。
* @Postcondition 在二叉查找树中查找具有相同键值的元素。
* 如果找到该元素，则返回该元素的value字段。
* 否则，返回null。
* @return value
*/
public V search(K key);
/**
* @Precondition Key和value不能为null。
* @Postcondition 在二叉查找树中查找具有相同键值的元素。
* 如果没有找到该元素，则返回false。
* 否则，用参数的值更新元素的value字段，并返回true。
* @return 布尔值
*/
public boolean update(K key,V value);
/**
* @Precondition none
* @Postcondition
* @return 布尔值
*/
public boolean isEmpty();
/**
* @Precondition none
* @Postcondition 删除二叉查找树中的所有元素。
* @return none
*/
public void clear();
/**
* @Precondition PrintWriter不为null。
* @Postcondition 输出二叉查找树的相关信息。
* 这些信息包括二叉查找树的节点数和高度。
* 输出内容的格式应该是如图2所示(在下一页)。
* @return none
*/
public void showStructure(PrintWriter pw);
/**
* @Precondition PrintWriter不为null。
* @Postcondition 按发送顺序asending order输出二叉查找树中的所有节点。
* 每行输出一个元素。
* 每个元素的输出格式如下:
* [key --- < value >]
* @return none
*/
public void printInorder(PrintWriter pw);
}

BSTtree:

package Homework01;
import java.io.PrintWriter;
public class BSTTree<K extends Comparable<K>, V> implements BST<K, V> {
private V removeValue;
BSTNode<K, V> root;
static class BSTNode<K extends Comparable<K>, V> {
K key;
V value;
BSTNode<K, V> left;
BSTNode<K, V> right;
public BSTNode(K key, V value, BSTNode<K, V> left, BSTNode<K, V> right) {
this.key = key;
this.value = value;
this.left = left;
this.right = right;
}
}
@Override
public void insert(K key, V value) {
if (key == null) {
throw new NullPointerException("Key cannot be null");
}
if (value == null) {
throw new NullPointerException("Value cannot be null");
}
root = doInsert(root, key, value); // 更新根节点
}
private BSTNode<K, V> doInsert(BSTNode<K, V> node, K key, V value) {
if (node == null) {
return new BSTNode<>(key, value, null, null); // 创建新节点并返回
}
if (key.compareTo(node.key) < 0) {
node.left = doInsert(node.left, key, value); // 递归插入左子树
} else if (key.compareTo(node.key) > 0) {
node.right = doInsert(node.right, key, value); // 递归插入右子树
} else {
node.value = value; // 更新节点值
}
return node;
}
@Override
public V remove(K key) {
removeValue = null;
if (key == null) {
throw new NullPointerException("Key cannot be null");
}
root = removeHelp(root, key);
return removeValue;
}
private BSTNode<K, V> removeHelp(BSTNode<K, V> root, K key) {
if (root == null)
return null;
if (key.compareTo(root.key) < 0) {
root.left = removeHelp(root.left, key);
} else if (key.compareTo(root.key) > 0) {
root.right = removeHelp(root.right, key);
} else {
if (root.left == null) {
removeValue = root.value;
root = root.right;
} else if (root.right == null) {
removeValue = root.value;
root = root.left;
} else {
BSTNode<K, V> minNode = getMinNode(root.right);
removeValue = root.value;
root.key = minNode.key;
root.value = minNode.value;
root.right = removeMinNode(root.right);
}
}
return root;
}
private BSTNode<K, V> getMinNode(BSTNode<K, V> root) {
if (root.left == null)
return root;
else
return getMinNode(root.left);
}
private BSTNode<K, V> removeMinNode(BSTNode<K, V> root) {
if (root.left == null) {
return root.right;
}
root.left = removeMinNode(root.left);
return root;
}
@Override
public V search(K key) {
if (key == null) {
throw new NullPointerException("Key cannot be null");
}
return search(root, key);
}
private V search(BSTNode<K, V> root, K key) {
if (root == null)
return null;
if (key.compareTo(root.key) < 0)
return search(root.left, key);//小于当前key值则往左子树查找
if (key.compareTo(root.key) > 0)
return search(root.right, key);//大于当前key值则往右子树查找
return root.value;//找到值
}
@Override
public boolean update(K key, V value) {
if (key == null) {
throw new NullPointerException("Key cannot be null");
}
if (value == null) {
throw new NullPointerException("Value cannot be null");
}
return update(root, key, value);
}
public boolean update(BSTNode<K, V> root, K key, V value) {
if (key.compareTo(root.key) == 0) {
root.value = value;
return true;
}
if (key.compareTo(root.key) < 0)
return update(root.left, key, value);
if (key.compareTo(root.key) > 0)
return update(root.right, key, value);
return false;
}
@Override
public boolean isEmpty() {
return root == null;
}
@Override
public void clear() {
root = null;
}
@Override
public void showStructure(PrintWriter pw) {
int numberOfNode = countNodes(root);
int height = getHeight(root);
pw.println("-----------------------------");
pw.print("There are ");
pw.print(numberOfNode);
pw.println(" nodes in this BST.");
pw.print("The height of this BST is ");
pw.print(height);
pw.println(".");
pw.println("-----------------------------");
//使用 pw.flush() 是为了确保 showStructure 方法中的输出被立即写入到目标中，而不是等待缓冲区满或程序结束时才进行写入。
pw.flush();
}
private int countNodes(BSTNode<K, V> node) {
if (node == null) {
return 0;
}
int leftCount = countNodes(node.left);
int rightCount = countNodes(node.right);
return 1 + leftCount + rightCount;
}
private int getHeight(BSTNode<K, V> node) {
if (node == null) {
return 0;
}
int leftHeight = getHeight(node.left);
int rightHeight = getHeight(node.right);
return 1 + Math.max(leftHeight, rightHeight);
}
@Override
public void printInorder(PrintWriter pw) {
if (pw == null) {
throw new NullPointerException("PrintWriter不能为空");
}
inorderTraversal(root, pw);
}
private void inorderTraversal(BSTNode<K, V> node, PrintWriter pw) {
if (node != null) {
inorderTraversal(node.left, pw);
pw.println("[" + node.key + " --- <" + node.value + ">]");
inorderTraversal(node.right, pw);
}
}
}

SystemInTest：

package Homework01;
import java.io.*;
public class SystemInTest {
private static PrintWriter writer;
public static void main(String[] args) throws IOException {
BSTTree<String, String> bstTree = new BSTTree<>();
InputStreamReader isr = new InputStreamReader(System.in);
BufferedReader br = new BufferedReader(isr);
writer = new PrintWriter(System.out); // 创建PrintWriter对象
String line;
while ((line = br.readLine()) != null) {
executeCommand(bstTree, line);
writer.flush(); // 刷新PrintWriter的缓冲区
}
writer.close(); // 在循环结束后关闭PrintWriter对象
}
//泛型方法
private static <K extends Comparable<K>, V> void executeCommand(BSTTree<K, V> bstTree, String line) throws IOException {
StreamTokenizer st = new StreamTokenizer(new StringReader(line));
int token = st.nextToken();
while (token != StreamTokenizer.TT_EOF) {
char command = (char) st.ttype;
switch (command) {
case '+' -> {
//+( conflagration , "n．建筑物或森林大火" )
st.nextToken();
st.nextToken();
K key = (K) st.sval;
st.nextToken();
st.nextToken();
V value = (V) st.sval;
bstTree.insert(key, value);
}
case '-' -> {
st.nextToken();
st.nextToken();
K key = (K) st.sval;
V value = bstTree.remove(key);
if (value == null) {
writer.println("remove unsuccess ---" + key);
} else {
writer.println("remove success ---" + key + " " + value);
}
}
case '?' -> {
st.nextToken();
st.nextToken();
K key = (K) st.sval;
V value = bstTree.search(key);
if (value == null) {
writer.println("search unsuccess ---" + key);
} else {
writer.println("search success ---" + key + " " + value);
}
}
case '=' -> {
st.nextToken();
st.nextToken();
K key = (K) st.sval;
st.nextToken();
st.nextToken();
V value = (V) st.sval;
bstTree.update(key, value);
writer.println("update success ---" + key + " " + value);
}
case '#' ->
bstTree.showStructure(writer);
}
token = st.nextToken();
}
}
}

FileTest：

package Homework01;
import java.io.*;
public class FileTest {
private static PrintWriter writer;
public static void main(String[] args) throws IOException {
BSTTree<String, String> bstTree = new BSTTree<>();
FileReader fileReader = new FileReader("D:\\develop\\projects\\dataStructure\\homework03\\file\\homework3_testcases.txt");
BufferedReader br = new BufferedReader(fileReader);
writer = new PrintWriter(new FileWriter("D:\\develop\\projects\\dataStructure\\homework03\\file\\output.txt")); // 创建PrintWriter对象，并将输出定向到文件
String line;
while ((line = br.readLine()) != null) {
executeCommand(bstTree, line);
writer.flush(); // 刷新PrintWriter的缓冲区
}
writer.close(); // 在循环结束后关闭PrintWriter对象
br.close(); // 关闭输入流
}
//泛型方法
private static <K extends Comparable<K>, V> void executeCommand(BSTTree<K, V> bstTree, String line) throws IOException {
StreamTokenizer st = new StreamTokenizer(new StringReader(line));
int token = st.nextToken();
while (token != StreamTokenizer.TT_EOF) {
char command = (char) st.ttype;
switch (command) {
case '+' -> {
//+( conflagration , "n．建筑物或森林大火" )
st.nextToken();
st.nextToken();
K key = (K) st.sval;
st.nextToken();
st.nextToken();
V value = (V) st.sval;
bstTree.insert(key, value);
}
case '-' -> {
st.nextToken();
st.nextToken();
K key = (K) st.sval;
V value = bstTree.remove(key);
if (value == null) {
writer.println("remove unsuccess ---" + key);
} else {
writer.println("remove success ---" + key + " " + value);
}
}
case '?' -> {
st.nextToken();
st.nextToken();
K key = (K) st.sval;
V value = bstTree.search(key);
if (value == null) {
writer.println("search unsuccess ---" + key);
} else {
writer.println("search success ---" + key + " " + value);
}
}
case '=' -> {
st.nextToken();
st.nextToken();
K key = (K) st.sval;
st.nextToken();
st.nextToken();
V value = (V) st.sval;
bstTree.update(key, value);
writer.println("update success ---" + key + " " + value);
}
case '#' ->
bstTree.showStructure(writer);
}
token = st.nextToken();
}
}
}

TextFileComparator：

package Homework01;
import java.io.BufferedReader;
import java.io.FileReader;
import java.io.IOException;
public class TextFileComparator {
public static boolean compareFiles(String filePath1, String filePath2) {
try (BufferedReader reader1 = new BufferedReader(new FileReader(filePath1));
BufferedReader reader2 = new BufferedReader(new FileReader(filePath2))) {
String line1, line2;
while ((line1 = reader1.readLine()) != null) {
line2 = reader2.readLine();
if (!line1.equals(line2)) {
return false;
}
}
// Check if file2 has additional lines
return reader2.readLine() == null;
} catch (IOException e) {
e.printStackTrace();
return false;
}
}
public static void main(String[] args) {
String file1 = "D:\\develop\\projects\\dataStructure\\homework03\\file\\homework3_result.txt";
String file2 = "D:\\develop\\projects\\dataStructure\\homework03\\file\\output.txt";
boolean areEqual = compareFiles(file1, file2);
if (areEqual) {
System.out.println("两个文件的内容相同");
} else {
System.out.println("两个文件的内容不同");
}
}
}