XJTUSE 数据结构与算法第一次作业——任务4和任务5

原创 于 2024-11-02 01:33:21 发布 · 881 阅读 · 12 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#算法 #数据结构

任务4

  1. 题目

要求：

n 在同等规模的数据量和数据分布相同下，要做 T 次运行测试，用平均值做为此次测试的结果，用以排除因数据的不同和机器运行当前的状态等因素造成的干扰；（在 SortTest 类型的 test 方法参数中有对每次数据规模下的测试次数的指定）

n 将所有排序算法的运行时间结果用图表的方式进行展示，X 轴代表数据规模，Y 轴代表运行时间。（如果因为算法之间运行时间差异过大而造成显示上的问题，可以通过将运行时间使用取对数的方式调整比例尺）

n 对实验的结果进行总结：从一个算法的运行时间变化趋势和数据规模的变化角度，从同样的数据规模和相同数据分布下不同算法的时间相对差异上等角度进行阐述。
 

  1. 数据设计

在类里面定义static数组储存六种算法面对随机、正序、逆序三种数据分布时运算时间，以及运算时间取对数的数值，然后再作图时取对应的数组即可。

优点是，出错几率小，改动代码较少，有利于后续扩展。

缺点是，每次运行时间长，代码冗余。

  1. 主干代码说明

定义static数组：

    static int[] dataLength;

    static double[] insertion_Random_Time;
    static double[] insertion_Random_Changed_Time;
    static double[] insertion_Sorted_Time;
    static double[] insertion_Sorted_Changed_Time;
    static double[] insertion_Inversed_Time;
    static double[] insertion_Inversed_Changed_Time;

主函数里生成对应的数据：

这里以insertion为例，其余排序稍作改动即可。

        //数据规模为：2的8次方到2的16次方
        dataLength = new int[9];
        for (int i = 8; i < 17; i++) {
            dataLength[i - 8] = (int) Math.pow(2, i);
        }
        //储存时间的数组
        insertion_Random_Time = new double[dataLength.length];
        insertion_Random_Changed_Time = new double[dataLength.length];
        insertion_Sorted_Time = new double[dataLength.length];
        insertion_Sorted_Changed_Time = new double[dataLength.length];
        insertion_Inversed_Time = new double[dataLength.length];
        insertion_Inversed_Changed_Time = new double[dataLength.length];

        //选择排序方法
        SortAlgorithm insertion_Alg = new Insertion();
        for (int i = 0; i < dataLength.length; i++){
            insertion_Random_Time[i] = SortTest.test(insertion_Alg, GenerateData.getRandomData(dataLength[i]), 5);
            insertion_Random_Changed_Time[i] = Math.log(insertion_Random_Time[i]) / Math.log(10);//实现以10为底数

            insertion_Sorted_Time[i] = SortTest.test(insertion_Alg, GenerateData.getSortedData(dataLength[i]), 5);
            insertion_Sorted_Changed_Time[i] = Math.log(insertion_Sorted_Time[i]) / Math.log(10);//实现以10为底数

            insertion_Inversed_Time[i] = SortTest.test(insertion_Alg, GenerateData.getInversedData(dataLength[i]), 5);
            insertion_Inversed_Changed_Time[i] = Math.log(insertion_Inversed_Time[i]) / Math.log(10);//实现以10为底数
        }

作图部分：

对每一个排序算法做图，以insertion为例，其余排序稍作改动即可。

对同一种数据（正序，逆序，随机）做多种排序算法的图：

以随机为例，其他稍作修改即可：

  1. 运行结果展示

每种排序算法在面对不同种类数据类型时：

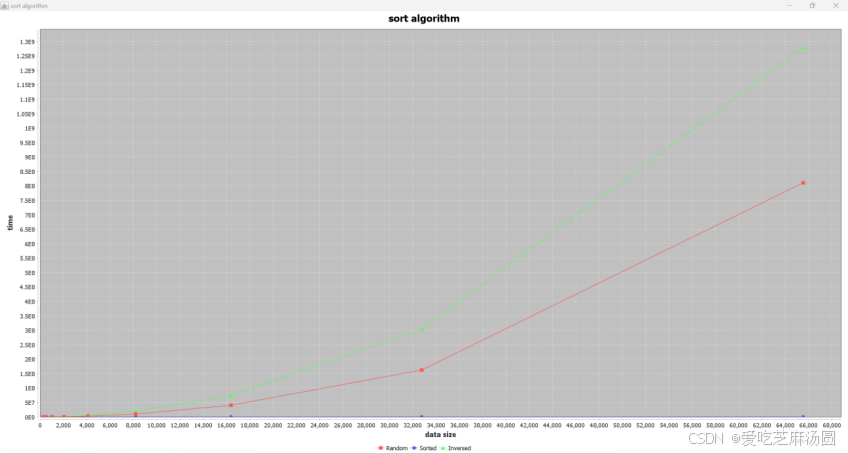
Insertion：

将时间取对数：

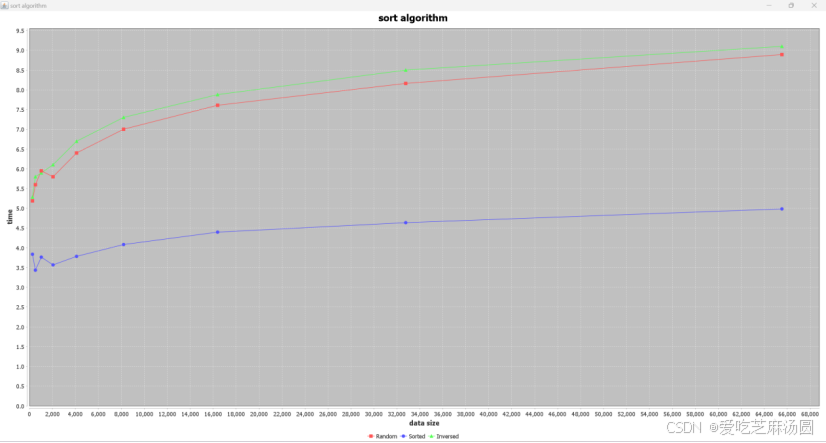
对于insertion算法，插入排序的时间复杂度取决于输入数据的特点。在最好的情况下，即输入数组已经有序时，插入排序的时间复杂度为 O(n)，其中 n 是数组的长度。在最坏的情况下，即输入数组完全逆序时，插入排序的时间复杂度为 O(n^2)。平均情况下，插入排序的时间复杂度也为 O(n^2)。

实验得到的结果与分析一致。

Bubble：

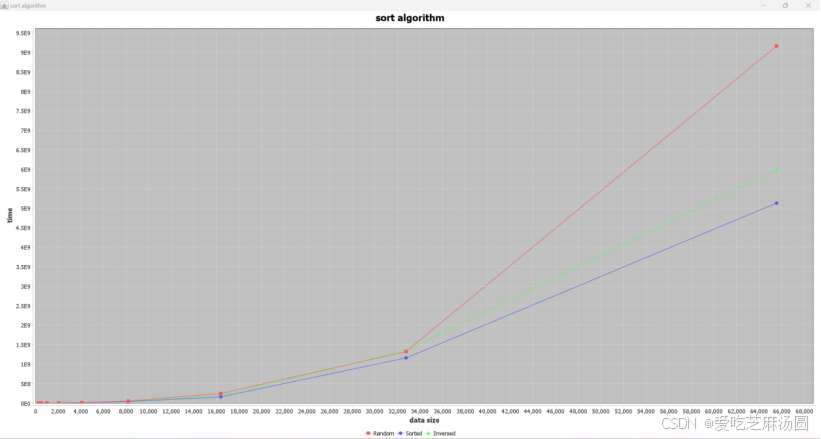
将时间取对数：

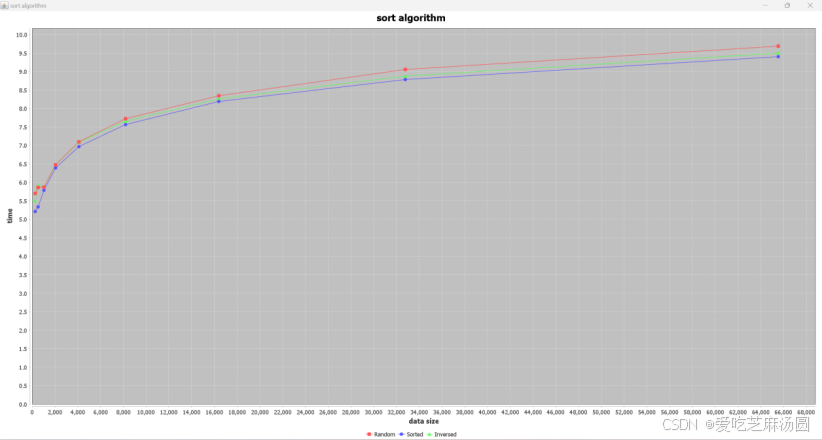
对于bubble算法：在最好的情况下，即输入数组已经有序，冒泡排序只需要进行一次完整的遍历，没有需要交换的元素，因此时间复杂度为 O(n)，其中 n 是数组的长度。在最坏的情况下，即输入数组完全逆序，需要进行 n-1 轮遍历，每轮遍历都需要比较和交换相邻元素，因此总的比较和交换次数为 (n-1) + (n-2) + ... + 2 + 1 = n(n-1)/2。因此，冒泡排序的时间复杂度为 O(n^2)。

但是实验结果表明，在正序、逆序、随机三种情况下，排序的时间在一个数量级，原因在于：如果在冒泡排序中加上一个boolean类型的flag，最开始设为true，如果本次循环没有进行交换，也就是待排序列已经有序，排序已经完成，那么直接跳出循环，如果有进行交换，则在交换后将flag设为false。通过这种优化能显著提高bubble在面对正序的效率。

Selection：

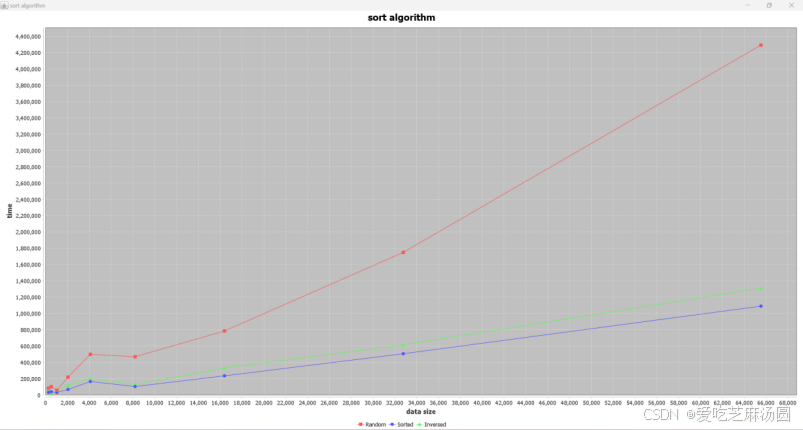
将时间取对数：

选择排序的时间复杂度分析如下：

无论输入数据的顺序如何，选择排序都需要进行 n-1 轮遍历。在每一轮遍历中，需要找到未排序部分的最小（或最大）元素，并将其与未排序部分的第一个元素交换位置。因此，每一轮遍历需要进行 n-i 次比较操作，其中 i 是当前轮次。总的比较次数为 (n-1) + (n-2) + ... + 2 + 1 = n(n-1)/2。选择排序的时间复杂度为 O(n^2)。

需要注意的是，选择排序的时间复杂度与输入数据的顺序无关。即使输入数据已经有序，选择排序仍然需要进行相同数量的比较和交换操作。

还值得注意的是，尽管面对正序、逆序、随机数据时间复杂度相同，但是随机数据花费时间最长，为什么呢？正序数据只需进行比较，不需交换。而逆序数据，第一次需要找n次，将最大和最小元素互换，接着找n-1次，将次大元素和次小元素互换，共n/2轮即可。关键在于，每一轮可以顺手将此时最大元素和最小元素同时归位，比较巧合。一旦稍微改变下数据，就要耗费更多更多时间。

时间结果与分析一致。

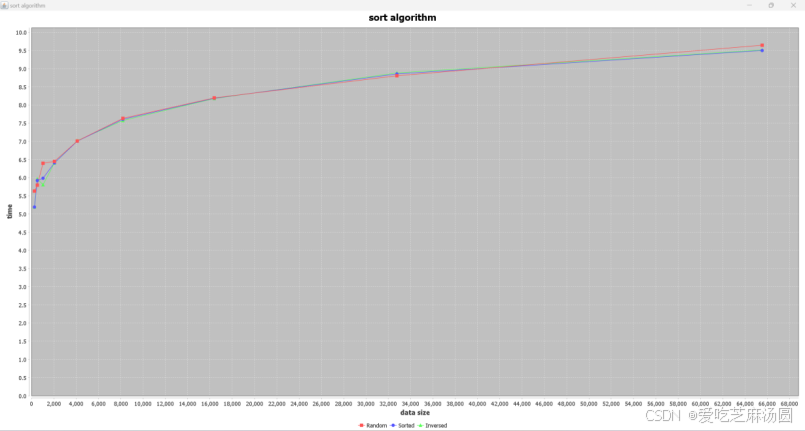
Shell：

将时间取对数：

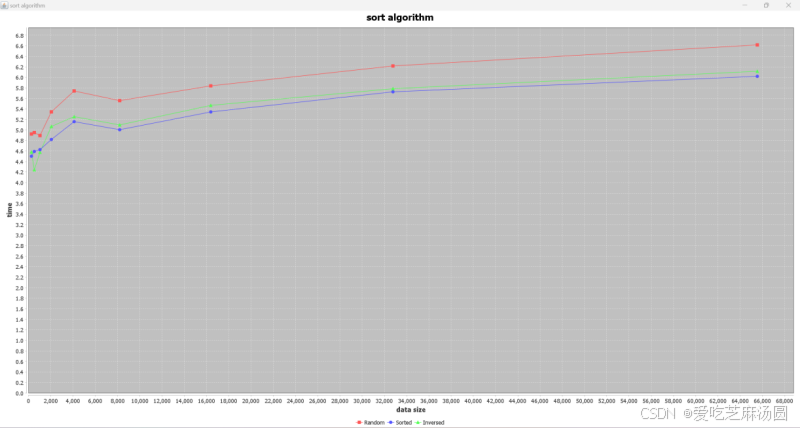
希尔排序的时间复杂度分析比较复杂，因为它涉及到不同的间隔序列和输入数据的特点。总体来说速度相当快。

需要注意的是，希尔排序在面对随机数据时是最慢的，这也和间隔序列有关。

实验和分析一致。

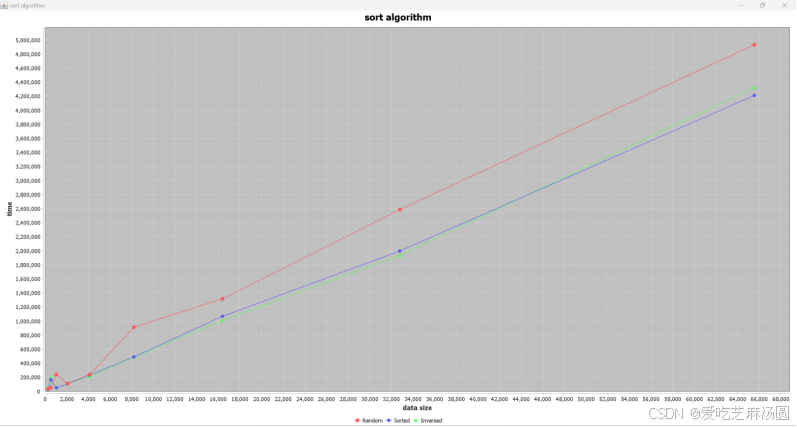
Merge：

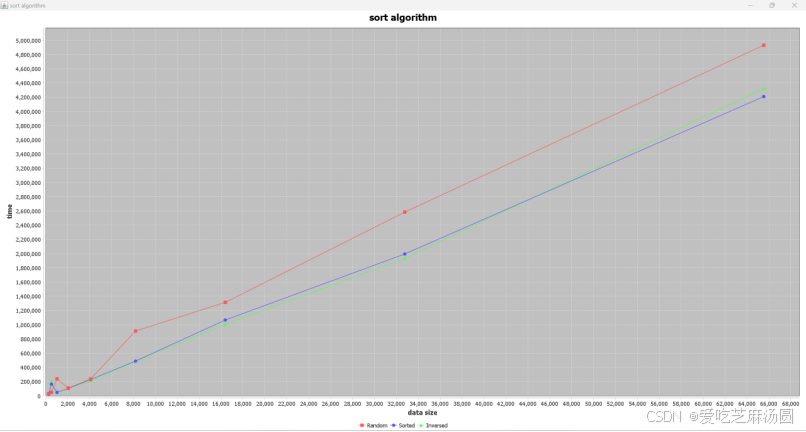
将时间取对数：

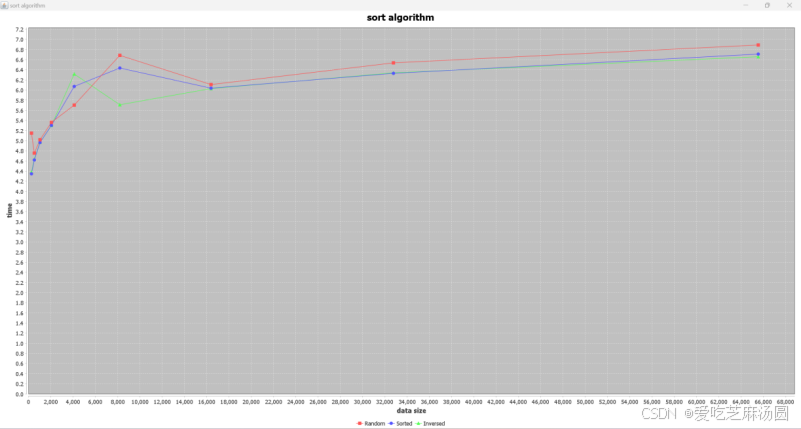
在归并排序的分治过程中，每一次都将待排序数组分成两个子数组，并递归地对这两个子数组进行排序。然后，将两个有序子数组合并成一个有序数组。

分阶段分析归并排序的时间复杂度：

分解阶段：每次将数组划分为两个子数组，需要进行对比和拆分操作，时间复杂度为 O(log n)。

合并阶段：在合并阶段，需要将两个有序子数组合并为一个有序数组。合并操作需要将所有元素进行一次比较，并按顺序放入新的数组中。因此，合并操作的时间复杂度为 O(n)。

由于归并排序每次都将数组划分为两个子数组，并对每个子数组进行递归排序，所以整个排序过程的时间复杂度可以通过递归树来分析。假设待排序数组的长度为 n，则递归树的高度为 log n（每次划分都将数组长度减半）。在每一层递归上，需要进行 O(n) 的比较和合并操作。

实验与分析一致。

Quick：

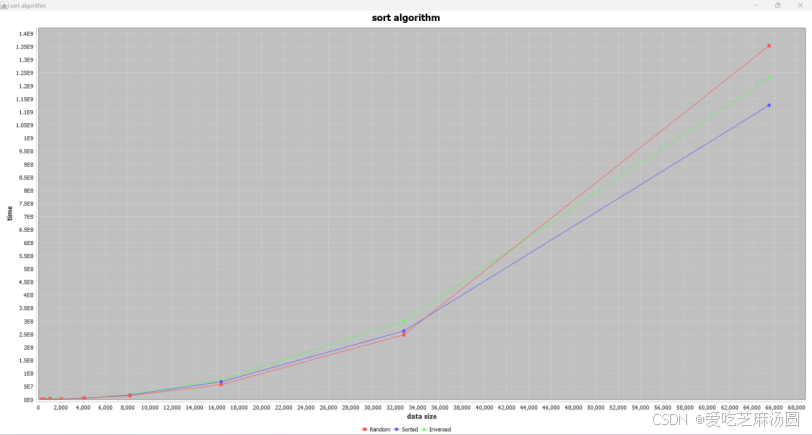
将时间取对数：

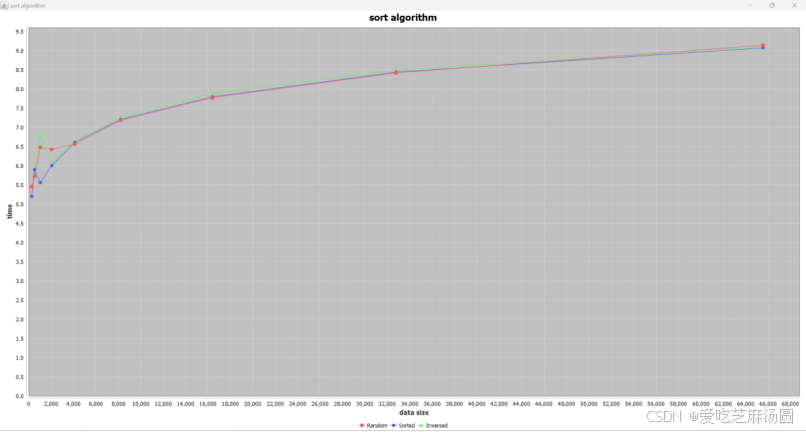
快速排序的时间复杂度分析如下：

在快速排序的分治过程中，每一次都选择一个基准元素，并将数组分成两个子数组。然后，对这两个子数组进行递归排序。

分阶段分析快速排序的时间复杂度：

分解阶段：在分解阶段，需要进行基准元素的选择和数组的划分操作。数组的划分操作需要将所有元素与基准元素进行比较，并将小于等于基准的元素放在一个子数组中，大于基准的元素放在另一个子数组中。分解阶段的时间复杂度为 O(n)。

合并阶段：快速排序的合并阶段实际上是递归地对子数组进行排序。因此，合并阶段的时间复杂度可以通过递归树来分析。

假设待排序数组的长度为 n，则递归树的高度为 log n（每次划分都将数组长度减半）。在每一层递归上，需要进行 O(n) 的划分操作。

由于快速排序是原地排序算法，不需要额外的空间来存储临时数组。

综上所述，快速排序的时间复杂度可以表示为 O(n log n)。在最坏情况下，即每次划分都选择的基准元素都是当前数组中的最小或最大元素时，快速排序的时间复杂度会退化为 O(n^2)。但是，在平均情况下，快速排序的时间复杂度为 O(n log n)，具有较好的性能。

需要注意的是，快速排序是一种不稳定的排序算法，因为在划分阶段可能会改变相等元素的相对顺序。

实验数据较差的原因是，根据题目只用了最简单的快速排序，而优化版本将在第六题给出。

每种数据类型在面对不同种类排序算法时：

Random：

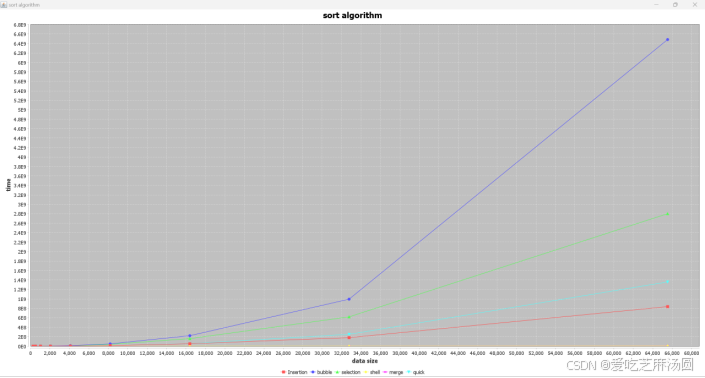
将时间取对数：

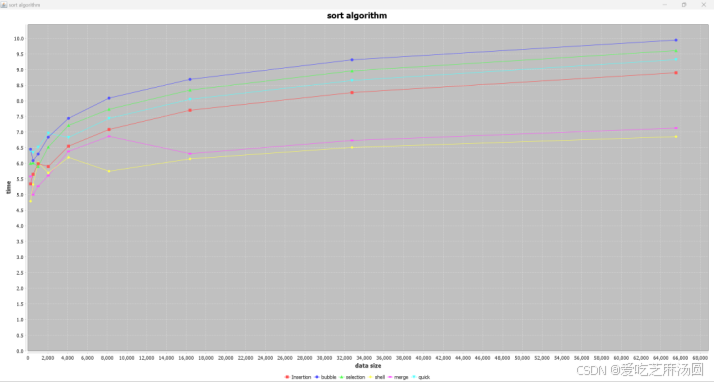
根据对算法的分析，在面对随机数据时，采取最好策略的shell排序快于merge排序，远远快于insert、quick、selection、bubble。

quick慢的原因在于没有优化。

Sorted：

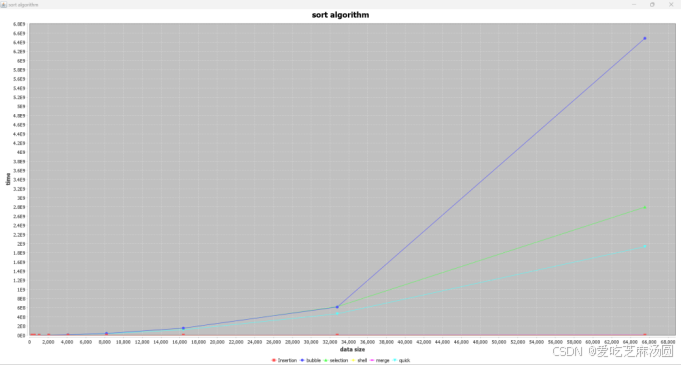
将时间取对数：

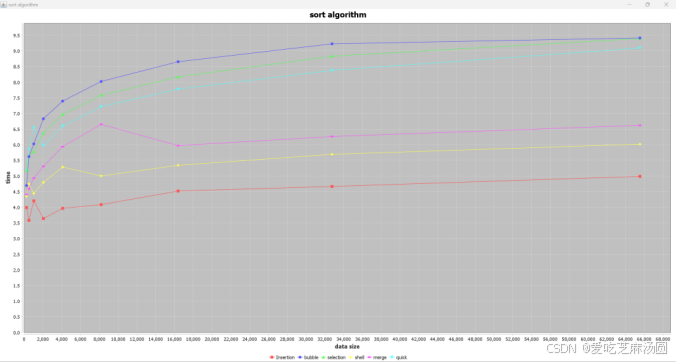
根据对算法的分析，在面对正序数据时，insert算法快于采取最好策略的shell排序，快于merge排序，远远快于quick、selection、bubble。

quick慢的原因在于没有优化。

Inverted：

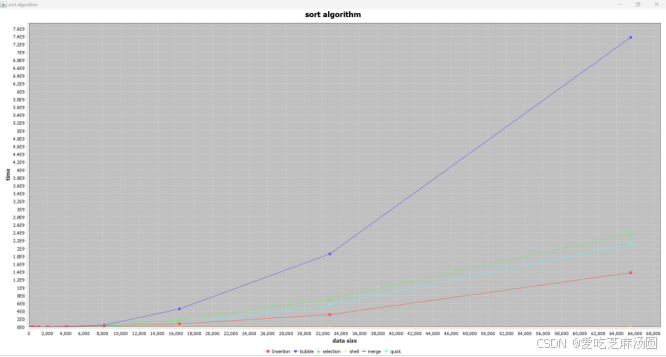
将时间取对数：

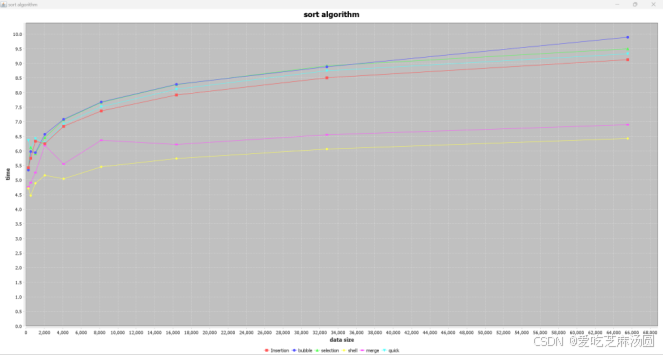
根据对算法的分析，在面对逆序数据时，采取最好策略的shell排序快于merge排序，远远快于insert、quick、selection、bubble。跟面对随机数据时相似。

quick慢的原因在于没有优化。

  1. 分析算法效率

Insertion：

对于insertion算法，插入排序的时间复杂度取决于输入数据的特点。在最好的情况下，即输入数组已经有序时，插入排序的时间复杂度为 O(n)，其中 n 是数组的长度。在最坏的情况下，即输入数组完全逆序时，插入排序的时间复杂度为 O(n^2)。平均情况下，插入排序的时间复杂度也为 O(n^2)。

Bubble：

对于bubble算法：在最好的情况下，即输入数组已经有序，冒泡排序只需要进行一次完整的遍历，没有需要交换的元素，因此时间复杂度为 O(n)，其中 n 是数组的长度。在最坏的情况下，即输入数组完全逆序，需要进行 n-1 轮遍历，每轮遍历都需要比较和交换相邻元素，因此总的比较和交换次数为 (n-1) + (n-2) + ... + 2 + 1 = n(n-1)/2。因此，冒泡排序的时间复杂度为 O(n^2)。

Selection：

无论输入数据的顺序如何，选择排序都需要进行 n-1 轮遍历。在每一轮遍历中，需要找到未排序部分的最小（或最大）元素，并将其与未排序部分的第一个元素交换位置。因此，每一轮遍历需要进行 n-i 次比较操作，其中 i 是当前轮次。总的比较次数为 (n-1) + (n-2) + ... + 2 + 1 = n(n-1)/2。选择排序的时间复杂度为 O(n^2)。

需要注意的是，选择排序的时间复杂度与输入数据的顺序无关。即使输入数据已经有序，选择排序仍然需要进行相同数量的比较和交换操作。

还值得注意的是，尽管面对正序、逆序、随机数据时间复杂度相同，但是随机数据花费时间最长，为什么呢？正序数据只需进行比较，不需交换。而逆序数据，第一次需要找n次，将最大和最小元素互换，接着找n-1次，将次大元素和次小元素互换，共n/2轮即可。关键在于，每一轮可以顺手将此时最大元素和最小元素同时归位，比较巧合。一旦稍微改变下数据，就要耗费更多更多时间。

Shell：

希尔排序的时间复杂度分析比较复杂，因为它涉及到不同的间隔序列和输入数据的特点。总体来说速度相当快。

需要注意的是，希尔排序在面对随机数据时是最慢的，这也和间隔序列有关。

Merge：

在归并排序的分治过程中，每一次都将待排序数组分成两个子数组，并递归地对这两个子数组进行排序。然后，将两个有序子数组合并成一个有序数组。

分阶段分析归并排序的时间复杂度：

分解阶段：每次将数组划分为两个子数组，需要进行对比和拆分操作，时间复杂度为 O(log n)。

合并阶段：在合并阶段，需要将两个有序子数组合并为一个有序数组。合并操作需要将所有元素进行一次比较，并按顺序放入新的数组中。因此，合并操作的时间复杂度为 O(n)。

由于归并排序每次都将数组划分为两个子数组，并对每个子数组进行递归排序，所以整个排序过程的时间复杂度可以通过递归树来分析。假设待排序数组的长度为 n，则递归树的高度为 log n（每次划分都将数组长度减半）。在每一层递归上，需要进行 O(n) 的比较和合并操作。

Quick：

快速排序的时间复杂度分析如下：

在快速排序的分治过程中，每一次都选择一个基准元素，并将数组分成两个子数组。然后，对这两个子数组进行递归排序。

分阶段分析快速排序的时间复杂度：

分解阶段：在分解阶段，需要进行基准元素的选择和数组的划分操作。数组的划分操作需要将所有元素与基准元素进行比较，并将小于等于基准的元素放在一个子数组中，大于基准的元素放在另一个子数组中。分解阶段的时间复杂度为 O(n)。

合并阶段：快速排序的合并阶段实际上是递归地对子数组进行排序。因此，合并阶段的时间复杂度可以通过递归树来分析。

假设待排序数组的长度为 n，则递归树的高度为 log n（每次划分都将数组长度减半）。在每一层递归上，需要进行 O(n) 的划分操作。

由于快速排序是原地排序算法，不需要额外的空间来存储临时数组。

综上所述，快速排序的时间复杂度可以表示为 O(n log n)。在最坏情况下，即每次划分都选择的基准元素都是当前数组中的最小或最大元素时，快速排序的时间复杂度会退化为 O(n^2)。但是，在平均情况下，快速排序的时间复杂度为 O(n log n)，具有较好的性能。

需要注意的是，快速排序是一种不稳定的排序算法，因为在划分阶段可能会改变相等元素的相对顺序。

  1. 总结和收获

了解了不同排序算法面对不同数据的效率比较，实验结果跟想象中有所差异，引人思考。
 

任务5

  1. 题目

完成了任务 3 和任务 4 之后，现要求为 GenerateData 类型再增加一种数据序列的生成方法，该方法要求生成分布不均匀数据序列：1/2 的数据是 0，1/4 的数据是 1，1/8 的数据是 2 和 1/8 的数据是 3。对这种分布不均匀的数据完成如同任务 4 的运行测试，检查这样的数据序列对于排序算法的性能影响。要求同任务 4。（此时，可以将任务 4、任务 5 的运行测试结果做一个纵向比较，用以理解数据序列分布的不同对同一算法性能的影响，如果能从每个排序算法的过程去深入分析理解则更好。）

  1. 数据设计

与题目二保持类似。

在类里面定义static数组储存六种算法面对随机、正序、逆序、uneven四种数据分布时运算时间，以及运算时间取对数的数值，然后再作图时取对应的数组即可。

优点是，出错几率小，改动代码较少，有利于后续扩展。

缺点是，每次运行时间长，代码冗余。

  1. 主干代码说明

生成新数据的方法：

// 1/2 的数据是 0，1/4 的数据是 1，1/8 的数据是 2 和 1/8 的数据是 3
    public static Double[] getUnevenData(int N) {
        Double[] numbers = new Double[N];
        for (int i = 0; i < (1.0 / 2) * N; i++) {
            numbers[i] = 0.0;
        }
        for (int i = (int) ((1.0 / 2) * N) ; i < (3.0 / 4) * N; i++) {
            numbers[i] = 1.0;
        }
        for (int i = (int) ((3.0 / 4) * N) ; i < (7.0 / 8) * N; i++) {
            numbers[i] = 2.0;
        }
        for (int i = (int) ((7.0 / 8) * N) ; i < N ; i++) {
            numbers[i] = 3.0;
        }
        shuffle(numbers, 0, numbers.length);
        return numbers;
    }

定义的数组，以insertion为例：

    static double[] insertion_Random_Time;
    static double[] insertion_Random_Changed_Time;
    static double[] insertion_Sorted_Time;
    static double[] insertion_Sorted_Changed_Time;
    static double[] insertion_Inversed_Time;
    static double[] insertion_Inversed_Changed_Time;
    static double[] insertion_Uneven_Time;
    static double[] insertion_Uneven_Changed_Time;

运算，以insertion为例：

        //选择排序方法
        SortAlgorithm insertion_Alg = new Insertion();
        for (int i = 0; i < dataLength.length; i++){
            insertion_Random_Time[i] = SortTest.test(insertion_Alg, GenerateData.getRandomData(dataLength[i]), 5);
            insertion_Random_Changed_Time[i] = Math.log(insertion_Random_Time[i]) / Math.log(10);//实现以10为底数

            insertion_Sorted_Time[i] = SortTest.test(insertion_Alg, GenerateData.getSortedData(dataLength[i]), 5);
            insertion_Sorted_Changed_Time[i] = Math.log(insertion_Sorted_Time[i]) / Math.log(10);//实现以10为底数

            insertion_Inversed_Time[i] = SortTest.test(insertion_Alg, GenerateData.getInversedData(dataLength[i]), 5);
            insertion_Inversed_Changed_Time[i] = Math.log(insertion_Inversed_Time[i]) / Math.log(10);//实现以10为底数

            insertion_Uneven_Time[i] = SortTest.test(insertion_Alg, GenerateData.getUnevenData(dataLength[i]), 5);
            insertion_Uneven_Changed_Time[i] = Math.log(insertion_Uneven_Time[i]) / Math.log(10);//实现以10为底数
        }
  1. 运行结果展示

不同排序算法面对uneven数据分布结构：

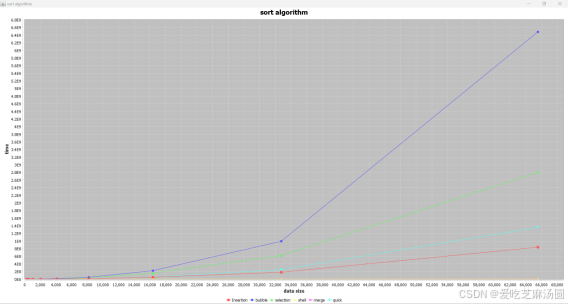
时间取指数：

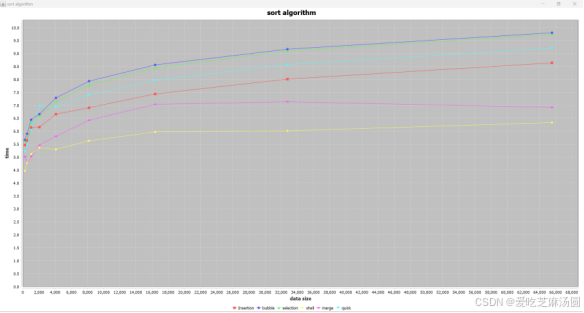
根据对算法的分析，在面对uneven数据时，采取最好策略的shell排序快于merge排序，远远快于insertion、quick、selection、bubble。

与面对随机的数据相差不大。

quick慢的原因在于没有优化。

六种排序算法面对uneven数据分布结构：

Insertion：

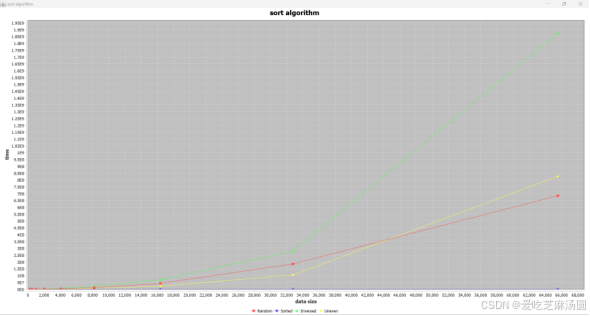
时间取指数：

对于insertion算法，输入uneven数据和输入无序数据、随机数据差距不大。

实验得到的结果与分析一致。

Bubble：

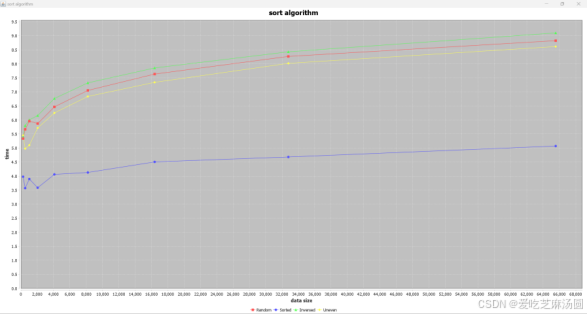
时间取指数：

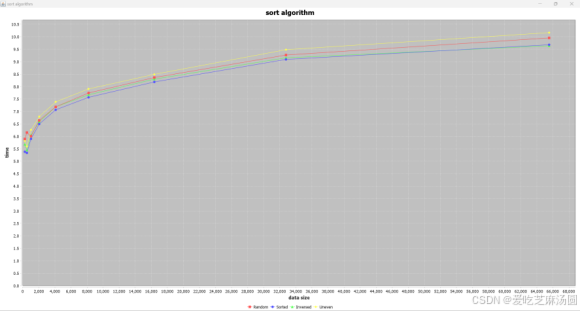
对于bubble算法，输入uneven数据和输入无序数据、随机数据差距不大，但uneven消耗时间更长效率更低。这是因为有大量的比较是没有用的。

实验得到的结果与分析一致。

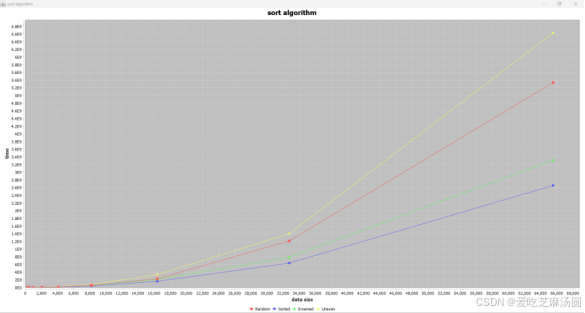
Selection：

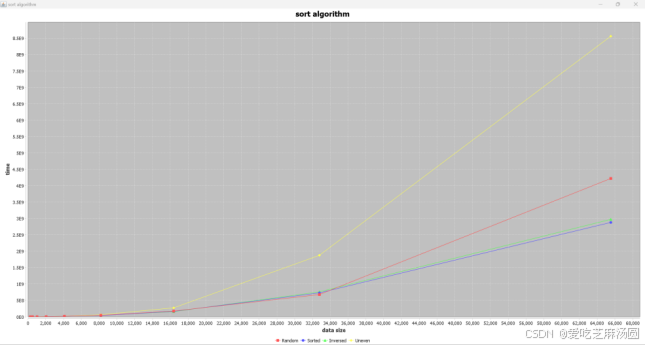
时间取指数：

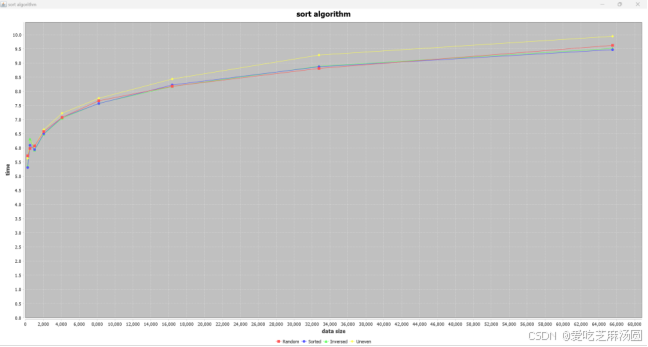
对于selection算法，输入uneven数据和输入无序数据、随机数据差距不大，但uneven消耗时间更长效率更低。这是因为有大量的比较是没有用的。

实验得到的结果与分析一致。

Shell：

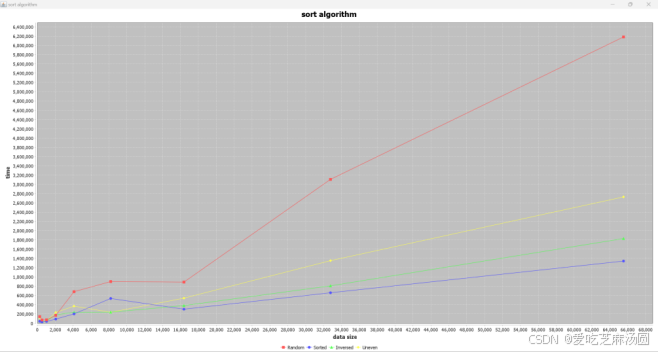
时间取指数：

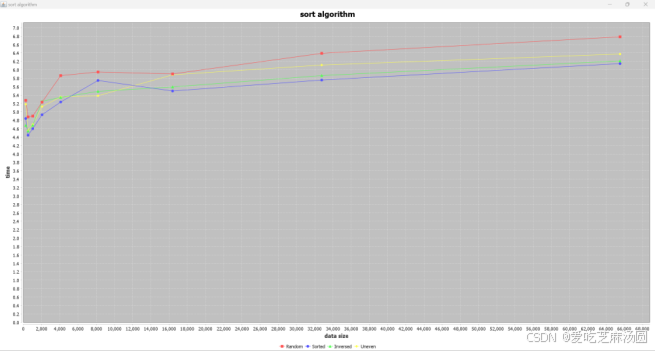
对于shell算法，输入uneven数据和输入无序数据、随机数据差距不大。

实验得到的结果与分析一致。

Merge：

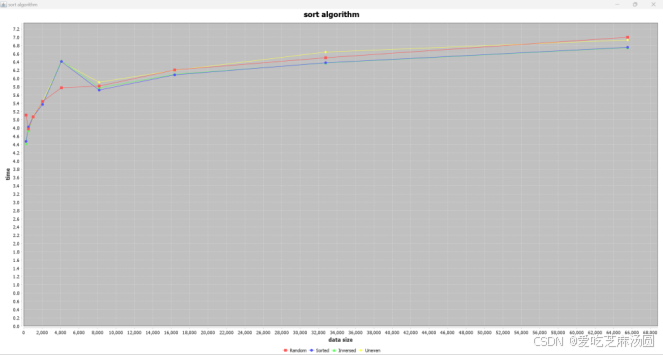
时间取指数：

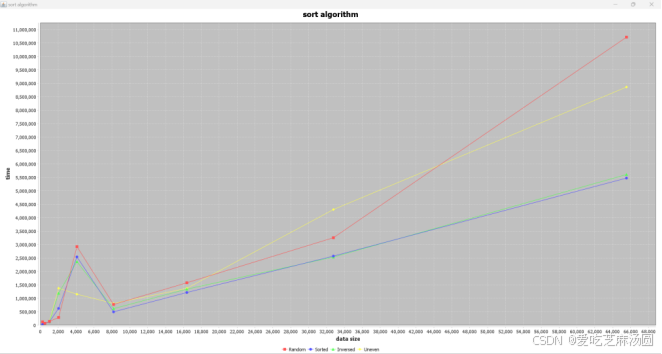
对于merge算法，输入uneven数据和输入无序数据、随机数据差距不大。

实验得到的结果与分析一致。

Quick：

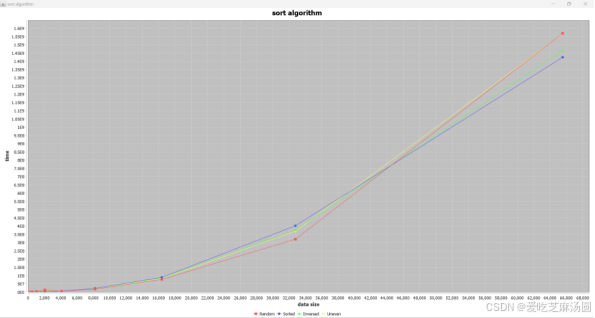
时间取指数：

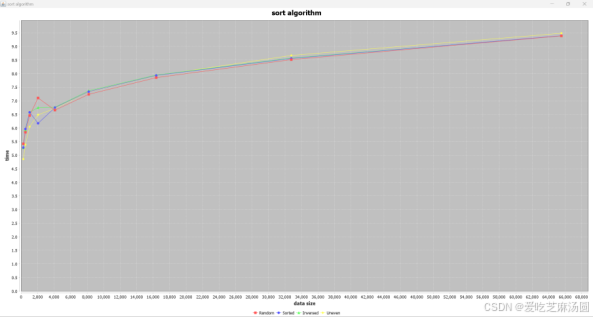
对于quick算法，输入uneven数据和输入无序数据、随机数据差距不大。

实验得到的结果与分析一致。

  1. 分析算法效率

对于random、uneven、inverted、sorted四种数据类型，不同的算法的效率有很大区别。例如，对于insertion和shell，sorted数据排序异常的快，而其他几种相对差异较小。

附录：
 

  1. 任务4

测试并绘图的类：


  1. import org.jfree.chart.ChartFactory;
  2. import org.jfree.chart.ChartPanel;
  3. import org.jfree.chart.JFreeChart;
  4. import org.jfree.chart.plot.PlotOrientation;
  5. import org.jfree.chart.plot.XYPlot;
  6. import org.jfree.chart.renderer.xy.XYLineAndShapeRenderer;
  7. import org.jfree.chart.ui.ApplicationFrame;
  8. import org.jfree.chart.ui.RectangleInsets;
  9. import org.jfree.data.xy.XYDataset;
  10. import org.jfree.data.xy.XYSeries;
  11. import org.jfree.data.xy.XYSeriesCollection;
  13. import java.awt.*;
  15. public class LineXYDemo extends ApplicationFrame {
  17.     static int[] dataLength;
  18. /*
  19.     static double[] insertion_Random_Time;
  20.     static double[] insertion_Random_Changed_Time;
  21.     static double[] insertion_Sorted_Time;
  22.     static double[] insertion_Sorted_Changed_Time;
  23.     static double[] insertion_Inversed_Time;
  24.     static double[] insertion_Inversed_Changed_Time;
  25.     static double[] insertion_Uneven_Time;
  26.     static double[] insertion_Uneven_Changed_Time;
  28.     static double[] bubble_Random_Time;
  29.     static double[] bubble_Random_Changed_Time;
  30.     static double[] bubble_Sorted_Time;
  31.     static double[] bubble_Sorted_Changed_Time;
  32.     static double[] bubble_Inversed_Time;
  33.     static double[] bubble_Inversed_Changed_Time;
  34.     static double[] bubble_Uneven_Time;
  35.     static double[] bubble_Uneven_Changed_Time;
  37.     static double[] selection_Random_Time;
  38.     static double[] selection_Random_Changed_Time;
  39.     static double[] selection_Sorted_Time;
  40.     static double[] selection_Sorted_Changed_Time;
  41.     static double[] selection_Inversed_Time;
  42.     static double[] selection_Inversed_Changed_Time;
  43.     static double[] selection_Uneven_Time;
  44.     static double[] selection_Uneven_Changed_Time;
  46.     static double[] shell_Random_Time;
  47.     static double[] shell_Random_Changed_Time;
  48.     static double[] shell_Sorted_Time;
  49.     static double[] shell_Sorted_Changed_Time;
  50.     static double[] shell_Inversed_Time;
  51.     static double[] shell_Inversed_Changed_Time;
  52.     static double[] shell_Uneven_Time;
  53.     static double[] shell_Uneven_Changed_Time;
  55.     static double[] merge_Random_Time;
  56.     static double[] merge_Random_Changed_Time;
  57.     static double[] merge_Sorted_Time;
  58.     static double[] merge_Sorted_Changed_Time;
  59.     static double[] merge_Inversed_Time;
  60.     static double[] merge_Inversed_Changed_Time;
  61.     static double[] merge_Uneven_Time;
  62.     static double[] merge_Uneven_Changed_Time;
  63. */
  64.     static double[] quick_Random_Time;
  65.     static double[] quick_Random_Changed_Time;
  66.     static double[] quick_Sorted_Time;
  67.     static double[] quick_Sorted_Changed_Time;
  68.     static double[] quick_Inversed_Time;
  69.     static double[] quick_Inversed_Changed_Time;
  70.     static double[] quick_Uneven_Time;
  71.     static double[] quick_Uneven_Changed_Time;
  74.     // 该构造方法中完成了数据集、图表对象和显示图表面板的创建工作
  75.     public LineXYDemo(String title){
  76.         super(title);
  77.         XYDataset dataset = createDataset();             // 创建记录图中坐标点的数据集
  78.         JFreeChart chart = createChart(dataset);         // 使用上一步已经创建好的数据集生成一个图表对象
  79.         ChartPanel chartPanel = new ChartPanel(chart);   // 将上一步已经创建好的图表对象放置到一个可以显示的Panel上
  80.         // 设置GUI面板Panel的显示大小
  81.         chartPanel.setPreferredSize(new Dimension(500, 270));
  82.         setContentPane(chartPanel);                      // 这是JavaGUI的步骤之一，不用过于关心，面向对象课程综合训练的视频中进行了讲解。
  83.     }
  85.     private JFreeChart createChart(XYDataset dataset) {
  86.         // 使用已经创建好的dataset生成图表对象
  87.         // JFreechart提供了多种类型的图表对象，本次实验是需要使用XYLine型的图表对象
  88.         JFreeChart chart = ChartFactory.createXYLineChart(
  89.                 "sort algorithm",      // 图表的标题
  90.                 "data size",                           // 横轴的标题名
  91.                 "time",                           // 纵轴的标题名
  92.                 dataset,                       // 图表对象中使用的数据集对象
  93.                 PlotOrientation.VERTICAL,      // 图表显示的方向
  94.                 true,                          // 是否显示图例
  95.                 false,                         // 是否需要生成tooltips
  96.                 false                          // 是否需要生成urls
  97.         );
  98.         // 下面所做的工作都是可选操作，主要是为了调整图表显示的风格
  99.         // 同学们不必在意下面的代码
  100.         // 可以将下面的代码去掉对比一下显示的不同效果
  101.         chart.setBackgroundPaint(Color.WHITE);
  102.         XYPlot plot = (XYPlot)chart.getPlot();
  103.         plot.setBackgroundPaint(Color.lightGray);
  104.         plot.setAxisOffset(new RectangleInsets(5.0, 5.0, 5.0, 6.0));
  105.         plot.setDomainGridlinePaint(Color.WHITE);
  106.         plot.setRangeGridlinePaint(Color.WHITE);
  107.         XYLineAndShapeRenderer renderer = (XYLineAndShapeRenderer) plot.getRenderer();
  108.         renderer.setDefaultShapesVisible(true);
  109.         renderer.setDefaultShapesFilled(true);
  110.         return chart;
  111.     }
  113.     private XYDataset createDataset() {
  114.         // 本样例中想要显示的是三组数据的变化图
  115.         // X数组是三组数据共同拥有的x坐标值；Y1、Y2和Y3数组分别存储了三组数据对应的y坐标值
  116.         double[][] Y = {quick_Random_Changed_Time, quick_Sorted_Changed_Time, quick_Inversed_Changed_Time,
  117.                 quick_Uneven_Changed_Time};
  118.         // jfreechart中使用XYSeries对象存储一组数据的(x,y)的序列，因为有三组数据所以创建三个XYSeries对象
  119.         XYSeries[] series = {new XYSeries("Random"), new XYSeries("Sorted"), new XYSeries("Inversed"),
  120.                 new XYSeries("Uneven")};
  121.         int N = dataLength.length;
  122.         int M = series.length;
  123.         for(int i = 0; i < M; i++)
  124.             for(int j = 0; j < N; j++)
  125.                 series[i].add(dataLength[j], Y[i][j]);
  126.         // 因为在该图表中显示的数据序列不止一组，所以在jfreechart中需要将多组数据序列存放到一个XYSeriesCollection对象中
  127.         XYSeriesCollection dataset = new XYSeriesCollection();
  128.         for(int i = 0; i < M; i++)
  129.             dataset.addSeries(series[i]);
  131.         return dataset;
  132.     }
  136.     public static void main(String[] args) {
  137.         //数据规模为：2的8次方到2的16次方
  138.         dataLength = new int[9];
  139.         for (int i = 8; i < 17; i++) {
  140.             dataLength[i - 8] = (int) Math.pow(2, i);
  141.         }
  142.         /*
  143.         //储存时间的数组
  144.         insertion_Random_Time = new double[dataLength.length];
  145.         insertion_Random_Changed_Time = new double[dataLength.length];
  146.         insertion_Sorted_Time = new double[dataLength.length];
  147.         insertion_Sorted_Changed_Time = new double[dataLength.length];
  148.         insertion_Inversed_Time = new double[dataLength.length];
  149.         insertion_Inversed_Changed_Time = new double[dataLength.length];
  150.         insertion_Uneven_Time = new double[dataLength.length];
  151.         insertion_Uneven_Changed_Time = new double[dataLength.length];
  153.         bubble_Random_Time = new double[dataLength.length];
  154.         bubble_Random_Changed_Time = new double[dataLength.length];
  155.         bubble_Sorted_Time = new double[dataLength.length];
  156.         bubble_Sorted_Changed_Time = new double[dataLength.length];
  157.         bubble_Inversed_Time = new double[dataLength.length];
  158.         bubble_Inversed_Changed_Time = new double[dataLength.length];
  159.         bubble_Uneven_Time = new double[dataLength.length];
  160.         bubble_Uneven_Changed_Time = new double[dataLength.length];
  162.         selection_Random_Time = new double[dataLength.length];
  163.         selection_Random_Changed_Time = new double[dataLength.length];
  164.         selection_Sorted_Time = new double[dataLength.length];
  165.         selection_Sorted_Changed_Time = new double[dataLength.length];
  166.         selection_Inversed_Time = new double[dataLength.length];
  167.         selection_Inversed_Changed_Time = new double[dataLength.length];
  168.         selection_Uneven_Time = new double[dataLength.length];
  169.         selection_Uneven_Changed_Time = new double[dataLength.length];
  171.         shell_Random_Time = new double[dataLength.length];
  172.         shell_Random_Changed_Time = new double[dataLength.length];
  173.         shell_Sorted_Time = new double[dataLength.length];
  174.         shell_Sorted_Changed_Time = new double[dataLength.length];
  175.         shell_Inversed_Time = new double[dataLength.length];
  176.         shell_Inversed_Changed_Time = new double[dataLength.length];
  177.         shell_Uneven_Time = new double[dataLength.length];
  178.         shell_Uneven_Changed_Time = new double[dataLength.length];
  180.         merge_Random_Time = new double[dataLength.length];
  181.         merge_Random_Changed_Time = new double[dataLength.length];
  182.         merge_Sorted_Time = new double[dataLength.length];
  183.         merge_Sorted_Changed_Time = new double[dataLength.length];
  184.         merge_Inversed_Time = new double[dataLength.length];
  185.         merge_Inversed_Changed_Time = new double[dataLength.length];
  186.         merge_Uneven_Time = new double[dataLength.length];
  187.         merge_Uneven_Changed_Time = new double[dataLength.length];
  188. */
  189.         quick_Random_Time = new double[dataLength.length];
  190.         quick_Random_Changed_Time = new double[dataLength.length];
  191.         quick_Sorted_Time = new double[dataLength.length];
  192.         quick_Sorted_Changed_Time = new double[dataLength.length];
  193.         quick_Inversed_Time = new double[dataLength.length];
  194.         quick_Inversed_Changed_Time = new double[dataLength.length];
  195.         quick_Uneven_Time = new double[dataLength.length];
  196.         quick_Uneven_Changed_Time = new double[dataLength.length];
  197. /*
  198.         //选择排序方法
  199.         SortAlgorithm insertion_Alg = new Insertion();
  200.         for (int i = 0; i < dataLength.length; i++){
  201.             insertion_Random_Time[i] = SortTest.test(insertion_Alg, GenerateData.getRandomData(dataLength[i]), 5);
  202.             insertion_Random_Changed_Time[i] = Math.log(insertion_Random_Time[i]) / Math.log(10);//实现以10为底数
  204.             insertion_Sorted_Time[i] = SortTest.test(insertion_Alg, GenerateData.getSortedData(dataLength[i]), 5);
  205.             insertion_Sorted_Changed_Time[i] = Math.log(insertion_Sorted_Time[i]) / Math.log(10);//实现以10为底数
  207.             insertion_Inversed_Time[i] = SortTest.test(insertion_Alg, GenerateData.getInversedData(dataLength[i]), 5);
  208.             insertion_Inversed_Changed_Time[i] = Math.log(insertion_Inversed_Time[i]) / Math.log(10);//实现以10为底数
  210.             insertion_Uneven_Time[i] = SortTest.test(insertion_Alg, GenerateData.getUnevenData(dataLength[i]), 5);
  211.             insertion_Uneven_Changed_Time[i] = Math.log(insertion_Uneven_Time[i]) / Math.log(10);//实现以10为底数
  214.         }
  215.         System.out.println(1);
  217.         //冒泡排序方法
  218.         SortAlgorithm bubble_Alg = new Bubble();
  219.         for (int i = 0; i < dataLength.length; i++){
  220.             bubble_Random_Time[i] = SortTest.test(bubble_Alg, GenerateData.getRandomData(dataLength[i]), 5);
  221.             bubble_Random_Changed_Time[i] = Math.log(bubble_Random_Time[i]) / Math.log(10);//实现以10为底数
  223.             bubble_Sorted_Time[i] = SortTest.test(bubble_Alg, GenerateData.getSortedData(dataLength[i]), 5);
  224.             bubble_Sorted_Changed_Time[i] = Math.log(bubble_Sorted_Time[i]) / Math.log(10);//实现以10为底数
  226.             bubble_Inversed_Time[i] = SortTest.test(bubble_Alg, GenerateData.getInversedData(dataLength[i]), 5);
  227.             bubble_Inversed_Changed_Time[i] = Math.log(bubble_Inversed_Time[i]) / Math.log(10);//实现以10为底数
  229.             bubble_Uneven_Time[i] = SortTest.test(bubble_Alg, GenerateData.getUnevenData(dataLength[i]), 5);
  230.             bubble_Uneven_Changed_Time[i] = Math.log(bubble_Uneven_Time[i]) / Math.log(10);//实现以10为底数
  232.         }
  233.         System.out.println(2);
  235.         //选择排序方法
  236.         SortAlgorithm selection_Alg = new Selection();
  237.         for (int i = 0; i < dataLength.length; i++){
  238.             selection_Random_Time[i] = SortTest.test(selection_Alg, GenerateData.getRandomData(dataLength[i]), 5);
  239.             selection_Random_Changed_Time[i] = Math.log(selection_Random_Time[i]) / Math.log(10);//实现以10为底数
  241.             selection_Sorted_Time[i] = SortTest.test(selection_Alg, GenerateData.getSortedData(dataLength[i]), 5);
  242.             selection_Sorted_Changed_Time[i] = Math.log(selection_Sorted_Time[i]) / Math.log(10);//实现以10为底数
  244.             selection_Inversed_Time[i] = SortTest.test(selection_Alg, GenerateData.getInversedData(dataLength[i]), 5);
  245.             selection_Inversed_Changed_Time[i] = Math.log(selection_Inversed_Time[i]) / Math.log(10);//实现以10为底数
  247.             selection_Uneven_Time[i] = SortTest.test(selection_Alg, GenerateData.getUnevenData(dataLength[i]), 5);
  248.             selection_Uneven_Changed_Time[i] = Math.log(selection_Uneven_Time[i]) / Math.log(10);//实现以10为底数
  250.         }
  251.         System.out.println(3);
  253.         //选择排序方法
  254.         SortAlgorithm shell_Alg = new Shell();
  255.         for (int i = 0; i < dataLength.length; i++){
  256.             shell_Random_Time[i] = SortTest.test(shell_Alg, GenerateData.getRandomData(dataLength[i]), 5);
  257.             shell_Random_Changed_Time[i] = Math.log(shell_Random_Time[i]) / Math.log(10);//实现以10为底数
  259.             shell_Sorted_Time[i] = SortTest.test(shell_Alg, GenerateData.getSortedData(dataLength[i]), 5);
  260.             shell_Sorted_Changed_Time[i] = Math.log(shell_Sorted_Time[i]) / Math.log(10);//实现以10为底数
  262.             shell_Inversed_Time[i] = SortTest.test(shell_Alg, GenerateData.getInversedData(dataLength[i]), 5);
  263.             shell_Inversed_Changed_Time[i] = Math.log(shell_Inversed_Time[i]) / Math.log(10);//实现以10为底数
  265.             shell_Uneven_Time[i] = SortTest.test(shell_Alg, GenerateData.getUnevenData(dataLength[i]), 5);
  266.             shell_Uneven_Changed_Time[i] = Math.log(shell_Uneven_Time[i]) / Math.log(10);//实现以10为底数
  270.         }
  271.         System.out.println(4);
  273.         //选择排序方法
  274.         SortAlgorithm merge_Alg = new Merge();
  275.         for (int i = 0; i < dataLength.length; i++){
  276.             merge_Random_Time[i] = SortTest.test(merge_Alg, GenerateData.getRandomData(dataLength[i]), 5);
  277.             merge_Random_Changed_Time[i] = Math.log(merge_Random_Time[i]) / Math.log(10);//实现以10为底数
  279.             merge_Sorted_Time[i] = SortTest.test(merge_Alg, GenerateData.getSortedData(dataLength[i]), 5);
  280.             merge_Sorted_Changed_Time[i] = Math.log(merge_Sorted_Time[i]) / Math.log(10);//实现以10为底数
  282.             merge_Inversed_Time[i] = SortTest.test(merge_Alg, GenerateData.getInversedData(dataLength[i]), 5);
  283.             merge_Inversed_Changed_Time[i] = Math.log(merge_Inversed_Time[i]) / Math.log(10);//实现以10为底数
  285.             merge_Uneven_Time[i] = SortTest.test(merge_Alg, GenerateData.getUnevenData(dataLength[i]), 5);
  286.             merge_Uneven_Changed_Time[i] = Math.log(merge_Uneven_Time[i]) / Math.log(10);//实现以10为底数
  289.         }
  290.         System.out.println(5);
  291. */
  292.         //选择排序方法
  293.         SortAlgorithm quick_Alg = new Quick();
  294.         for (int i = 0; i < dataLength.length; i++){
  295.             quick_Random_Time[i] = SortTest.test(quick_Alg, GenerateData.getRandomData(dataLength[i]), 5);
  296.             quick_Random_Changed_Time[i] = Math.log(quick_Random_Time[i]) / Math.log(10);//实现以10为底数
  298.             quick_Sorted_Time[i] = SortTest.test(quick_Alg, GenerateData.getSortedData(dataLength[i]), 5);
  299.             quick_Sorted_Changed_Time[i] = Math.log(quick_Sorted_Time[i]) / Math.log(10);//实现以10为底数
  301.             quick_Inversed_Time[i] = SortTest.test(quick_Alg, GenerateData.getInversedData(dataLength[i]), 5);
  302.             quick_Inversed_Changed_Time[i] = Math.log(quick_Inversed_Time[i]) / Math.log(10);//实现以10为底数
  304.             quick_Uneven_Time[i] = SortTest.test(quick_Alg, GenerateData.getUnevenData(dataLength[i]), 5);
  305.             quick_Uneven_Changed_Time[i] = Math.log(quick_Uneven_Time[i]) / Math.log(10);//实现以10为底数
  306.         }
  307.         System.out.println(6);
  309.         LineXYDemo demo = new LineXYDemo("sort algorithm");
  310.         demo.pack();
  311.         demo.setVisible(true);
  313.     }
  314. }

  1. 任务5

生成uneven的方法：

  1. public static Double[] getUnevenData(int N) {
  2.         Double[] numbers = new Double[N];
  3.         for (int i = 0; i < (1.0 / 2) * N; i++) {
  4.             numbers[i] = 0.0;
  5.         }
  6.         for (int i = (int) ((1.0 / 2) * N) ; i < (3.0 / 4) * N; i++) {
  7.             numbers[i] = 1.0;
  8.         }
  9.         for (int i = (int) ((3.0 / 4) * N) ; i < (7.0 / 8) * N; i++) {
  10.             numbers[i] = 2.0;
  11.         }
  12.         for (int i = (int) ((7.0 / 8) * N) ; i < N ; i++) {
  13.             numbers[i] = 3.0;
  14.         }
  15.         shuffle(numbers, 0, numbers.length);
  16.         return numbers;
  17.     }

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值