Chapter4 李群与李代数
李群与李代数基础
1.群是一种集合加上一种运算的代数结构,满足封闭性、结合律、幺元、逆四个条件。
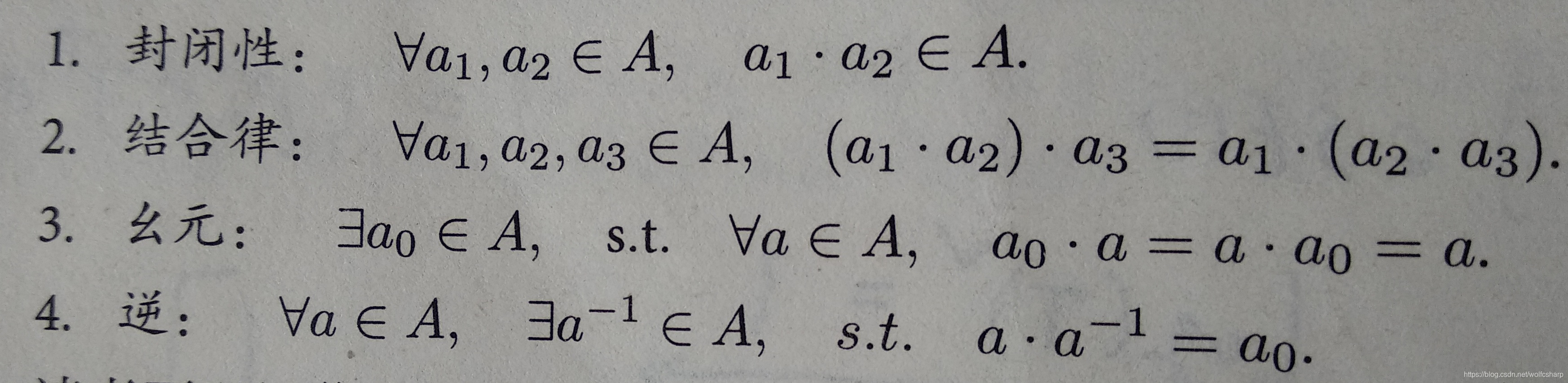
2.李群是指具有连续(光滑)性质的群
3.李代数的定义
李代数由一个集合V,一个数域F和一个二元运算[,]组成,其中二元运算被称为李括号。如果它们满足如下四条性质,则称(V,F,[,])为一个李代数:
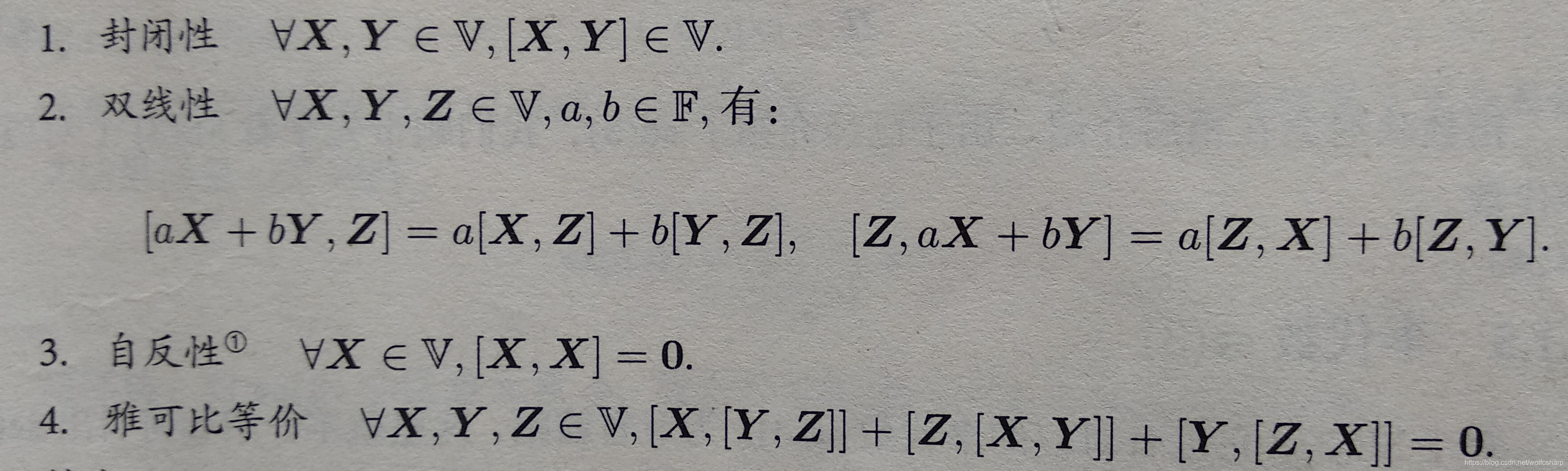
4.李代数so(3)
SO(3)对应的李代数so(3)是定义在R3空间上的向量
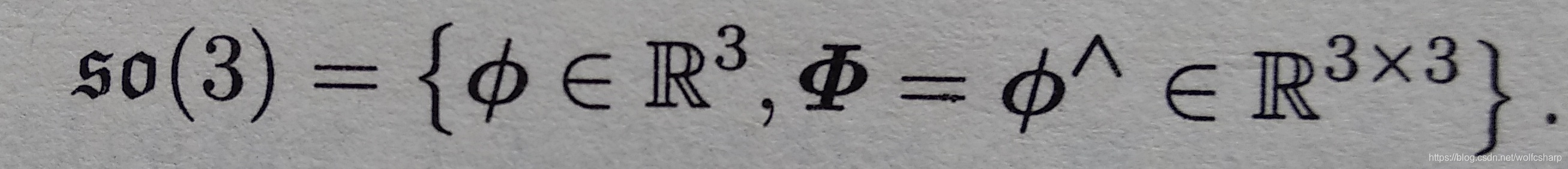
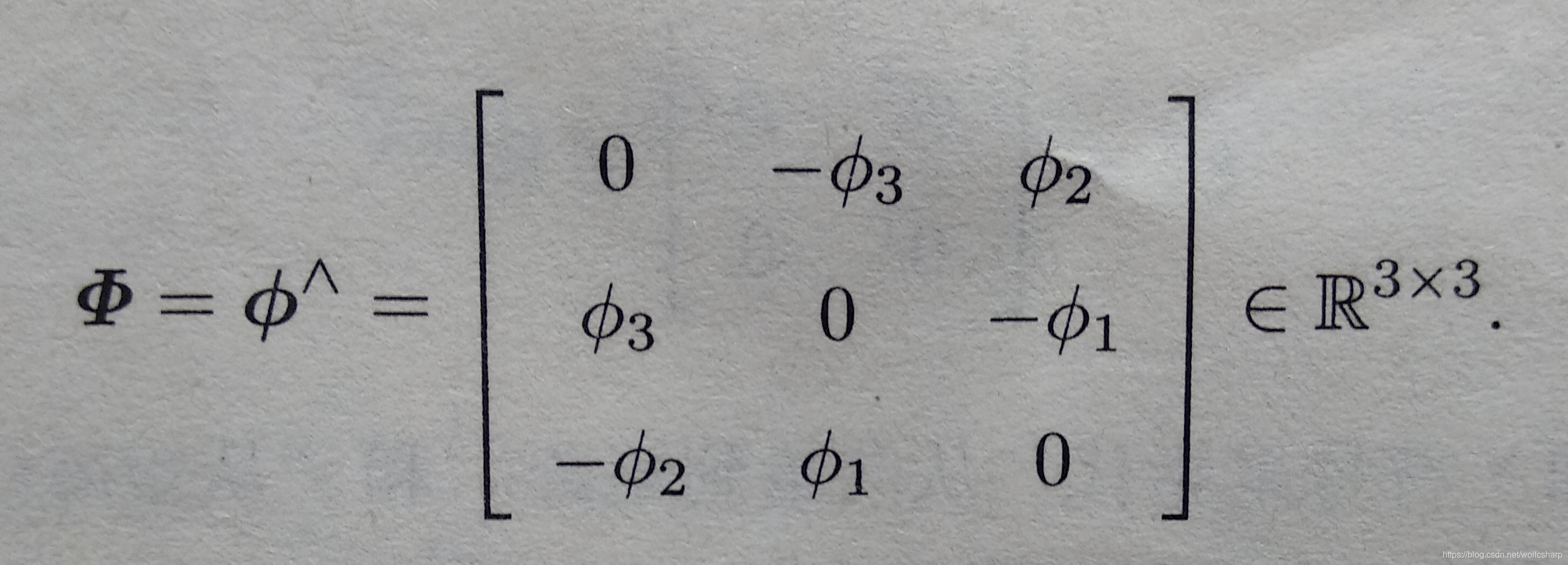
李代数so(3)的李括号为:
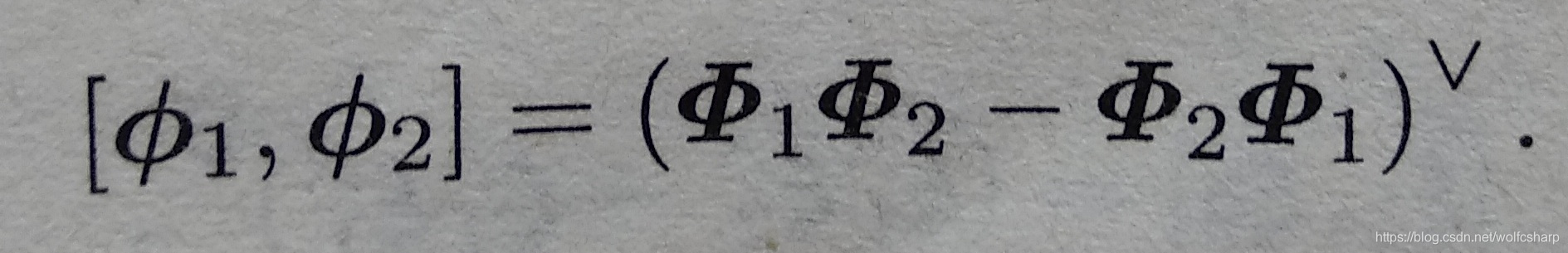
5.李代数se(3)
SE(3)对应的李代数se(3)是定义在R6空间上的向量
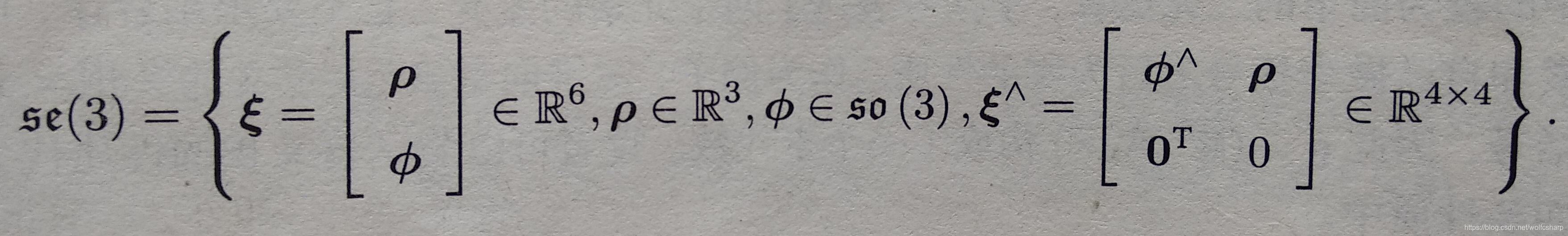
李代数se(3)的李括号为:
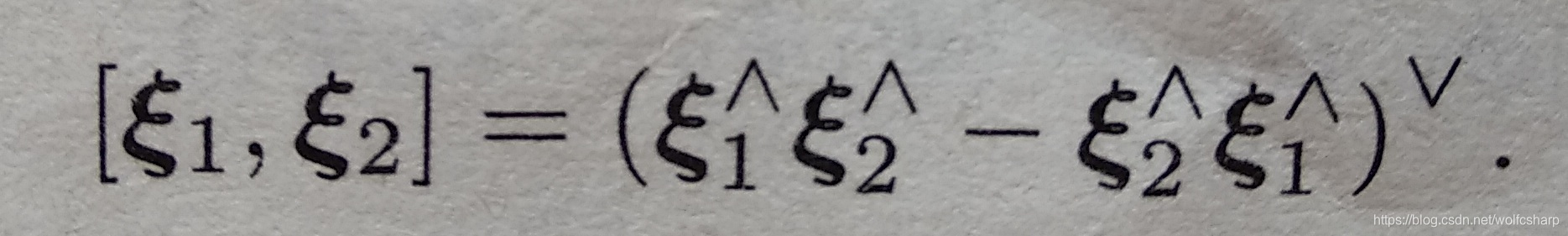
指数与对数映射
- so(3)实质上就是由所谓的旋转向量组成的空间,而指数映射即罗德里格斯公式。
推导证明如下:

- so(3)对数映射
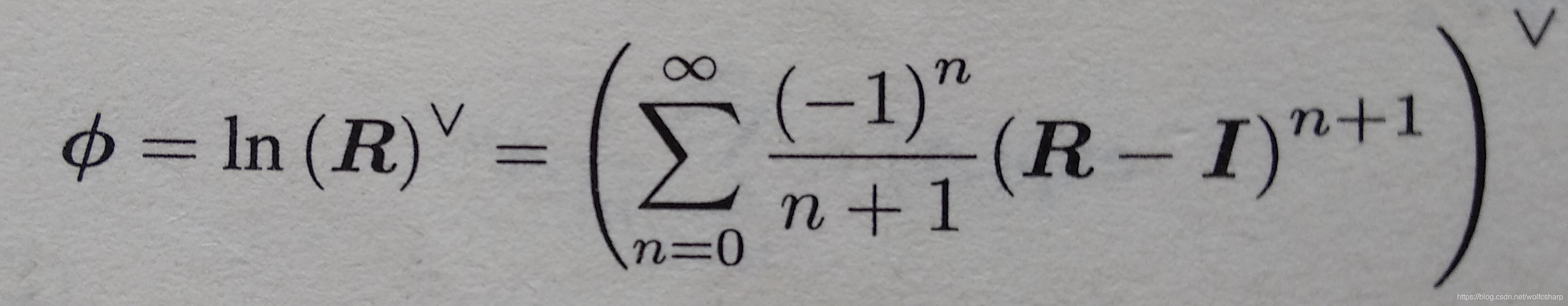
- se(3)指数映射
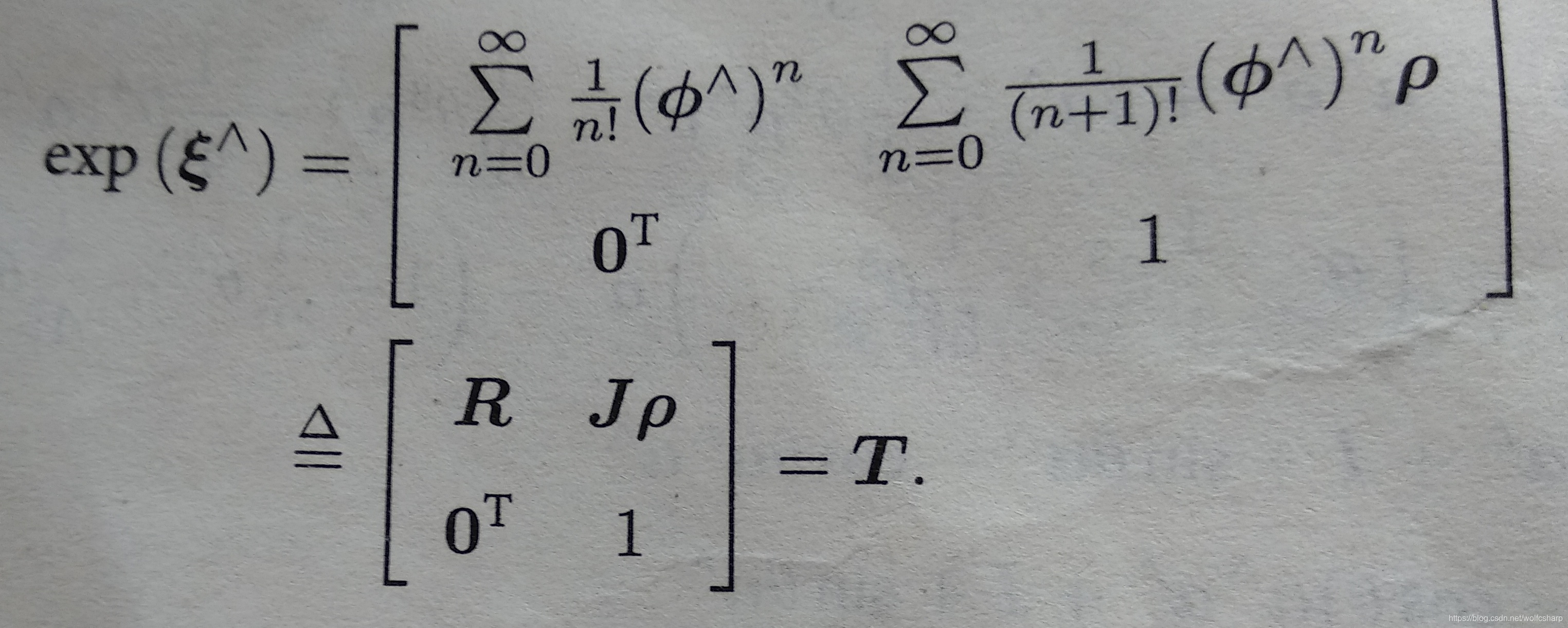
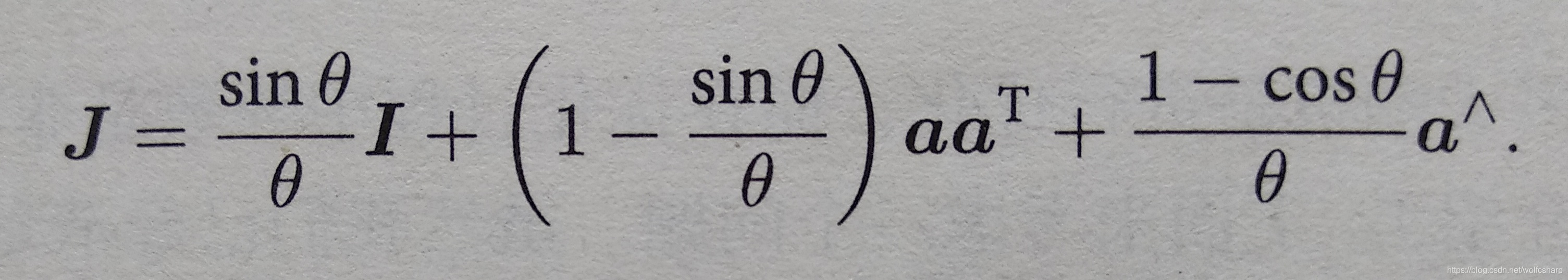
- se(3)对数映射
显然,可以先用so(3)的对数映射,得到so(3)李代数,然后根据so(3)李代数求解出J,然后根据下式求出rou
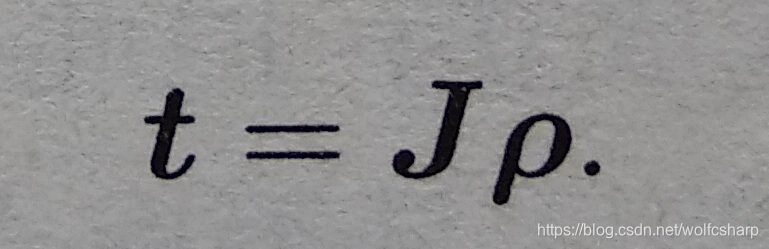
- 指数和对数映射相互转换关系
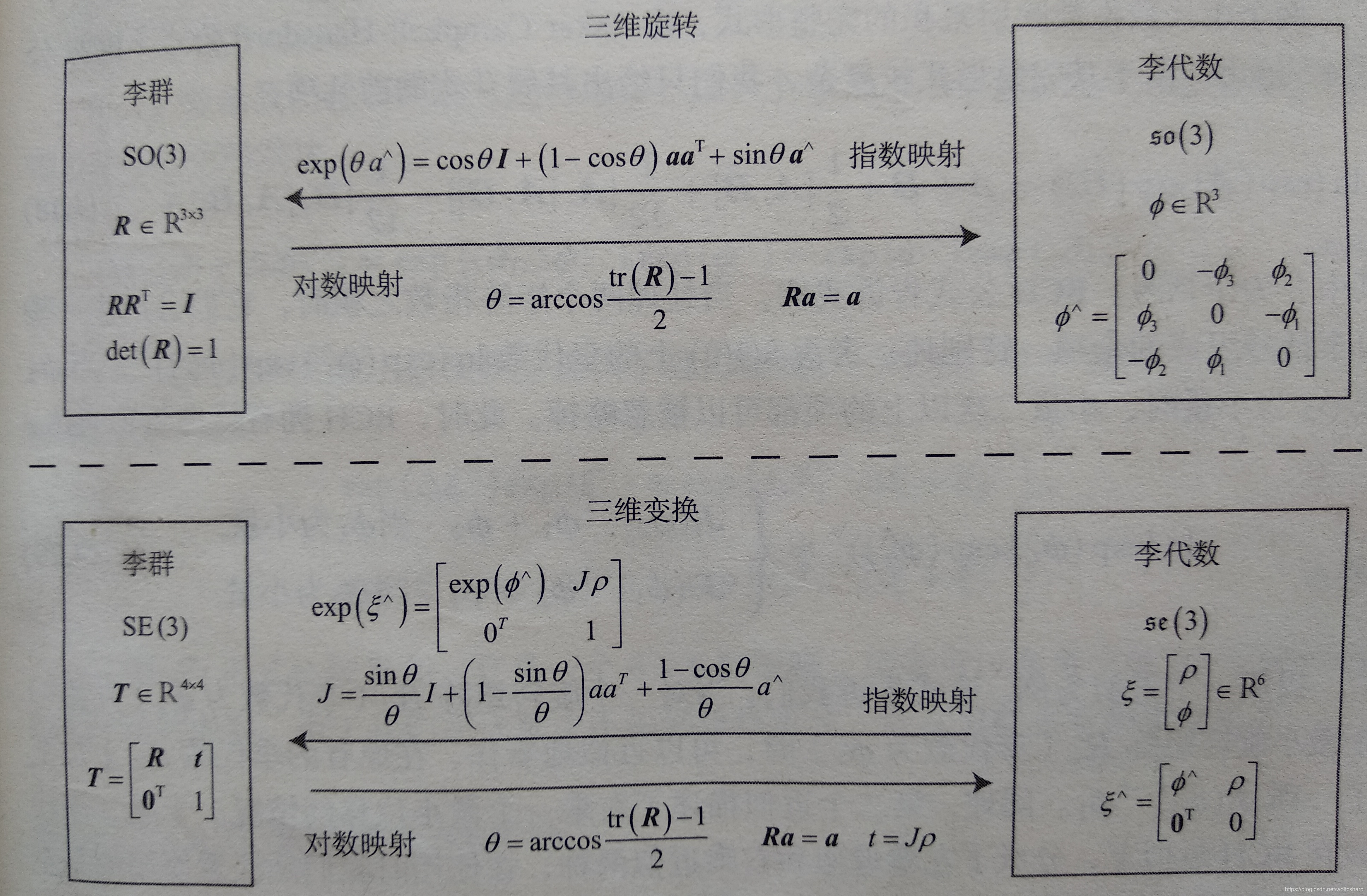
李代数求导与扰动模型
-
BCH公式与近似形式

在SE(3)上则有:
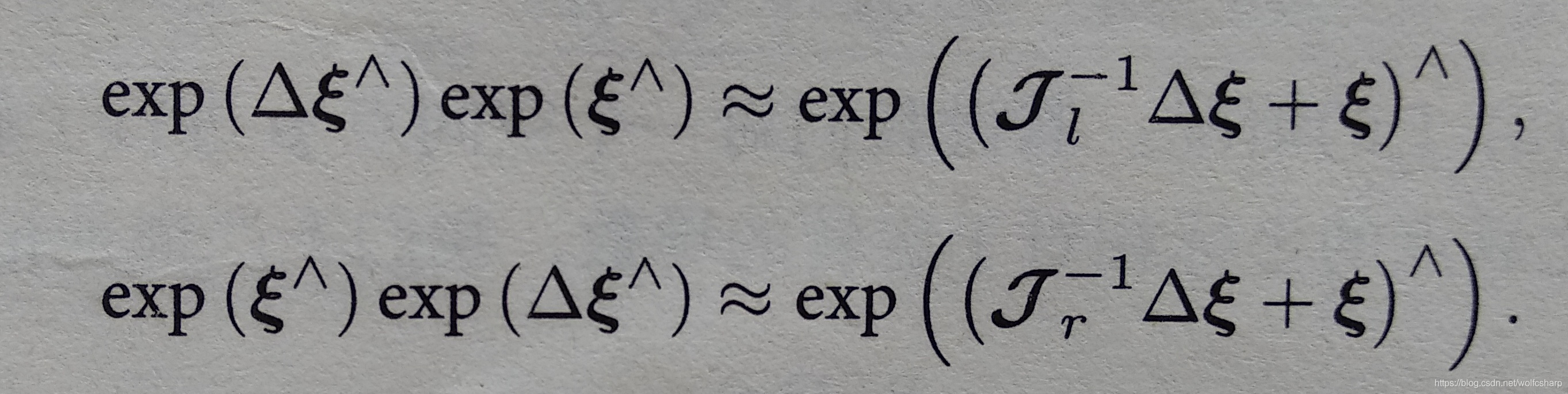
这里的雅克比是6*6的矩阵,形式比较复杂。 -
SO(3)李代数上的求导

-
左乘扰动模型求导

-
SE(3)李代数上的求导

实践:Sophus
- Sophus库支持SO(3)、SE(3)以及二维运动SO(2)、SE(2)和相似变换Sim(3)等内容。
- Sophus早期版本只提供了双精度的李群、李代数类。后续版本改写成了模板类,但增加了使用难度。书中使用的是非模板类的Sophus库
在github上获取非模板类的Sophus:
git clone https://github.com/strasdat/Sophus.git
cd Sophus
git checkout a621ff
mkdir build
cd build
cmake ..
make
sudo make install
- Sophus是一个cmake工程,编译后还需安装
- Sophus库头文件
#include "sophus/so3.h"
#include "sophus/se3.h"
- 从旋转矩阵R构造SO3
Sophus::SO3 SO3_R(R);
- 从旋转向量构造SO3
Sophus::SO3 SO3_v(0,0,M_PI/2);
- 从四元数q构造SO3
Sophus::SO3 SO3_q(q);
- 输出SO(3)时,以so(3)的形式输出
- 使用对数映射获得SO(3)的李代数so(3)
Eigen::Vector3d so3 = SO3_R.log();
- 用hat将李代数(so(3)向量)转换成反对称矩阵(SO(3)矩阵)
Sophus::SO3::hat(so3)
- 用vee将反对称矩阵(SO(3)矩阵)转换到向量(so(3)向量)
Sophus::SO3::vee(SO3_R)
- SO3左乘增量扰动模型的更新
//增量扰动模型的更新
Eigen::Vector3d update_so3(1e-4,0,0);//假设一个小的李代数扰动更新量
Sophus::SO3 SO3_updated = Sophus::SO3::exp(update_so3)*SO3_R;//左乘更新
- 由R和t构造SE(3)
Sophus::SE3 SE3_Rt(R,t);
- 由q和t构造SE(3)
Sophus::SE3 SE3_qt(q,t);
- 使用对数映射获得SE(3)的李代数se(3)
//李代数se(3)是一个六维向量,方便起见,先typedef一下
typedef Eigen::Matrix<double,6,1> Vector6d;
Vector6d se3 = SE3_Rt.log();
cout<<"se3 = "<<se3.transpose()<<endl;//观察输出,发现在Sophus中平移在前,旋转在后,与书中理论是一致的
- 用hat将李代数(se(3)向量)转换成反对称矩阵(SE(3)矩阵)
Sophus::SE3::hat(se3)
- 用vee将反对称矩阵(SE(3)矩阵)转换到向量(se(3)向量)
Sophus::SE3::vee(SE3_Rt)
- SE3左乘增量扰动模型的更新
//增量扰动模型的更新
Vector6d update_se3;//更新量
update_se3.setZero();
update_se3(0,0)=1e-4;
Sophus::SE3 SE3_updated = Sophus::SE3::exp(update_se3)*SE3_Rt;
cout<<"SE3 updated = "<<endl<<SE3_updated.matrix()<<endl;
- CMakeLists.txt中为使用sophus,需要使用find_package命令找到它
find_package(Sophus REQUIRED)
#添加Sophus头文件
include_directories(${Sophus_INCLUDE_DIRS})
#添加链接地址
target_link_libraries(useSophus ${Sophus_LIBRARIES})
完整代码:
useSophus.cpp
//2019.08.06
#include <iostream>
#include <cmath>
using namespace std;
//Eigen部分
#include <Eigen/Core>
#include <Eigen/Geometry>
//Sohpus部分
#include "sophus/so3.h"
#include "sophus/se3.h"
int main()
{
///////////////////对SO(3)的一些操作//////////////////////////
cout<<"----------------对SO(3)的一些操作---------------"<<endl;
//定义一个沿Z轴旋转90度的旋转矩阵R
Eigen::Matrix3d R = Eigen::AngleAxisd(M_PI/2, Eigen::Vector3d(0,0,1)).toRotationMatrix();//由旋转向量转换到旋转矩阵
Sophus::SO3 SO3_R(R);//Sophus::SO(3)可以直接从旋转矩阵构造
Sophus::SO3 SO3_v(0,0,M_PI/2);//Sophus::SO(3)也可以直接从旋转向量构造
//Sophus::SO(3)亦可以从四元数构造
Eigen::Quaterniond q(R);//由旋转矩阵转换到四元数
Sophus::SO3 SO3_q(q);
//以上构造方式都是等价的
//输出SO(3)时,以so(3)的形式输出
cout <<"SO(3) from matrix: "<<SO3_R<<endl;
cout <<"SO(3) from vector: "<<SO3_v<<endl;
cout <<"SO(3) from quaternion:"<<SO3_q<<endl;
//使用对数映射获得它的李代数
Eigen::Vector3d so3 = SO3_R.log();
cout<<"so3 = "<<so3.transpose()<<endl;
//用hat将向量转换成反对称矩阵
cout<<"so3 hat = "<<endl<<Sophus::SO3::hat(so3).transpose()<<endl;
//相对的,用vee将反对称矩阵转换到向量
cout<<"so3 hat vee = "<<Sophus::SO3::vee(Sophus::SO3::hat(so3)).transpose()<<endl;
//增量扰动模型的更新
Eigen::Vector3d update_so3(1e-4,0,0);//假设一个小的李代数更新量
Sophus::SO3 SO3_updated = Sophus::SO3::exp(update_so3)*SO3_R;//左乘更新
cout<<"SO3 updated = "<<SO3_updated<<endl;
///////////////////下面是对SE(3)的操作//////////////////////
cout<<"----------------对SE(3)的一些操作---------------"<<endl;
Eigen::Vector3d t(1,0,0);//定义平移向量t,沿X轴平移1
Sophus::SE3 SE3_Rt(R,t);//由R和t构造SE(3)
Sophus::SE3 SE3_qt(q,t);//由q和t构造SE(3)
cout<<"SE3 from R,t="<<endl<<SE3_Rt<<endl;
cout<<"SE3 from q,t="<<endl<<SE3_qt<<endl;
//李代数se(3)是一个六维向量,方便起见,先typedef一下
typedef Eigen::Matrix<double,6,1> Vector6d;
Vector6d se3 = SE3_Rt.log();
cout<<"se3 = "<<se3.transpose()<<endl;//观察输出,发现在Sophus中平移在前,旋转在后,与书中理论是一致的
//hat运算
cout<<"se3 hat = "<<endl<<Sophus::SE3::hat(se3).transpose()<<endl;
//vee运算
cout<<"SE3 vee = "<<endl<<Sophus::SE3::vee(Sophus::SE3::hat(se3)).transpose()<<endl;
//增量扰动模型的更新
Vector6d update_se3;//更新量
update_se3.setZero();
update_se3(0,0)=1e-4;
Sophus::SE3 SE3_updated = Sophus::SE3::exp(update_se3)*SE3_Rt;
cout<<"SE3 updated = "<<endl<<SE3_updated.matrix()<<endl;
return 0;
}
CMakeLists.txt
#2019.08.06
#添加Eigen的头文件
include_directories("/usr/include/eigen3")
#为使用sophus,需要使用find_package命令找到它
find_package(Sophus REQUIRED)
include_directories(${Sophus_INCLUDE_DIRS})
#添加一个可执行程序
add_executable( useSophus useSophus.cpp )
#添加链接地址
target_link_libraries(useSophus ${Sophus_LIBRARIES})
运行结果:






 本文深入探讨了李群与李代数的基础概念,详细介绍了SO(3)和SE(3)李群及其对应的李代数so(3)和se(3),并利用Sophus库进行实践操作,包括指数与对数映射、左乘扰动模型的更新等关键操作。
本文深入探讨了李群与李代数的基础概念,详细介绍了SO(3)和SE(3)李群及其对应的李代数so(3)和se(3),并利用Sophus库进行实践操作,包括指数与对数映射、左乘扰动模型的更新等关键操作。
















 692
692

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








