战争策略优化算法，MATLAB代码免费获取

注：该算法已按照智能优化算法APP标准格式进行整改，可直接集成到APP中，方便大家与自己的算法进行对比。

战争策略优化算法（War Strategy Optimization Algorithm，WSO)是一种基于古代战争策略的元启发式优化算法。战争战略优化(WSO)是基于军队在战争中的战略运动，将战争策略建模为一个优化过程，每个士兵都动态地向最优值移动。该算法对两种流行的战争策略——进攻和防御策略进行建模，士兵在战场上的位置根据实施的战略而更新。为了提高算法的收敛性和鲁棒性，引入了一种新的权值更新机制和弱士兵重新定位策略。

该成果于2022年发表在计算机领域三区SCI期刊“IEEE Access”上，目前被引232次。WSO实现了探索阶段和开发阶段的良好平衡。

1.算法原理

在每次迭代中，所有士兵都有相同的概率成为国王或指挥官，这取决于他们的战斗强度(适应度值)。国王和指挥官都是战场上的领袖。国王和指挥官在战场上的行动将引导其余的士兵。国王或指挥官都有可能面临对手士兵的激烈竞争，后者有足够的力量诱捕首领。为了避免这种情况，士兵在战争中不仅要根据国王或指挥官的位置来指导，还要根据他们的联合移动战术来指导。

（1）进攻策略

我们模拟了两种战争策略。在第一种情况下，每个士兵根据国王和指挥官的位置更新自己的位置。攻击模型的这种更新机制如图所示。国王占据了有利地位，可以对反对派发动大规模进攻。因此，攻击力或体能最强的士兵被视为国王。在战争开始时，所有士兵的军衔和体重都是一样的。如果士兵成功地执行了战略，他的军衔就会上升。然而，随着战争的进展，所有士兵的等级和权重将根据战略的成功而更新。随着战争接近尾声，国王、军队指挥官和士兵的位置在接近目标时保持非常接近。

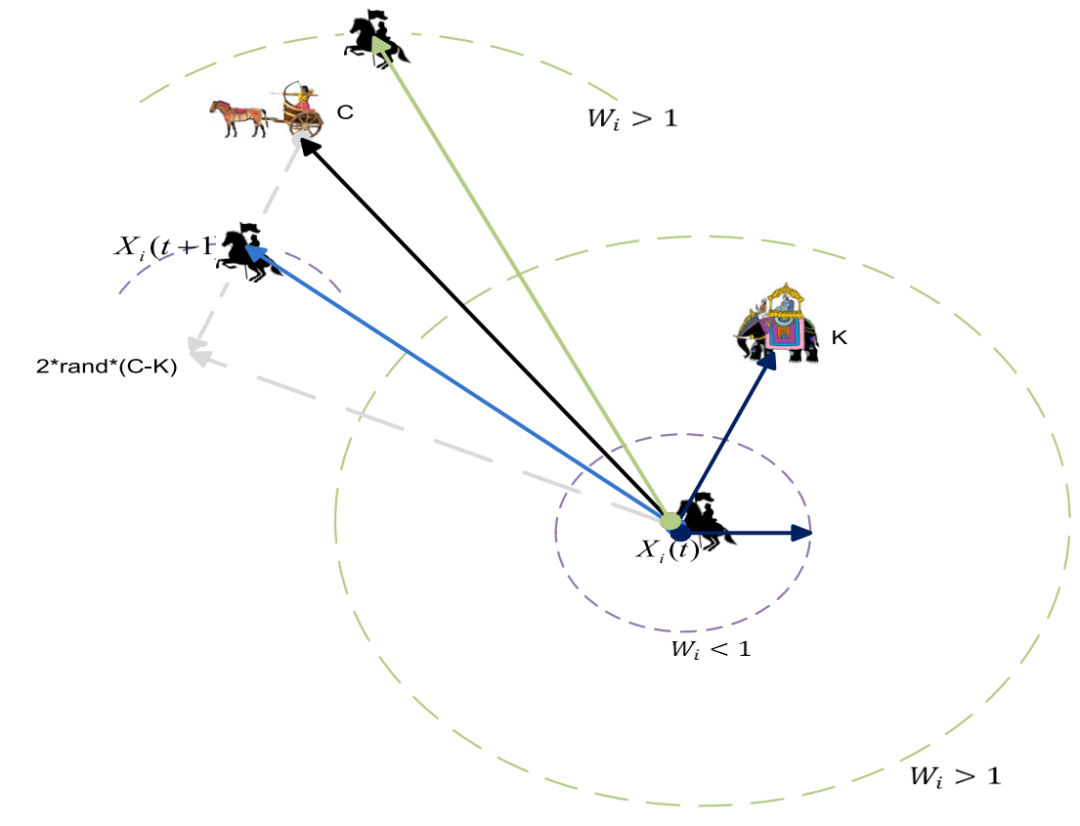
式中，Xi(t+1)为新位置，Xi为之前的C位置，为指挥官位置，K为国王位置，Wi为权重。

图中士兵周围的彩色圆圈表示基于国王位置的Wi×k−Xi(t)的轨迹点。如果Wi>1，则Wi×k−Xi(t)的位置在国王位置之外，因此更新后的士兵位置在指挥官位置之外。如果Wi<1，则Wi×k−Xi(t)的位置在国王位置和士兵当前位置之间。与之前的情况相比，更新后的士兵位置更近。如果Wi趋向于零，那么士兵的更新位置将非常接近指挥官的位置，这代表了战争的最后阶段。

每个搜索代理的位置更新取决于国王，指挥官和每个士兵的军衔的位置的相互作用。每个士兵的军衔取决于他在战场上的成功历史，这将随后影响加权因子Wi。每个士兵的等级反映了士兵（搜索代理）与目标（适应度值）的接近程度。可以注意到，在其他竞争算法如GWO、WOA、GSA、PSO中的权重因子将线性变化，而在当前提出的WSO算法中，权重（Wi）作为因子α呈指数变化。

如果新位置（Fn）的攻击力（适应性）小于前一位置（Fp），则士兵采取前一位置。

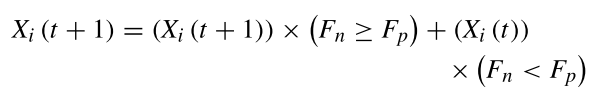
果该士兵更新位置成功，则该士兵的军衔Ri将被升级

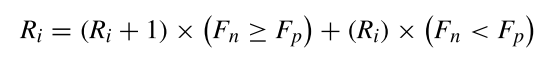
根据排名，新权重计算如下：

（2）国防战略

第二个战略位置更新是基于国王，军队首领和随机士兵的位置。而排名和权重更新保持不变。

与前一个策略相比，这个战争策略探索了更多的搜索空间，因为它涉及到随机士兵的位置。对于较大的Wi值，士兵会采取较大的步骤并更新其位置。对于小的值，Wi士兵在更新位置时采取小步骤。

（3）替换/重新安置弱兵

对于每一次迭代，找出适应性最差的弱士兵。WSO已经测试了多种替代方法。一种最简单的方法是用下式中的随机士兵替换弱士兵。

第二种方法是将弱兵迁移到更靠近战场全军中位数的位置，如公式所示。这种方法改善了算法的收敛性。

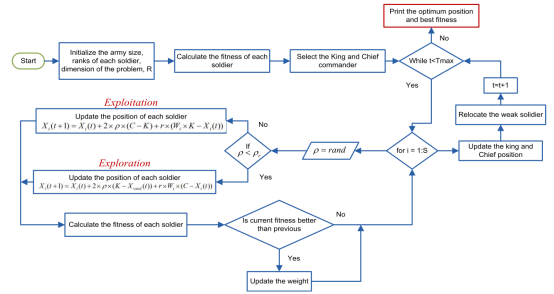
战争策略优化算法流程图如图所示。分配给每个士兵的权重是自适应的，并且会随着迭代而变化。随着战争接近尾声，士兵们为了达到目标而小步前进，每小步的重量都在变化。因为策略是随机选择的，士兵们朝随机的方向移动，而不是精确地跟随国王。这提高了算法的搜索能力。目标区域由军队在战争结束时确定(突出的搜索空间)。军队包围目标，国王和指挥官也非常接近目标。

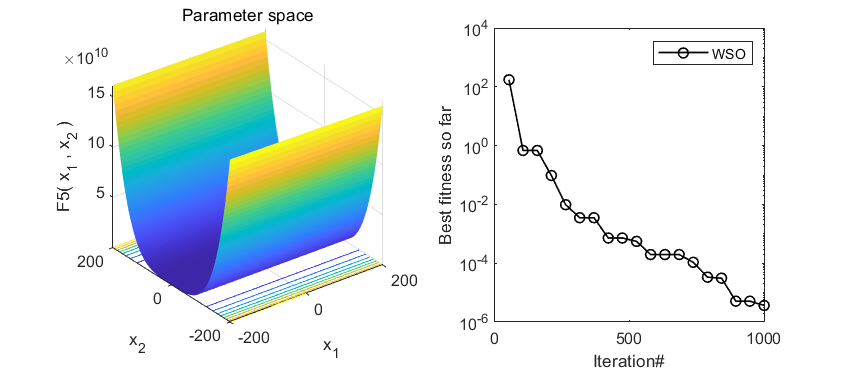
2.结果展示

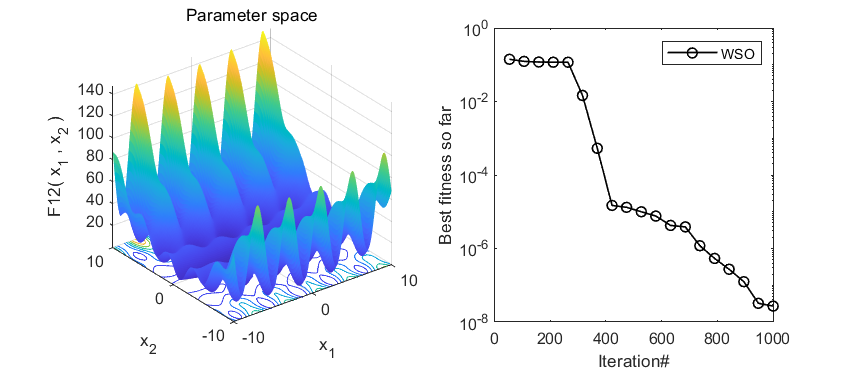
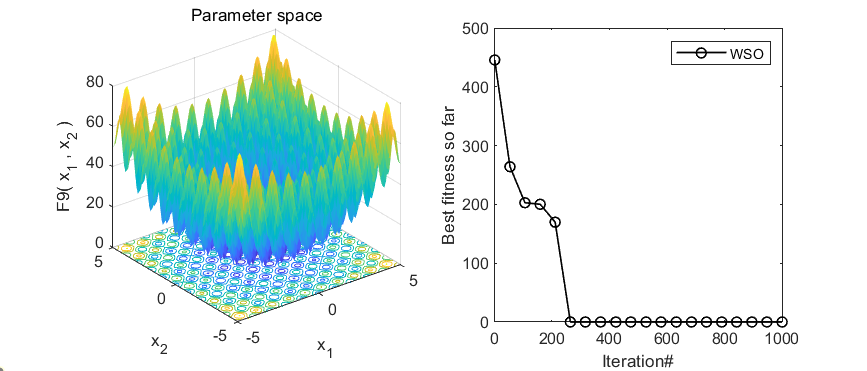
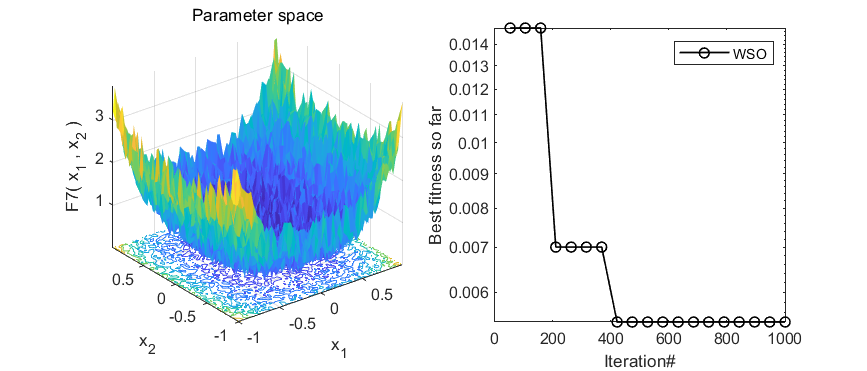
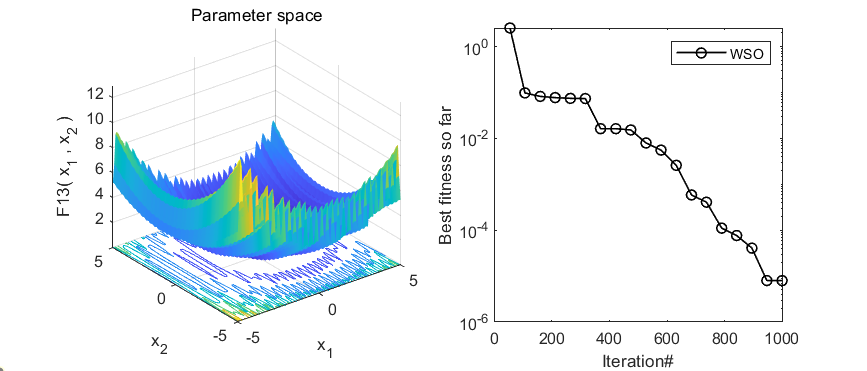
3.MATLAB核心代码

% 战争策略优化算法（War Strategy Optimization Algorithm，WSO)
function [King_fit,King,Convergence_curve]=WSO(Soldiers_no,Max_iter,lb,ub,dim,fobj)
% global W1 fitness_history position_history  Trajectories l
% fitness_history=zeros(Soldiers_no,Max_iter);
% position_history=zeros(Soldiers_no,Max_iter,dim);
% initialize alpha, beta, and delta_pos

King=zeros(1,dim);
King_fit=inf;
Positions=initialization(Soldiers_no,dim,ub,lb);
pop_size=size(Positions,1);Convergence_curve=zeros(1,Max_iter);

Positions_new=zeros(size(Positions));
fitness_old=inf*ones(1,pop_size);
fitness_new=inf*ones(1,pop_size);l=0;% Loop counter
W1=2*ones(1,pop_size);
Wg=zeros(1,pop_size);

Trajectories=zeros(Soldiers_no,Max_iter);
% Main loop
R=0.1; % Select suitable value based on the application
for  j=1:size(Positions,1)
         fitness=fobj(Positions(j,:));
         fitness_old(j)=fitness;
        if fitness<King_fit
            King_fit=fitness;
            King=Positions(j,:);
        end
end
 
while l<Max_iter
%     l
[~,tindex]=sort(fitness_old);
Co=Positions(tindex(2),:);
  
  iter =l;
   com=randperm(pop_size);  
    for i=1:pop_size
        RR=rand;
        if RR<R

             D_V(i,:)=2*RR*(King-Positions(com(i),:))+1*W1(i)*rand*(Co-Positions(i,:)); 
        else
            D_V(i,:)=2*RR*(Co-King)+1*rand*(W1(i)*King-Positions(i,:)); 
        end
            

            Positions_new(i,:)=Positions(i,:)+D_V(i,:);
            Flag4ub=Positions_new(i,:)>ub;
            Flag4lb=Positions_new(i,:)<lb;
            Positions_new(i,:)=(Positions_new(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;  
            fitness=fobj(Positions_new(i,:));
            fitness_new(i) = fitness;
        if fitness<King_fit
            King_fit=fitness;
            King=Positions_new(i,:);
        end
%         Co
        if fitness<fitness_old(i)
            Positions(i,:)=Positions_new(i,:);
            fitness_old(i)=fitness;
            Wg(i)=Wg(i)+1;
            W1(i)=1*W1(i)*(1-Wg(i)/Max_iter)^2;
        end
%         [~,tindex1]=max(fitness_old);
%         Positions(tindex1,:)=lb+rand*(ub-lb);
%         W1(tindex1)=0.5;
    end
    if l<1000
        [~,tindex1]=max(fitness_old);
        Positions(tindex1,:)=lb+rand*(ub-lb);
%         Positions(tindex1,:)=(1-randn(1))*(King-median(Positions(1:pop_size,:)))+Positions(tindex1,:);
%         Positions(tindex1,:)=rand*King;
%         W1(tindex1)=0.5;
    end
    l=l+1;    
    Convergence_curve(l)=King_fit;
end

4.参考文献

[1]Ayyarao T S L V, Ramakrishna N S S, Elavarasan R M, et al. War strategy optimization algorithm: a new effective metaheuristic algorithm for global optimization[J]. IEEE Access, 2022, 10: 25073-25105.

完整代码获取

后台回复关键词：

TGDM817