常用智能优化算法改进策略---变异篇（五种变异策略）可用于改进所有智能算法，让小白也会改进智能算法。...

原创已于 2024-02-01 10:21:21 修改 · 1.1w 阅读

139 ·

CC 4.0 BY-SA版权

文章标签：

#算法

于 2023-10-13 14:00:34 首次发布

本期文章将讲述常用智能优化算法改进策略---变异篇，一共包含五种常见的变异策略：

高斯变异，t分布扰动变异，自适应t分布扰动变异，柯西变异，差分变异。

五种策略可以方便移植到其他智能算法的改进中！

为了方便大家对变异策略的深入了解，作者将在简单易懂的粒子群算法教大家如何运用这五种策略，今后也方便大家移植到别的智能算法中。

高斯变异：

高斯函数如下：

带入粒子群算法中如下：

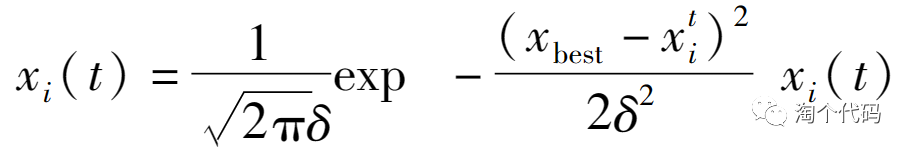
t分布扰动变异：

带入粒子群算法中如下：

自适应t分布扰动变异；

对C_Iter进行自适应变化，可以在算法前期进行全局搜索，在后期进行局部搜索，从而达到收敛。

freen = exp(4.*(l/iter).^2);

然后再带入此式当中：

柯西变异：

柯西概率密度函数如下：

带入粒子群算法中：

xnewbest=xbest+xbest×Cauchy(0,1)

随机差分变异：

Xα是全局最优粒子，X‘(t)是随机粒子，r是一个[0,1]的随机数。

结果展示

在CEC2005函数集进行展示，设置迭代次数1000次，种群个数100个。

其中PSO为原始粒子群，GPSO是高斯变异的粒子群，t-PSO是t分布变异的粒子群，self_adaption_t_PSO是自适应t分布变异的粒子群，CPSO是柯西变异的粒子群，DE-PSO是差分变异的粒子群。

注意！本程序代码只是为了教大家如何使用这几种变异策略，如果看到改进后的算法没有原始算法效果好，请不要见怪！

这几种策略并非说用到某种算法上就一定会效果好，关键要看算法本身的原理公式适不适合！要分析其原理并不断进行尝试！

代码展示

%
clear
clc
close all
number='F'; %选定优化函数，自行替换:F1~F23
[lb,ub,dim,fobj]=CEC2005(number);  % [lb,ub,D,y]：下界、上界、维度、目标函数表达式
SearchAgents=100;                      % population members 
Max_iterations=1000;                  % maximum number of iteration


%% 调用PSO算法
[fMin , bestX, PSO_Convergence_curve ] = PSO(SearchAgents, Max_iterations,lb,ub,dim,fobj);
display(['The best optimal value of the objective funciton found by PSO  for ' [num2str(number)],'  is : ', num2str(fMin)]);
fprintf ('Best solution obtained by PSO: %s\n', num2str(bestX,'%e  '));


%% 调用高斯变异的PSO
[Best_score,Best_pos,GPSO_curve]=GPSO(SearchAgents,Max_iterations,lb,ub,dim,fobj);  % Calculating the solution of the given problem using GPSO
display(['The best optimal value of the objective funciton found by GPSO  for ' [num2str(number)],'  is : ', num2str(Best_score)]);
fprintf ('Best solution obtained by GPSO: %s\n', num2str(Best_pos,'%e  '));


%% 调用t分布扰动的PSO算法
[Alpha_score,Alpha_pos,t_PSO_Convergence_curve]=t_PSO(SearchAgents,Max_iterations,lb,ub,dim,fobj);
display(['The best optimal value of the objective funciton found by t_PSO  for ' [num2str(number)],'  is : ', num2str(Alpha_score)]);
fprintf ('Best solution obtained by t_PSO: %s\n', num2str(Alpha_pos,'%e  '));


%% 调用自适应t分布扰动的PSO算法
[Alpha_score,Alpha_pos,self_adaption_t_PSO_Convergence_curve]=self_adaption_t_PSO(SearchAgents,Max_iterations,lb,ub,dim,fobj);
display(['The best optimal value of the objective funciton found by self_adaption_t_PSO  for ' [num2str(number)],'  is : ', num2str(Alpha_score)]);
fprintf ('Best solution obtained by self_adaption_t_PSO: %s\n', num2str(Alpha_pos,'%e  '));
%% 调用柯西变异扰动的PSO算法
[Alpha_score,Alpha_pos,CPSO_Convergence_curve]=CPSO(SearchAgents,Max_iterations,lb,ub,dim,fobj);
display(['The best optimal value of the objective funciton found by CPSO  for ' [num2str(number)],'  is : ', num2str(Alpha_score)]);
fprintf ('Best solution obtained by CPSO: %s\n', num2str(Alpha_pos,'%e  '));
%% 调用差分变异扰动的PSO算法
[Alpha_score,Alpha_pos,DE_PSO_Convergence_curve]=DE_PSO(SearchAgents,Max_iterations,lb,ub,dim,fobj);
display(['The best optimal value of the objective funciton found by DE_PSO  for ' [num2str(number)],'  is : ', num2str(Alpha_score)]);
fprintf ('Best solution obtained by DE_PSO: %s\n', num2str(Alpha_pos,'%e  '));
 %% Figure
figure1 = figure('Color',[1 1 1]);
G1=subplot(1,2,1,'Parent',figure1);
func_plot(number)
title(number)
xlabel('x')
ylabel('y')
zlabel('z')
subplot(1,2,2)
G2=subplot(1,2,2,'Parent',figure1);
CNT=20;
k=round(linspace(1,Max_iterations,CNT)); %随机选CNT个点
% 注意：如果收敛曲线画出来的点很少，随机点很稀疏，说明点取少了，这时应增加取点的数量，100、200、300等，逐渐增加
% 相反，如果收敛曲线上的随机点非常密集，说明点取多了，此时要减少取点数量
iter=1:1:Max_iterations;
if ~strcmp(number,'F16')&&~strcmp(number,'F9')&&~strcmp(number,'F11')  %这里是因为这几个函数收敛太快，不适用于semilogy，直接plot
    semilogy(iter(k),PSO_Convergence_curve(k),'b-^','linewidth',1);
    hold on
    semilogy(iter(k),GPSO_curve(k),'m-*','linewidth',1);
    hold on
    semilogy(iter(k),t_PSO_Convergence_curve(k),'r->','linewidth',1);
    hold on
    semilogy(iter(k),self_adaption_t_PSO_Convergence_curve(k),'k-p','linewidth',1);
    hold on
    semilogy(iter(k),CPSO_Convergence_curve(k),'g-v','linewidth',1);
    hold on
    semilogy(iter(k),DE_PSO_Convergence_curve(k),'y-+','linewidth',1);


else
    plot(iter(k),PSO_Convergence_curve(k),'b-^','linewidth',1);
    hold on
    plot(iter(k),GPSO_curve(k),'m-*','linewidth',1);
    hold on
    plot(iter(k),t_PSO_Convergence_curve(k),'r->','linewidth',1);
    hold on
    plot(iter(k),self_adaption_t_PSO_Convergence_curve(k),'k-p','linewidth',1);
    hold on
    plot(iter(k),CPSO_Convergence_curve(k),'g-v','linewidth',1);
    hold on
    plot(iter(k),DE_PSO_Convergence_curve(k),'y-+','linewidth',1);
end
grid on;
title('收敛曲线')
xlabel('迭代次数');
ylabel('适应度值');
box on
legend('PSO','GPSO','t-PSO','self-adaption_t-PSO','CPSO','DE-PSO')
set (gcf,'position', [300,300,800,330])

代码目录