用SPSS进行多变量数据分析
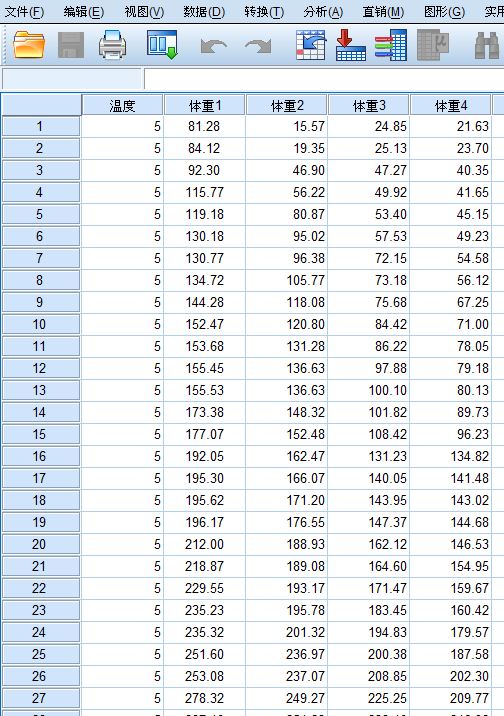
1.将所给的数据输入SPSS 22.0中文版。分别设置变量为温度,体重1、2、3、4;体重,温度5、10、15、20、30。
2.用SPSS进行作图(过程略)。
3.对数据进行多因素变量分析,具体操作如下:
(1)以体重组和温度5、10、15、20、30作为变量,在菜单里选择分析->比较平均值->单因素ANOVA,将体重组选入“因子”,将温度5、10、15、20、30选入“因变量列表”,在“事后多重比较”中选中Tukey-B(视情况选择其他),分别修改显著性水平为0.05、0.01,点击“选项”,勾选“描述性”,然后点击确定,得到输出结果,把结果导出到Excel里。
(2)以温度和体重组1、2、3、4作为变量,再次重复上述步骤,其中将温度选入“因子”,将体重组1、2、3、4选入“因变量列表”,其余操作步骤相同。
(3)根据SPSS导出的数据,处理结果如下:
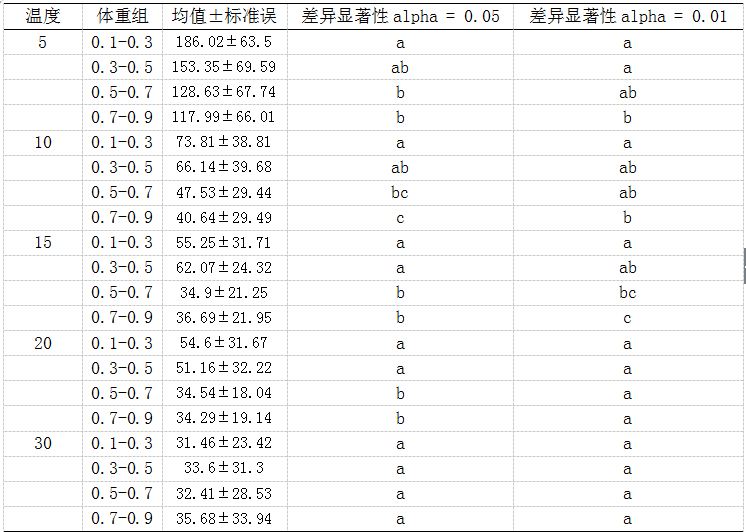
表1 同一温度下,不同体重组之间显著性分析结果
Table 1 The significant results of different weight at the same temperature
从表1可以得出结论:
1.在alpha = 0.05水平上,在5℃时,体重组1和体重组3、4有明显差异;在10℃时,体重组1和3、4之间有明显差异,体重组2和4之间有明显差异;在15℃和20℃时,体重组1、2和3、4之间有明显差异;在30℃时,各体重组之间无明显差异。
2.在alpha = 0.01水平上,在5℃时,体重组1、2和4之间有明显差异;在10℃时,体重组1和4之间有明显差异;在15℃时,体重组1和3、4,2和4之间有明显差异;在20℃和30℃时,各体重组之间无明显差异。
注:有不同字母即代表有明显差异。
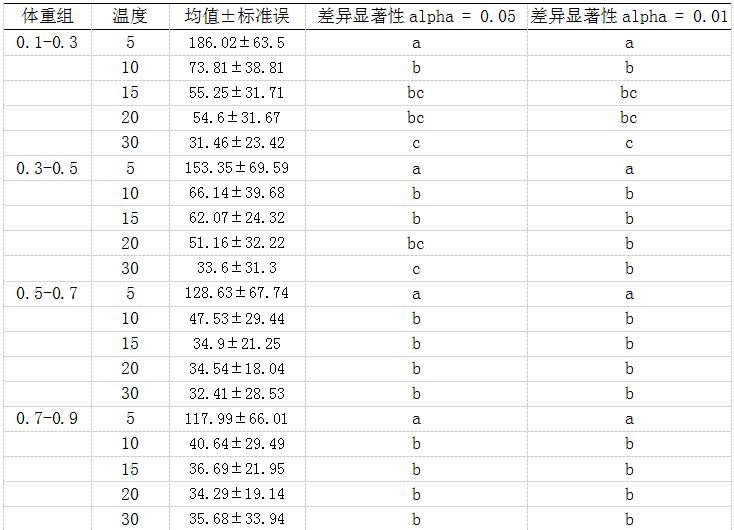
表2 同一体重组下,不同温度之间显著性分析结果
Table2. The significant results of different temperature at the same weight
从表2可以得出结论:
1.在alpha = 0.05水平上,对于体重组1,温度5和10、15、20、30有明显差异,温度10和30有明显差异;对于体重组2,温度5和10、15、20、30有明显差异,温度10、15、20和30有明显差异;对于体重组3和4,温度5和10、15、20、30有明显差异。
2.在alpha = 0.01水平上,对于体重组1,温度5和10、15、20、30有明显差异,温度10和30有明显差异;对于体重组2,温度5和10、15、20、30有明显差异;对于体重组3和4,温度5和10、15、20、30有明显差异。
结论:
由以上分析可以得出结论,蜗牛的初始体重和所处的温度都对取食量有一定的影响。在温度较低时,体重差别大的取食量差别也大,温度较高时则没有明显差别。在体重较低时,取食量受温度影响较为明显,在体重较高时,5℃和10℃及以上温度有明显差别,10℃、15℃、20℃、30℃之间则无明显差别。
注:本人非此专业学生,因此文中如有错误,恳请大家批评指正。
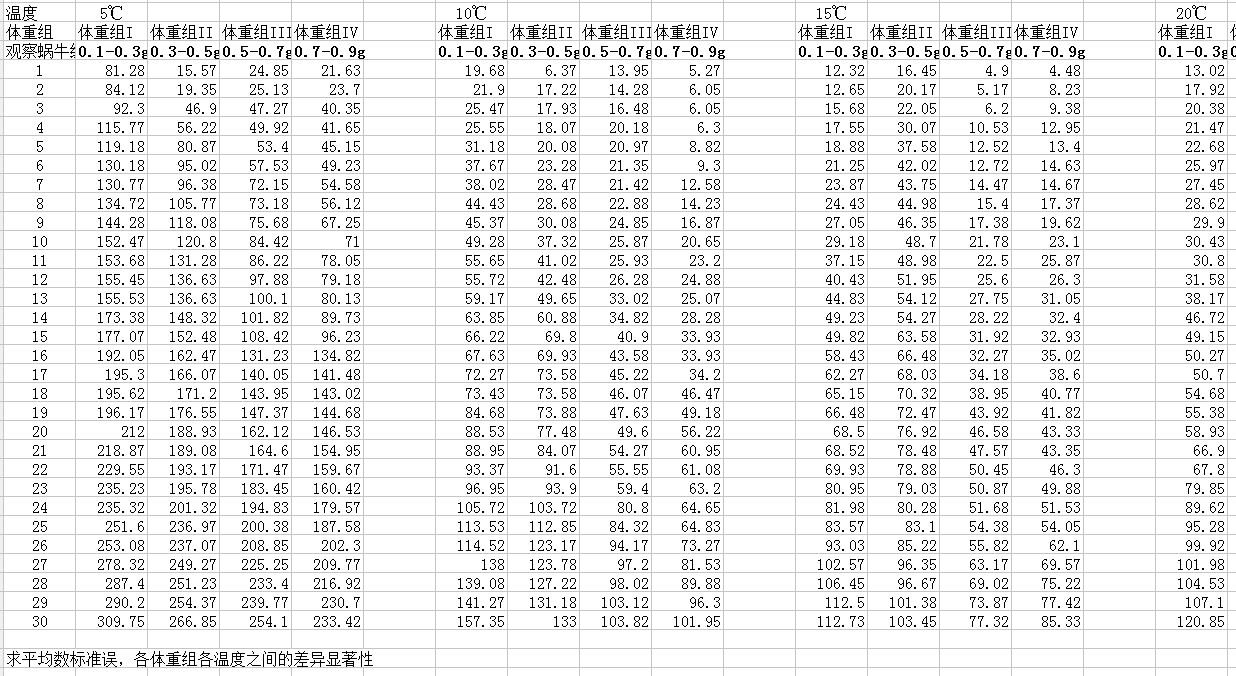
附Excel原始数据:
2019年6月21日update:原始数据已传百度网盘
链接: https://pan.baidu.com/s/1vvULATLX9Kj8j4Rf1-7kMw 提取码: 2wkp








 本文通过实例演示了如何使用SPSS进行多变量数据分析,包括数据输入、作图及多因素变量分析等步骤,并对不同温度和体重组条件下蜗牛取食量的影响进行了详细解读。
本文通过实例演示了如何使用SPSS进行多变量数据分析,包括数据输入、作图及多因素变量分析等步骤,并对不同温度和体重组条件下蜗牛取食量的影响进行了详细解读。
















 8278
8278

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








