方差分析中怎么看有无显著性影响_多变量方差分析实例分析

本文将分享多变量方差分析实例操作。

多变量方差分析用于研究控制变量对多个因变量的影响。多变量方差分析的基本原理与单变量方差分析的原理相似，用于分析控制因素取不同水平时因变量的均值是否存在显著性差异。但是，多变量方差分析在分析过程中还利用了各因变量协方差的相关信息。

实例分析

以下是某次对中小学校医采用三种方式进行培训后的知识水平测试和技能测试得分数据。下面将利用多变量方差分析的方法分析三种培训方式对校医的知识水平和技能两个因变量的影响，原始数据如图1所示。

注：在主页中回复20190920即可获取案例数据哦

图1 原始数据

01 数据录入

在SPSS的变量视图中建立变量“培训组”“知识水平得分”和“技能测试得分”，如图2所示。

图2 数据文件变量视图

在SPSS数据视图中，将相关数据输入到各个变量中，输入完毕后如图3所示。

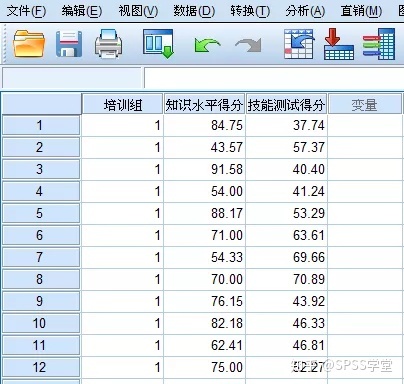
图3 数据文件数据视图

02 操作步骤

①在菜单栏中依次点击“分析”、“一般线性模型”、“多变量”命令，打开“多变量”对话框，如图4所示。

图4 多变量对话框

②将“知识水平得分”和“技能测试得分”选入因变量，将“培训组”选入“固定因子”列表，如图5所示。

图5 变量选择

③点击“模型”，选择“全因子”，其他默认，点击“继续” ，如图6所示。

图6多变量模型

④点击“两两比较”，将“培训组”选入“两两比较检验”列表框，选中“LSD”检验方法，点击“继续”，如图7所示。

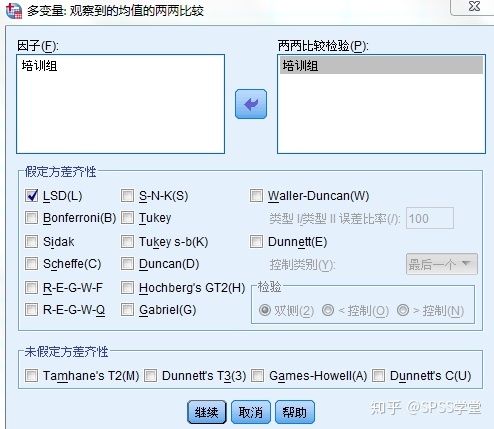
图7 两两比较

⑤点击“选项”，选中“描述统计”，点击 “继续”，如图8所示。

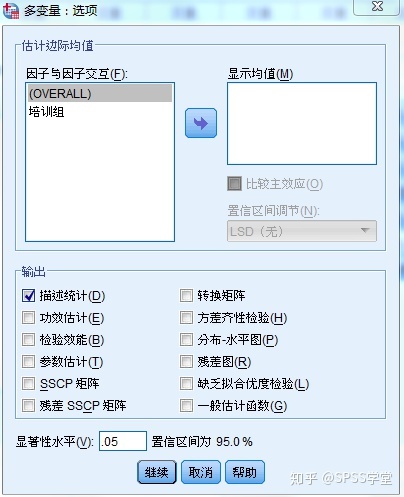
图8 选项

⑥点击“确定”，输出分析结果。

03 结果及分析

图9是本数据文件的一些描述性统计量。从该表可以得到，两个因变量“知识水平得分”和“技能测试得分”中各个小组的平均得分、标准偏差和个案数目。如第一组的“知识水平得分”平均分为71.1294，“技能测试得分”平均分为63.1404。

图9 描述性统计量表

从图10可以看出，各个检验的概率值都小于0.05，因此不同培训方法的影响是非常显著的。另外，比较“培训组”中的Pillai跟踪值和Hotelling的跟踪值，两者的分值分别是0.160和0.188，差距较小，说明各组对模型的影响较小。

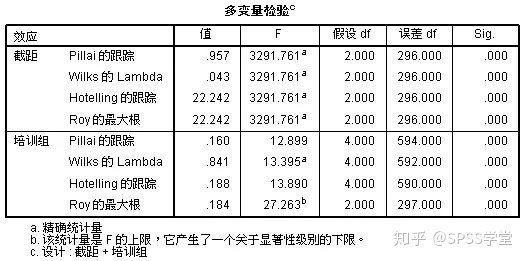
图10 多变量检验结果表

从图11可以看出，在0.05的显著性水平下，三种培训方法对“技能测试得分”的影响非常显著，而对“知识水平得分”的影响却不显著，对应的P值是0.227，大于显著性水平0.05。

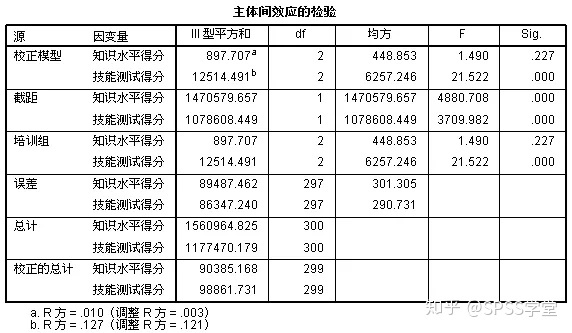
图11 多变量方差分析的结果

图12给出了多个比较的结果，*表示该组均值差是显著的，从该表可以看出，对技能的培训上，三种培训方法有显著的差别和影响能力。但三种培训方法对知识水平的影响既不显著也无明显的差别。

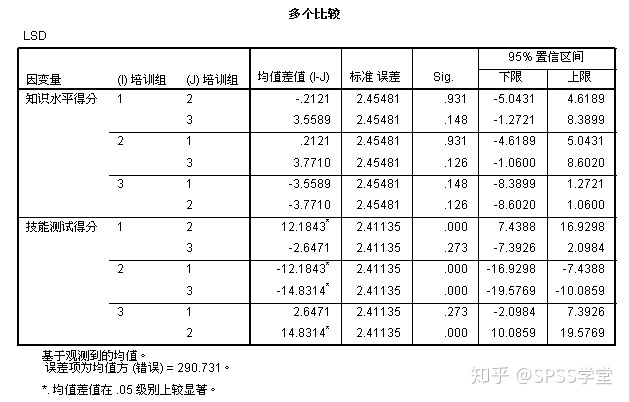
图12 多个比较结果表

以上是多变量方差分析实例分享，请大家多多练习哦！