关于λ-optimal的初始化解算法在(元)启发式中的应用

最新推荐文章于 2025-11-30 20:35:27 发布
最新推荐文章于 2025-11-30 20:35:27 发布
阅读量505 收藏 2
点赞数 2
CC 4.0 BY-SA版权
分类专栏： 组合优化 文章标签： 算法 人工智能 组合优化 元启发
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/wlfyok/article/details/127969835
本文介绍了λ-optimal算法在解决旅行推销员问题(TSP)时，如何作为有效的初始化解方法。通过对连续城市序列的操作，生成可能的TSP路径并不断优化，以提供后续启发式算法的初始解。文中还讨论了算法优化策略，包括避免重复序列和采用禁忌搜索思想来扩大解空间和提高效率。

关于λ-optimal算法在启发式中初始化解的应用


这里讨论组合优化中初始解的生成问题。组合优化问题，很多情况下，解的生成是随机的或者是采用某种直观上满足题意的初始化方法，要知道初始解对于找到局部最优乃至是最好的解是极其重要的，就好比条条大路通罗马，或者你直接就出生在罗马。接下来要说明的算法是在进行各种不同的启发式算法求解之前，对初始解进行优化的算法且比较通用。
在实际问题中，目前笔者暂时遇到的可以使用的地方一个是用于解的生成，还有一个地方就是在启发式算法迭代求解的过程中，在解的再生成中应用这种λ-optimal算法的思想。
描述问题或者算法要有头有尾，先说明问题，之后算法的描述建立在此之上，也就更加通俗易懂。

TSP问题介绍

旅行推销员问题可以这样表述:“要求推销员在给定的n个城市中访问一次且仅访问一次，从任意一个城市出发，返回出发地。他应该选择什么样的路线或旅行，以使总旅行距离最小化?”除了距离，还可以考虑时间、成本等其他概念。

在数学中，可以描述为：
在一个无向完全图中，把城市看作坐标点，每个城市之间都有路，且一般路径长度用欧氏距离描述

给定一个"成本矩阵" D = (D i j)，dij（i，j是下标）为i城市和j城市之间的距离成本，且dij=dji

P = (i1, i 2 , i2 ,… , in) 是城市的集合

而总的花销为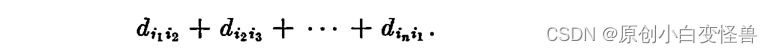在这里插入图片描述
目标函数是Q，公式为

了解本专栏 订阅专栏 解锁全文 超级会员免费看
人类决策行为的“有界最优性“：找到正确的算法在犯错误和思考太多之间找到完美的平衡
AI天才研究院
09-03 1103
在现代社会中，我们每天都面临着无数的决策。从选择早餐吃什么，到制定长期职业规划，决策无处不在。传统的经济学理论假设人类是完全理性的，能够在所有可能的选项中做出最优决策。然而，现实世界中的决策过程远比理论模型复杂。人类的认知能力是有限的，我们无法像计算机那样快速处理海量信息。这就引出了一个关键问题：在有限的时间和认知资源下，人类如何做出"足够好"的决策？这个问题导致了"有界最优性"（Bounded Optimality）概念的提出。
运筹优化（十四）--离散优化的启发式算法
热门推荐
工作笔记
01-19 3万+
启发式算法（heuristic algorithm)是相对于最优化算法提出的。一个问题的最优算法求得该问题每个实例的最优解。也就是说，在允许运行时长足够长的 情况下，确保得到一个最优方案。但是大量重要的ILP和INLP问题，并不存在多项式时间的解法，因此，启发式算法可以这样定义：一个基于直观或经验构造的算法，在可接受的花费（指计算时间和空间）下给出待解决组合优化问题每一个实例的一个可行解，该可行解...
数学建模启发式算法篇（一）---遗传算法
大学成长道路上的探索经历与点滴思考，与君共勉，共筑成长。
11-06 1751
1.引言 2.生物学基础 2.1适应度 2.2染色体，基因 3.算法介绍 3.1算法流程 3.2编码和解码 3.3轮盘赌选择 3.4交叉和变异 3.5初始参数的设置 4.实际应用-matlab 4.1观察图像 4.2初始参数说明 4.3init初始化 4.4二进制转换为十进制 4.5选择,交叉过程 4.6情况说明 4.7代码
启发式算法之遗传算法--求解组合优化问题
qq_38757869的博客
08-24 6954
本文为原创文章，如有任何疑问请留言 遗传算法是一种全局、概率搜索算法，主要用于求解大规模旅行商问题、路径规划问题、任务调度等NP-hard问题。 遗传算法属于进化算法，首先将需要求解的自变量通过编码形成染色体，在遗传过程中通过交叉、变异等操作产生新个体，选择种群中较优的个体遗传到下一代，不断进化，直到达到遗传终止条件为止。 本文以一个小规模的两两组合优化问题为例对遗传算法的流程进行简要介绍。...
使用启发式算法生成初始解输入Gurobi 中求解
Richard_Yang2016的博客
08-16 5134
今天看论文 Double row layout problem. 最后提到一种方法，使用启发式算法生成解当做初始解给Gurobi求解。这样的结合求解可以提高求解效率。 主要用到Yalmip 中的 assign 命令 以及 usex0 例如： x = sdpvar(1,1); assign(x,pi); optimize([sin(x)^2 usex0 The
启发式算法和元启发式算法
weixin_43200997的博客
10-12 5195
启发式算法 启发式算法（Heuristic Algorithm)是相对于最优化算法提出的。一个问题的最优算法求得该问题每个实例的最优解。启发式算法可以这样定义：一个基于直观或经验构造的算法，在可接受的花费（指计算时间和空间）下给出待解决组合优化问题每一个实例的一个可行解，该可行解与最优解的偏离程度一般不能被预计。 元启发式算法 元启发式算法（Meta-heuristic Algorithm）是启发式算法的改进，它是随机算法与局部搜索算法相结合的产物。元启发式策略通常会对搜索过程提出一些要求，然后按照这些要求
《Nature-Inspired Metaheuristic Algorithms》——蝙蝠算法 Bat Algorithm
qq_43336475的博客
02-27 1948
蝙蝠算法 蝙蝠的生物习性 蝙蝠的回声定位：蝙蝠通过发射非常响亮的声音脉冲并倾听周围物体发出的回声，以此来确定猎物的大小和自己与猎物之间的距离，来决定自己说加速/减速并向着猎物/远离猎物飞行。蝙蝠发出的脉冲具有回声频率和回声响度，回声频率与相对距离决定蝙蝠的速度，而速度与当前位置决定了蝙蝠下一刻的位置。回声频率会随着接近猎物而逐渐增大（因为需要更快确定猎物的位置），回声响度会随着接近猎物而逐渐减小（为了防止吓到猎物）。 事实上，蝙蝠的回声定位是一种非常复杂的机制，这里并没有完全按照其捕猎机制来模拟算法，而是
IJCAI-2020《Semi-supervised Clustering via Pairwise Constrained Optimal Graph》
Christo的博客
06-23 951
论文提出了一种基于图的半监督聚类方法，称为Pairwise Constrained Optimal Graph (PCOG)，旨在通过引入成对约束（必须链接 Must-Link 和不能链接 Cannot-Link）来指导聚类过程，解决传统图聚类方法在处理不能链接约束和多类聚类时的局限性。其核心思想包括：该方法解决了传统半监督聚类中不能链接约束难以处理和多类聚类灵活性不足的问题，显著提升了聚类性能。论文的目标函数旨在优化图的亲和矩阵SSS，使其满足成对约束并具有ccc个连通分量。初始目标函数形式为：min⁡S
基于路径重连的双目标迭代局部搜索启发式算法求解p-中位数问题
# 基于路径重连的双目标迭代局部搜索启发式算法求解 p - 中位数问题 ## 1 引言 在设施选址领域，单目标 p - 中位数问题（SO - p - MP）是一个经典问题。给定 n 个客户和 m 个潜在设施，该问题旨在找到一个包含 p 个...
启发式算法求解混合整数线性优化问题—— 生产计划安排和资源分配
yuuyuhaksho的博客
02-17 9122
问题描述和范围限定： 生产计划安排分为两种：静态和动态计划。 静态计划生成的时间距离实际生产时间较长，以假设所有预设条件都满足为前提，在给定优化目标下（比如最小延迟，最低库存金额，etc.）寻找最优计划。静态计划一般采用优化算法实现。 动态计划基于静态计划，是在实际排产出现异常时（比如原材料供应不足，设备突然故障造成停线，上游产品突发质量问题，产线工人罢工，etc.） 这篇文章主要关注生成静态计划...
模拟退火(SA)算法实例介绍（JAVA）
诸葛小猿
10-09 8685
模拟退火算法来源于固体退火原理，是一种基于概率的算法，将固体加温至充分高，再让其徐徐冷却，加温时，固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小。 模拟退火算法(Simulated Annealing，SA)最早的思想是由N. Metropolis 等人于1953年提出。1983 年,S. Kirkpatrick 等成功地将退火思想引入到组合优化领域。它是基于Monte-Carlo迭代求解策略的一种随机寻优算法，其出发点是基于物理
元启发式算法（智能算法）的思考
sinat_41348401的博客
07-02 3023
启发式算法一般是指“基于规则”的方法，能够直接给出一个解。 我们平时说的【智能算法】有的人也叫它启发式算法，其实不太对；或者说为了与前一种区分，通常叫做“元”启发式算法，meta-heuristics。这种通常是改进型算法，也就是通过种群或者邻域不断迭代予以改进。像邻域搜索，蚁群，蜂群等等都属于这一类。......
算法--位运算
最新发布
budingxiaomoli的博客
11-30 738
本文总结了常见的位运算原理及其应用。基础位运算包括左移、右移、按位取反、与或非等操作。重点介绍了位图思想在哈希表优化中的应用，以及提取/删除最右侧1的方法。通过5道LeetCode题目展示了位运算的实际应用：判断字符唯一性（位图优化）、寻找缺失数字（异或运算）、两数之和（无进位相加）、只出现一次数字（位统计）和消失的两个数（分类异或）。这些题目展示了位运算在节省空间、提高效率方面的优势，为解决算法问题提供了新的思路。
湘大头歌程-Ride to Office练习笔记
myw071205的博客
11-29 764
Charley骑车从起点到终点（4500米）需要有人陪伴骑行，遇到更快者会加速跟上。输入给出同行者的速度v和出发时间t，要求计算Charley到达终点的最短时间（小数向上取整）。关键思路是Charley最终会与最快到达终点的人同时到达。解题时忽略提前出发者，对每个同行者计算其到达时间t + ceil(4.5/v*3600)，取最小值作为答案。代码使用limits.h初始化最小值和math.h的ceil函数处理取整。后文详细介绍了limits.h的常量定义和math.h的四种取整函数的功能与区别
dfs|mask^翻转
一个人知道自己为什么而活，他就能够接收任何一种生活
11-30 118
注意到：灯泡状态周期是6。
进阶数学算法-取石子游戏(ZJOI2009)
Ayanami_Rei的博客
11-29 806
ZJOI 2009 取石子游戏
基于A*算法的雷雨绕飞路径MATLAB实现
2501_92729044的博客
11-30 168
本文提出了一种基于A算法的雷雨绕飞路径规划方法。该方法首先生成模拟雷雨天气图并进行二值化处理，识别危险区域；然后检测计划航路中需要绕飞的航段，通过A算法为每个航段生成左右绕飞候选路径；接着进行视距优化和平行路径拓展以提高安全性；最后整合各航段最优路径构建完整绕飞航路。实验结果表明，该方法能有效避开危险区域，生成安全且长度优化的绕飞路径。关键创新点包括：1) 结合雷达天气数据的精细化处理；2) 多候选路径生成与优化机制；3) 完整航路构建策略。可视化界面直观展示了各阶段路径规划效果。
【剑斩OFFER】算法的暴力美学——只出现一次的数字 ||
就业知识博客
11-24 671
力扣137题：只出现一次的数字 ||
【民族服饰识别系统】Python+TensorFlow+Vue3+Django+人工智能+深度学习+卷积网络+resnet50算法
子午的博客
11-30 720
民族服饰识别，民族服饰智能识别与分析系统基于TensorFlow框架，采用卷积神经网络（CNN）算法构建而成。系统在收集了回族、汉族、满族、苗族四类典型民族服饰图像数据集的基础上，通过多轮迭代训练，最终生成高精度识别模型，并配合Web可视化平台实现便捷交互。前端后端：Django算法：TensorFlow、卷积神经网络算法具体功能系统分为管理员和用户两个角色，登录后根据角色显示其可访问的页面模块。登录系统后可发布、查看、编辑文章，创建文章功能中集成了markdown编辑器，可对文章进行编辑。
智能路由算法
04-24
<think>好的，我现在需要帮助用户了解智能路由算法的实现原理和优化方案。根据用户的问题，他们可能对智能路由算法的基础概念、具体实现方法以及如何优化这些算法感兴趣。首先，我需要回顾已有的知识，特别是之前提到的蚁群算法在路由优化中的应用，因为用户之前的引用提到了这个。 首先，智能路由算法的核心目标应该是优化数据包的传输路径，提高网络效率。常见的智能算法包括蚁群算法、遗传算法、粒子群优化等。用户提到的蚁群算法，我需要详细解释其原理，比如信息素机制、路径选择策略，以及如何应用到路由中。 然后，关于实现原理，可能需要分步骤说明，比如初始化信息素、路径选择概率的计算、信息素更新等。这部分需要结合具体的例子，比如在Matlab中的实现步骤，但用户可能需要更通用的解释，而不仅仅是代码。 接下来是优化方案。用户可能想知道如何改进基础算法，比如动态调整参数、多目标优化、混合算法等。需要列举几种优化方法，并简要说明每种方法的优势，比如动态调整α和β参数来平衡探索与利用。 另外，用户可能对实际应用中的挑战感兴趣，比如收敛速度、局部最优问题等。需要提到这些挑战，并给出相应的解决方案，比如结合模拟退火来避免局部最优。 还需要考虑用户可能的后续问题，比如如何评估智能路由算法的性能，或者具体在某个网络环境中的应用案例。因此，在回答中需要涵盖这些方面，或者至少为后续问题埋下伏笔。 现在需要检查是否遵循了系统级指令，比如使用正确的中文，数学公式的格式是否正确。例如，在信息素更新公式中，使用$$...$$格式，变量如τ用$包裹。确保所有行内数学表达式正确，比如概率公式中的$P_{ij}^k(t)$。 另外，要生成相关问题，这些问题应该围绕用户可能感兴趣的扩展内容，比如与其他算法的比较、参数调整方法、实际应用场景等。确保问题具有连贯性和逻辑性，帮助用户深入探索主题。 最后，确认引用的正确使用，用户提供的引用是关于蚁群算法在多路径路由中的应用，需要在适当的地方加入引用标识，比如在讨论蚁群算法时引用[^1]。同时，保持回答结构清晰，分点说明，便于用户理解。</think>### 智能路由算法实现原理与优化方案 #### 一、智能路由算法实现原理 1. **核心思想** 智能路由算法通过模拟自然现象（如生物群体行为）或优化理论，动态选择最佳数据传输路径。以蚁群算法为例，其核心原理包括： - **信息素机制**：蚂蚁在路径上释放信息素$τ_{ij}(t)$，浓度越高表示路径越优[^1] - **概率选择公式**： $$P_{ij}^k(t) = \frac{[τ_{ij}(t)]^α \cdot [η_{ij}]^β}{\sum_{l∈N_k}[τ_{il}(t)]^α \cdot [η_{il}]^β}$$ 其中$η_{ij}=1/d_{ij}$为启发因子，$α,β$控制信息素与距离的权重 - **信息素更新**： $$τ_{ij}(t+1) = (1-ρ)τ_{ij}(t) + \sum_{k=1}^m Δτ_{ij}^k$$ $ρ∈(0,1)$为挥发系数，$Δτ_{ij}^k$为蚂蚁$k$在路径$(i,j)$上释放的信息素量 2. **实现步骤** 以多路径路由优化为例： ```matlab % 蚁群算法伪代码框架 initialize pheromone matrix τ; while not meet termination condition for each ant k construct path based on P_{ij}^k(t); calculate path quality; update pheromone matrix; apply evaporation; end select optimal paths; ``` #### 二、优化方案 1. **参数动态调整** - 自适应调整$α,β$：初期增大$β$加速收敛，后期增强$α$避免局部最优 - 挥发系数$ρ$随迭代次数变化： $$ρ(t) = ρ_{min} + (ρ_{max}-ρ_{min}) \cdot e^{-λt}$$ 2. **混合优化策略** - 结合模拟退火算法：以概率$p=exp(-ΔE/T)$接受次优解，增强全局搜索能力 - 集成Q-learning：建立状态-动作价值函数$Q(s,a)$，实现动态环境适应 3. **多目标优化** $$min\{f_1(延迟),f_2(丢包率),f_3(能耗)\}$$ 采用Pareto前沿分析，使用NSGA-II算法处理多目标约束 4. **分层路由架构** - 控制平面：集中式路径计算（SDN控制器） - 数据平面：分布式智能决策（边缘节点） #### 三、典型挑战与对策 | 挑战 | 解决方案 | |------|----------| | 收敛速度慢 | 引入精英蚂蚁策略，保留最优路径信息素 | | 局部最优陷阱 | 结合遗传算法的变异操作 | | 动态网络环境 | 设计滑动时间窗口机制，实时更新拓扑信息 |
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

原创小白变怪兽

帮助原创小白成为怪兽吧！

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值