Codeforces Round 1007 (Div. 2)（部分题解）

A. The Play Never Ends

思路：自己推一两种情况，就会发现规律。

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'

void solve()
{
    int n;
    cin >> n;
    if (n%3 == 1){
        cout << "YES" << endl;
    }
    else cout << "NO" << endl;
}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    
    int t = 1;
    cin >> t;
    while (t--)
    {
        solve();
    }
    
    return 0;
}

B. Perfecto

思路：首先判断n个数的总和是否是平方数，是的话肯定输出-1，然后我们是输出先输出2   1，再输出3  4  5   6往后，并统计总和，遇到是平方数的就让该位与下一位交换一下。

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
int check(int x){
    int cnt = sqrt(x);
    if (cnt*cnt == x) return 0;
    return 1;
}
void solve()
{
    int n, m, k;
    cin >> n;
    int res = (n+1)*n/2;
    int mm = sqrt(res);
    if (!check(res)){
        cout << -1 << endl;
        return ;
    }
    int sum = 3;
    if (n >= 2){
        cout << 2 << " " << 1 << " ";
        for (int i = 3; i<=n; i++){
            if (!check(sum+i)){
                cout << i+1 << " " << i << " ";
                sum += i*2+1;
                i++;
            }
            else {
                cout << i << " ";
                sum += i;
            }
        }
        cout << endl;
    }

}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    
    int t = 1;
    cin >> t;
    while (t--)
    {
        solve();
    }
    
    return 0;
}

C. Trapmigiano Reggiano

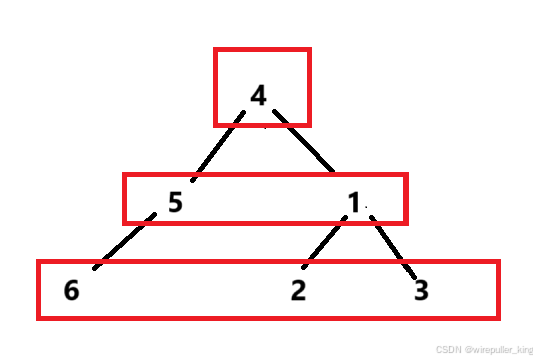
思路：感觉官方题解是一个神奇结论：处理了最大深度 n−1 的所有顶点后，鼠标当前的深度不能超过 n−1。对下一个最大深度 n−2重复这一过程后，鼠的深度将不可避免地变为 n−2或更小。这样继续下去，我们就会按照深度从大到小的顺序处理顶点，直到我们到达根节点，从而达到我们想要的结果。

这样它就能一直往en点靠近。

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define vi vector<int>
#define vvi vector<vi>
#define pb push_back
#define endl '\n'
void solve()
{
    int n, st, en;
    cin >> n >> st >> en;
    vector<vector<int>> adj(n+1);
    for (int i=1; i<n; i++){
        int u, v;
        cin >> u >> v;
        adj[u].pb(v);
        adj[v].pb(u);
    }
    vector<vector<int>> dis(n+1);
    vector<int> dep(n+1, 0);
    auto dfs = [&](auto && dfs, int u, int fa)->void
    {
        dep[u] = dep[fa]+1;
        dis[dep[u]].pb(u);
        for (int v : adj[u]){
            if (v == fa) continue;
            dfs(dfs, v, u);
        }
    };
    dep[en] = 1;
    dfs(dfs, en, 0);
    for (int i=n; i>=1; i--){
        for (int u : dis[i]){
            cout << u << " ";
        }
    }
    cout << endl;
}
signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    
    int t = 1;
    cin >> t;
    while (t--)
    {
        solve();
    }
    
    return 0;
}

D1. Infinite Sequence (Easy Version)

思路：难点主要在分类讨论和递归。

当p<=n时，直接返回a[i];

当p/2<=n时，返回异或前缀s[p/2];

接下来讨论递归的分类，要求的是前q/2的异或：

qnow = q/2 > n,

当n是奇数时：

（1）qnow  是偶数时（8），中间的n+1到qnow的数可以两两异或掉，所以只用s[n]异或a[qnow]的值，a[qnow]的值通过递归寻找。

 

（2）qnow  是偶数时（9），a[n+1]到a[qnow]两两异或掉了，所以返回s[n];

当n是偶数时：

（1）qnow  是偶数时（8）时，a[n+2]到a[qnow-1]两两异或掉，所以只用s[n]异或a[qnow]异或a[n+1]的值，a[qnow],a[n+1]的值通过递归寻找。

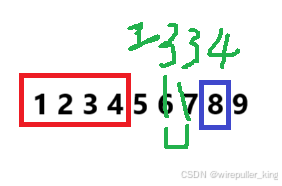
（2）qnow  是偶数时（9）时，a[n+2]到a[qnow]两两异或掉了，所以返回s[n]异或a[n+1],a[n+1]的值通过递归寻找;

AC代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
void sovle(){
	int n, l, r;
	cin >> n >> l >> r;
	vector<int> a(n+1), s(n+1);
	for (int i = 1; i<=n; i++){
		cin >> a[i];
		s[i]=s[i-1]^a[i];
	}
	auto dfs = [&](auto &&dfs, int p)->int
	{
		if (p <= n) return s[p];
		if (p/2 <= n) return dfs(dfs, p/2);
		p/=2;
		if (n&1){
			if (p&1) return s[n];
			else return s[n]^(dfs(dfs, p));;
		}
		else{
			if (p&1) return s[n]^dfs(dfs,n+1);
			else return dfs(dfs, p)^s[n]^dfs(dfs, n+1);
		}
		return 0;
	};
	if (r <= n){
		cout << a[r] << endl;
	}
	else cout << dfs(dfs, r) << endl;
}
signed main(){
	int t;
	cin >> t;
	while (t--){
		sovle();
	}
	return 0;
}