什么是仿射变换?
仿射变换就是图像的线性变换加上平移,用一幅图表示,就是
由 image1 到 image2 的转换经过了三个操作
- 旋转 (线性变换)
- 缩放操作(线性变换)
- 平移 (向量加)
如果没有了第3个平移的操作,那它就是线性变换。前两个笔记已经整理了图像的旋转、缩放和平移的各个方法,接下来会介绍仿射变换的矩阵表示和使用方法。
放射变化的矩阵形式
图像的变换要对图像的每一个像素点进行操作,假设其中的一个像素点的坐标是(x,y),我们用矩阵形式表示: 
我们通常使用 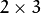 矩阵来表示仿射变换。
矩阵来表示仿射变换。
矩阵
A、B 就是变换矩阵
经过仿射变换后的点的矩阵坐标是T,我们已经知道放射变换就是线性变换加上平移,用矩阵表示的话就是 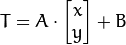
也可以写成 ![T = M \cdot [x, y, 1]^{T}](http://www.opencv.org.cn/opencvdoc/2.3.2/html/_images/math/f44f98e19b4ee0613633b70414a47259846b2d27.png)
计算可得 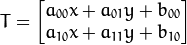
使用代码
来看一下之前说过的图像平移的代码
import cv2
import numpy as np
img = cv2.imread('Rachel.jpg', 0)
rows, cols = img.shape
M = np.float32([[1, 0, 200], [0, 1, 100]])
dst = cv2.warpAffine(img, M, (cols, rows))
cv2.imshow('img', dst)
k = cv2.waitKey(0)
if k == ord('s'):
cv2.imwrite('Rachel3.jpg', dst)
cv2.destroyAllWindows() M = np.float32([[1, 0, 200], [0, 1, 100]])将这个二维矩阵的值带入T,得到经过仿射变换后的点的坐标是(x+200,y+100),即将整个图像平移(200,100)
再看图像旋转的代码
import cv2
img = cv2.imread('Rachel.jpg', 0)
rows, cols = img.shape
M = cv2.getRotationMatrix2D((cols / 2, rows / 2), 90, 1)
dst = cv2.warpAffine(img, M, (cols, rows)) # 仿射变换,以后再说
cv2.imshow('Rachel', dst)
cv2.waitKey(0)
cv2.destroyAllWindows() 大部分同上类似,只是其中的 M 矩阵不同
M = cv2.getRotationMatrix2D((cols / 2, rows / 2), 90, 1) # 第一个参数是中心点的坐标 cv2.getRotationMatrix2D这个函数就是生成图像旋转的所需要的矩阵
那么如何通过仿射变换任意变换图形呢?
我们需要源图像和目标图像上分别一一映射的三个点来定义仿射变换
示例代码:
img = cv2.imread('Rachel.jpg')
rows, cols, ch = img.shape
pts1 = np.float32([[0, 0], [cols - 1, 0], [0, rows - 1]])
pts2 = np.float32([[cols * 0.2, rows * 0.1], [cols * 0.9, rows * 0.2], [cols * 0.1, rows * 0.9]])
M = cv2.getAffineTransform(pts1, pts2)
dst = cv2.warpAffine(img, M, (cols, rows))
cv2.imshow('image', dst)
k = cv2.waitKey(0)
if k == ord('s'):
cv2.imwrite('Rachel1.jpg', dst)
cv2.destroyAllWindows()结果:







 本文介绍了仿射变换的概念及其矩阵表示方法,并通过实例演示了如何利用Python进行图像的平移、旋转及任意变换。
本文介绍了仿射变换的概念及其矩阵表示方法,并通过实例演示了如何利用Python进行图像的平移、旋转及任意变换。



















 1647
1647










