动态规划-最优二叉搜索树-公式推导

 

 

 

#include <iostream>
#include<bits/stdc++.h>
using namespace std;

const int MaxVal = 9999;

const int n = 5;

//搜索到根节点和虚拟键的概率
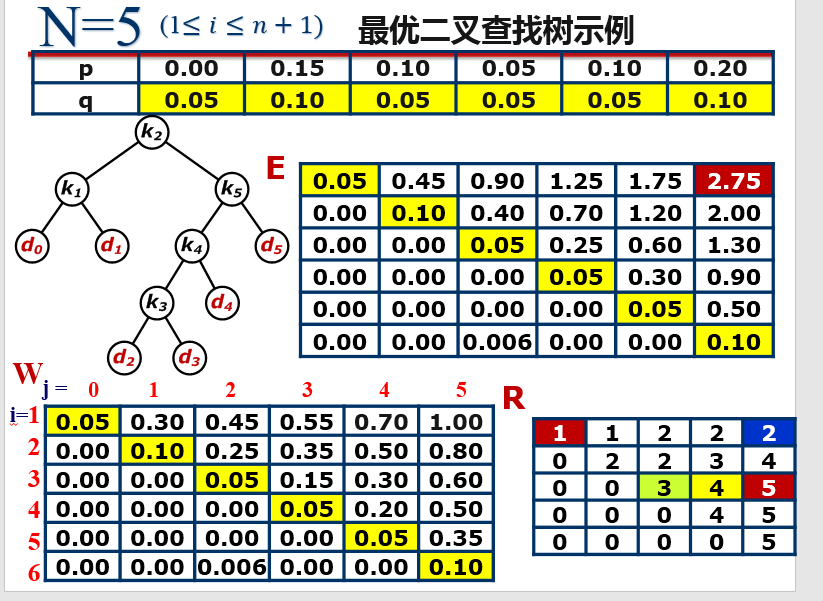
double p[n + 1] = {0, 0.15, 0.1 , 0.05 , 0.1,0.2};
double q[n + 1] = {0.05, 0.1 ,0.05,0.05,0.05, 0.1};

int    root[n + 1][n + 1];//记录根节点
double w[n + 2][n + 2];//子树概率总和
double e[n + 2][n + 2];//子树期望代价

void optimalBST(double *p,double *q,int n)
{
    //初始化只包括虚拟键的子树
    for (int i = 1;i <= n + 1;++i)
    {
        w[i][i - 1] = q[i - 1];
        e[i][i - 1] = q[i - 1];
    }

    //由下到上，由左到右逐步计算
    for (int len = 1 ; len <= n; len++ )
    {
        for (int j = n - len + 1 ; j <= n ; j++)
        {
            int i = n - len + 1;// i 从5到1

            e[i][j] = MaxVal;
            w[i][j] = w[i][j - 1] + p[j] + q[j];//公式推导、

            /*
            cout<<"w "<<i<<" "<<j - 1<<" "<<w[i][j - 1]<<endl;
            cout<<"p "<<j<<" "<<p[j]<<endl;

            cout<<"q "<<j<<" "<<q[j]<<endl;
            cout<<"w "<<i<<" "<<j<<" "<<w[i][j]<<endl;
            //cout<<"w"<<i<<j<<w[i][j]<<endl;
            //cout<<w[i][j]<<endl;
            getchar();
            */

            //求取最小代价的子树的根
            for (int k = i;k <= j;++k)
            {
                double temp = e[i][k - 1] + e[k + 1][j] + w[i][j];
                if (temp < e[i][j])
                {
                    /*
                    cout<<k<<endl;
                    cout<<i<<" "<<k-1<<"e "<<e[i][k - 1]<<endl;
                    cout<<k+1<<" "<<j<<"e "<<e[k + 1][j]<<endl;
                    cout<<i<<" "<<j<<"w "<<w[i][j]<<endl;
                    cout<<temp<<endl;

                    getchar();*/
                    e[i][j] = temp;
                    root[i][j] = k;
                }
            }
        }
    }
}

//输出最优二叉查找树所有子树的根


//打印最优二叉查找树的结构
//打印出[i,j]子树，它是根r的左子树和右子树

void printOptimalBST(int i,int j,int r)
{
    int rootChild = root[i][j];//子树根节点

    if (rootChild == root[1][n])
    {
        //输出整棵树的根
        cout << "k" << rootChild << "是根" << endl;
        printOptimalBST(i,rootChild - 1,rootChild);
        printOptimalBST(rootChild + 1,j,rootChild);
        return;
    }

    if (j < i - 1)
    {
        return;
    }
    else if (j == i - 1)//遇到虚拟键
    {
        if (j < r)
        {
            cout << "d" << j << "是" << "k" << r << "的左孩子" << endl;
        }
        else
            cout << "d" << j << "是" << "k" << r << "的右孩子" << endl;
        return;
    }
    else//遇到内部结点
    {
        if (rootChild < r)
        {
            cout << "k" << rootChild << "是" << "k" << r << "的左孩子" << endl;
        }
        else
            cout << "k" << rootChild << "是" << "k" << r << "的右孩子" << endl;
    }

    printOptimalBST(i,rootChild - 1,rootChild);
    printOptimalBST(rootChild + 1,j,rootChild);
}

int main()
{
    optimalBST(p,q,n);
    cout << "最优二叉树结构：" << endl;
    printOptimalBST(1,n,1);
}