【LeetCode】108. 将有序数组转换为二叉搜索树

题目描述

难度：【简单】
标签：【二叉树】

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 高度平衡 二叉搜索树。

高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

题目地址：https://leetcode-cn.com/problems/convert-sorted-array-to-binary-search-tree/

示例

示例 1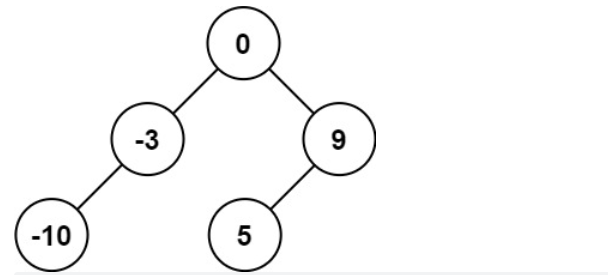

输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]

解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：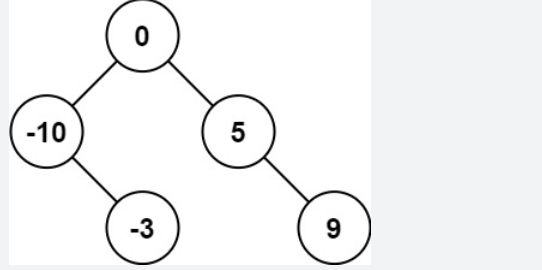

示例 2：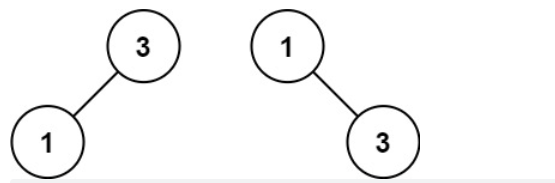

输入：nums = [1,3]
输出：[3,1]
解释：[1,3] 和 [3,1] 都是高度平衡二叉搜索树。

题目大意

给了一个已知整数数组，并且升序排列，转成一个高度平衡二叉搜索树。

解题

先看这个升序的数组，在二叉搜索树的三种遍历方式中，中序遍历是符合升序的。

那么可以把这个数组当做就是一个BST 中序遍历后的结果，问题是怎么创建出这个BST？而且是个高度平衡。

为了保持高度平衡，可以选择中间数字作为二叉搜索树的根节点，这样分给左右子树的数字个数相同或只相差 1，可以使得树保持平衡。

比如说输入的数组为[-10,-3,0,5,9]，元素偶数个，中间的元素是 0，把 0 当做根节点，如下BST 都可以输出这个中序遍历结果(参考官方图)。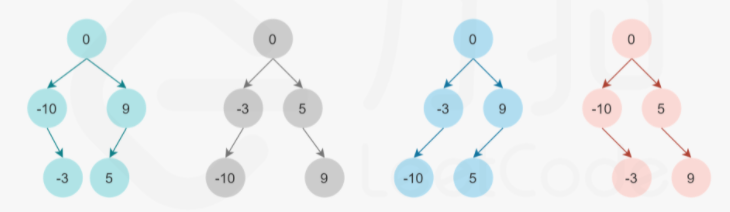

接下来就可以定义函数了，明确这个函数的作用，然后把剩下的事情交给框架，不要陷入递归的细节中。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        return createBST(nums, 0, nums.length-1);
    }
    public TreeNode createBST(int[] nums, int left, int right) {
        // 递归终止条件
        if (left > right) {
            return null;
        }
        // 选择其中数组中间位置 左边的数作为 根节点
        // 运算符/ 运算结果遵从向下取整，[1,2,3,4]偶数个，会取下标为1的元素
        int mid= (left + right) / 2;
        // 创建树的根节点
        TreeNode root = new TreeNode(nums[mid]);
        // 前序遍历框架
        root.left = createBST(nums, left, mid - 1);
        root.right = createBST(nums, mid + 1, right);
        return root;
    }
}

数组里有2个指针left 和 right，别忘记要定义出终止移动的条件left > right。

然后就是先创建出这个根节点，剩下的就是根节点左右子树的递归，所以从框架来看，这题仍使用前序遍历。