MATLAB应用实战系列NSGA-II多目标优化算法原理及应用实例（附MATLAB代码）

前言 

NSGA-Ⅱ是最流行的多目标遗传算法之一，它降低了非劣排序遗传算法的复杂性，具有运行速度快，解集的收敛性好的优点，成为其他多目标优化算法性能的基准。

NSGA-Ⅱ算法是 Srinivas 和 Deb 于 2000 年在 NSGA 的基础上提出的，它比 NSGA算法更加优越：它采用了快速非支配排序算法，计算复杂度比 NSGA 大大的降低；采用了拥挤度和拥挤度比较算子，代替了需要指定的共享半径 shareQ，并在快速排序后的同级比较中作为胜出标准，使准 Pareto 域中的个体能扩展到整个 Pareto 域，并均匀分布，保持了种群的多样性；引入了精英策略，扩大了采样空间，防止最佳个体的丢失，提高了算法的运算速度和鲁棒性。

以下是博主精心整理的两个matlab专栏，包含入门到精通及实战内容，需要的小伙伴可根据自己需求自行订阅。

MATLAB-30天带你从入门到精通

https://blog.youkuaiyun.com/wenyusuran/category_10614422.html

MATLAB深入理解高级教程（附源码）

https://blog.youkuaiyun.com/wenyusuran/category_2239265.html

需要详细源码的小伙伴可参见：

数学建模源码集锦-基于遗传算法的多目标优化算法应用实例

https://download.youkuaiyun.com/download/wenyusuran/15749792

NSGA-II与常规遗传算法的区别

选择过程分两个部分：
1. 把种群分成一组Pareto非支配集。一个非支配集里的个体不被当前或之后非支配集里的任何个体支配。方法就是每次选出所有不被任何其他个体支配的非支配个体，从种群里删除当一个非支配集，然后剩下的再不停重复这个过程，直到取完。
2. 按crowd distance排序。就是在各个维度左右相邻个体的距离之和。

NSGA-II关键算法

1.先对M个个体求pareto解。然后得到F1，F2……等这些pareto的集合。
2.把F1的所有个体全部放入N，若N没满，继续放F2，直到有Fk不能全部放入已经放入F1、F2、…、F(k-1)的N（空间）。此时对Fk进行求解。
3.对于Fk中的个体，求出Fk中的每个个体的拥挤距离Lk[i](crowding distance)，在fk中按照Lk[i]递减排序，放入N中，直到N满。

 

NSGA-II关键子程序算法

NSGA-II在常规遗传算法上的改进，关键步骤就3步。

 

1）快速非支配排序算子的设计

 

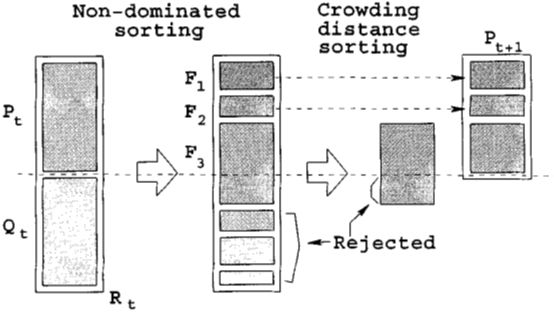
多目标优化问题的设计关键在于求取Pareto最优解集。NSGA-II算法中的快速非支配排序是根据个体的非劣解水平对种群分层，其作用是指引搜索向Pareto最优解集方向进行。它是一个循环的适应值分级过程：首先找出群体中非支配解集，记为第一非支配层F，将其所有个体赋予非支配序值irank=1(其中irank是个体i的非支配排序值)，并从整个种群中除去；然后继续找出余下群体中非支配解集，记为第二非支配排序层F2，个体被赋予非支配序值irank=2；照此进行下去，直到整个种群被分层，同一分层内的个体具有相同的非支配序值irank。

 

2）个体拥挤距离算子设计

 

为了能够在具有相同irank的个体内进行选择性排序，NSGA-II提出了个体拥挤距离的概念。个体i的拥挤距离是目标空间上与i相邻的2个个体i+1和i-1之间的距离，其计算步骤为：

a)对同层的个体初始化距离。令L[i]d=0（其中L[i]d表示任意个体i的拥挤距离）；

b)对同层的个体按第m个目标函数值升序排列；

c)使得排序边缘上的个体具有选择优势。给定一个大数M，令L[1]d=L[end]d=M；

d)对排序中间的个体，求拥挤距离：

（其中：L[i+1]m为第i+1个个体的第m目标函数值，和分别为集合中第m目标函数值的最大值和最小值）

e)对不同的目标函数，重复步骤a)~步骤d)操作，得到个体i的拥挤距离L[i]d，通过优先选择拥挤距离较大的个体，可使计算结果在目标空间比较均匀分布，以维持种群的多样性。

 

3）精英策略选择算子

 

精英策略即保留父代中的优良个体直接进入子代，以防止获得的Pareto最优解丢失。精英策略选择算子按3个指标对由父代Ci和子代Di合成的种群Ri进行优选，以组成新的父代种群Ci+1。首先淘汰父代中方案校验标志为不可行的方案；其次按照非支配序值irank从低到高排序，将整层种群依次放入Ci+1，直到放入某一层Fj时出现Ci+1大小超过种群规模限制N的情况；最后，依据Fj中的个体拥挤距离由大到小的顺序继续填充Ci+1直到种群数量达到N时终止。

下面这个图片能很好的说明NSGA-II的实现过程

---

最后附上用NSGA-II求解ZDT1函数的MATLAB代码，ZDT1函数如下：

 

 

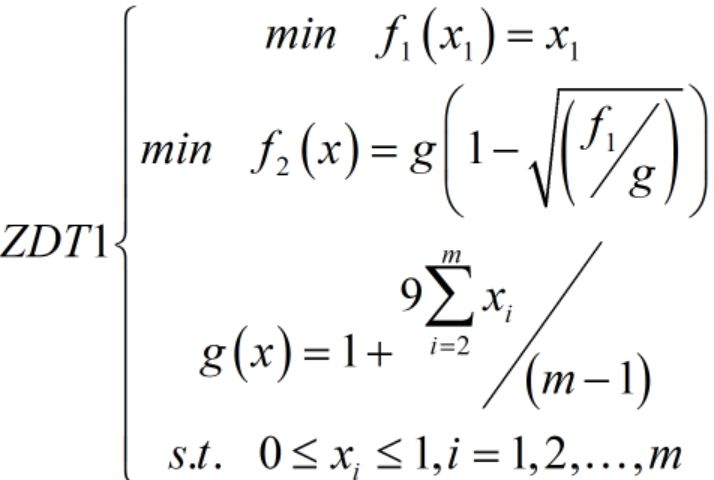
源代码解析

01  | 主函数Main NSGA2

 

主函数Main_NSGA2，运行主函数的时候，命令行窗口会出现Test problem index  :，这时需要输入1~14中的任意一个数字，意思就是选择14个测试函数中的任意一个函数。

%% https://ww2.mathworks.cn/matlabcentral/fileexchange/49806-matlab-code-for-constrained-nsga-ii-dr-s-baskar-s-tamilselvi-and-p-r-varshini
clear all
clc
global V M xl xu etac etam p pop_size pm

%% Description

% 1. This is the main program of NSGA II. It requires only one input, which is test problem
%    index, 'p'. NSGA II code is tested and verified for 14 test problems.
% 2. This code defines population size in 'pop_size', number of design
%    variables in 'V', number of runs in 'no_runs', maximum number of
%    generations in 'gen_max', current generation in 'gen_count' and number of objectives
%    in 'M'.
% 3. 'xl' and 'xu' are the lower and upper bounds of the design variables.
% 4. Final optimal Pareto soutions are in the variable 'pareto_rank1', with design
%    variables in the coumns (1:V), objectives in the columns (V+1 to V+M),
%    constraint violation in the column (V+M+1), Rank in (V+M+2), Distance in (V+M+3).
%% code starts
M=2;
p=input('Test problem index  :');
pop_size=200;           % Population size
no_runs=1;              % Number of runs
gen_max=500;            % MAx number of generations - stopping criteria
fname='test_case';      % Objective function and constraint evaluation

if p==13  % OSY
    pop_size=100;
    no_runs=10;
end
if (p==2 || p==5 || p==7), gen_max=1000; end

if p<=9     % Unconstrained test functions
    tV=[2;30;3;1;30;4;30;10;10];
    V=tV(p);
    txl=[-5*ones(1,V);zeros(1,V);-5*ones(1,V);-1000*ones(1,V);zeros(1,V);-1/sqrt(V)*ones(1,V);zeros(1,V); 0 -5*ones(1,V-1);zeros(1,V)];
    txu=[10*ones(1,V); ones(1,V);5*ones(1,V);1000*ones(1,V);ones(1,V);1/sqrt(V) *ones(1,V);ones(1,V);1 5*ones(1,V-1);ones(1,V)];
    xl=(txl(p,1:V));            % lower bound vector
    xu=(txu(p,1:V));            % upper bound vectorfor
    etac = 20;                  % distribution index for crossover
    etam = 20;                  % distribution index for mutation / mutation constant
else         % Constrained test functions
    p1=p-9;
    tV=[2;2;2;6;2];
    V=tV(p1);
    txl=[0 0 0 0 0 0;-20 -20 0 0 0 0;0 0 0 0 0 0;0 0 1 0 1 0;0.1 0 0 0 0 0];
    txu=[5 3 0 0 0 0;20 20 0 0 0 0;pi pi 0 0 0 0;10 10 5 6 5 10;1 5 0 0&n