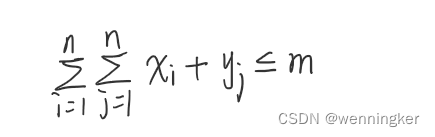
import math
def write_con(n,path,m):
f = open(path,"a",encoding = "utf-8")
for i in range(1,n):
f.write("x" + str(i) 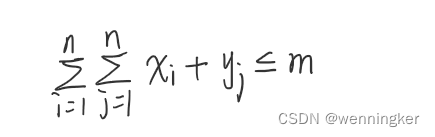
import math
def write_con(n,path,m):
f = open(path,"a",encoding = "utf-8")
for i in range(1,n):
f.write("x" + str(i) 
 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


