非线性控制（3）——时不变系统的稳定性分析

最新推荐文章于 2025-10-26 10:49:04 发布

原创最新推荐文章于 2025-10-26 10:49:04 发布 · 1.7k 阅读

34 ·

CC 4.0 BY-SA版权

文章标签：

#学习

非线性控制专栏收录该内容

3 篇文章

订阅专栏

本文介绍了Lyapunov方法在非线性控制理论中的应用，包括Lyapunov函数的概念、如何构造Lyapunov函数以证明系统稳定性，以及线性化的Lyapunov间接方法。着重讨论了如何利用Lyapunov方法估计吸引域，指出需要考虑轨线在定义域内的行为以确保稳定性结论的有效性。

#本系列文章为笔者自学非线性控制理论的学习记录，如有不正之处欢迎指正

#参考书籍《非线性控制》Hassan K. Khalil

1.Lyapunov方法

1.1定理描述

设 $D\in R^{n}$ 是包含原点的一个区域， $f(x)$ 为定义在D上的局部Lipschitz函数，且 $f(0)=0$ ，令 $V(x)$ 是定义在D上的连续可微函数，且满足

$V(0)=0,V(x)>0(x\in D,x\neq 0)\; \; \; \; \; \; \; \; \; \; (1)$

$\dot{V(x)}\leq 0(x\in D)\; \; \; \; \; \; \; \; \; \; (2)$

则原点是f(x)的稳定平衡点，如果进一步有：

$\dot{V}(x)< 0(x\in D,x\neq 0)\; \; \; \; \; \; \; \; (3)$

则原点是f(x)的渐进稳定平衡点。

如果 $D=R^{n}$ ，式(1)(3)对所有 $x\neq 0$ 均成立，且 $\left \| x \right \|\rightarrow \infty \Rightarrow V(x)\rightarrow \infty$

则原点是全局渐进稳定的。

1.2直观解释

如果一个连续可微函数V（x）满足上述的定义，则称V（x）为Lyapunov函数，对固定的 $c> 0$ ，集合 $\left \{ x,V(x)=c \right \}$ 称为一个Lyapunov面。下图显示了伴随c的增加Lyapunov面的变动情况。式(2)表明，当轨线穿过某个Lyapunov面时，总是向集合 $\Omega=\left \{ V(x)\leq c \right \}$ 内部走的，并且不再出来。当满足式(3)时，轨线从一个Lyapunov面走向其内部c值更小的Lyapunov面，随着c的减小，最终Lyapunov面将收缩于原点，表明随着时间增长，轨线也将趋于原点。

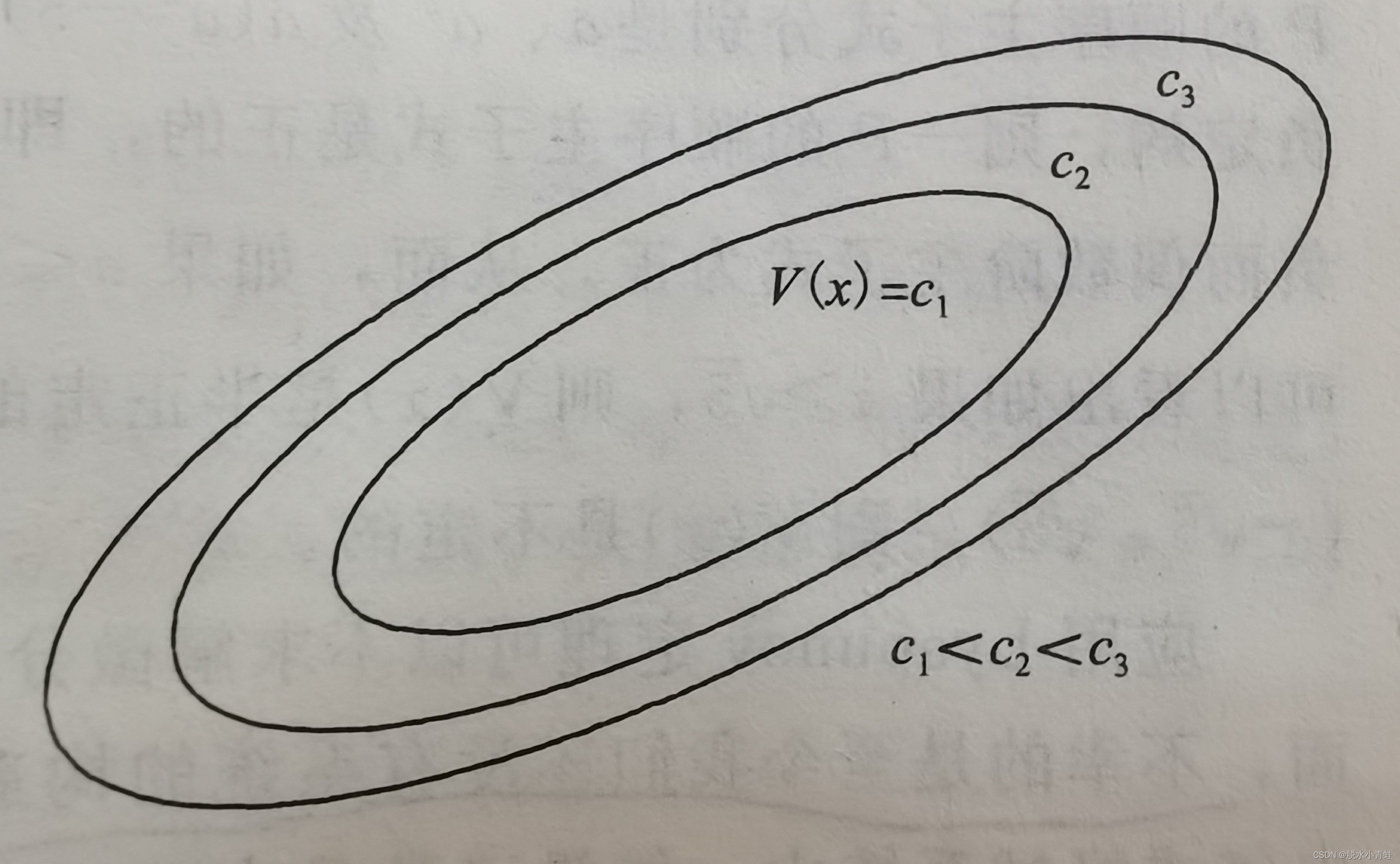
注：Lyapunov定理的条件仅仅是充分的，备选Lyapunov函数不能满足稳定或渐进稳定条件，并不能说明平衡点是不稳定或非渐进稳定的，而只是表明该备选函数不能确定平衡点稳定的性质。

1.3构造Lyapunov函数的一般方法

变量梯度法：先研究 $\dot{V}(x)$ 的表达式，再选取 $V(x)$ 的参数，使 $\dot{V}(x)$ 负定。方法介绍如下：

设 $V(x)$ 为x的标量函数，设 $g(x)=\triangledown V=(\frac{\partial V}{\partial x})^{T}$ ， $V(x)$ 沿着 $\dot{x}=f(x)$ 轨线的导数 $\dot{V}(x)$ 为：

$\dot{V}(x)=\frac{\partial V}{\partial x}\dot{x}=\frac{\partial V}{\partial x}f(x)=g^{T}(x)f(x)$

下面选取g(x)，它是正定函数 $V(x)$ 的梯度，同时又使 $\dot{V}(x)$ 负定。

g(x)为一标量函数的梯度当且仅当它的Jacobi矩阵是对称的，即 $\frac{\partial g_{i}}{\partial x_{j}}=\frac{\partial g_{j}}{\partial x_{i}},\forall i,j=1,2...n$

在此约束条件下，选择g(x)使 $g^{T}(x)f(x)$ 是负定的，最终V(x)由下式积分求得：

$V(x)=\int_{0}^{x}g^{T}(y)dy$

2.线性化（Lyapunov间接方法）

当原点是非线性系统的平衡点时，其稳定性可以通过研究线性系统在该平衡点的稳定性得出。

定理1：设x=0是非线性系统 $\dot{x}=f(x)$ 的一个平衡点，f(x)在原点的一个邻域内连续可微，设

$A=\frac{\partial f}{\partial x}|_{x=0}$

记其特征值为 $\lambda _{1},\lambda _{2}...\lambda _{n}$ ，那么：

(1)当且仅当所有特征值满足 $Re \left [ \lambda _{i} \right ] <0$ ，原点是指数稳定的；(此时称A为Hurwitz矩阵)

(2)当且仅当所有特征值满足 $Re \left [ \lambda _{i} \right ] >0$ ，原点是不稳定的。

该定理并未涉及 $Re \left [ \lambda _{i} \right ] \leq 0$ 的情况，因为当存在某些 $\lambda _{i}$ 使得 $Re \left [ \lambda _{i} \right ] =0$ 时，线性化不能确定平衡点的稳定性。同时，定理1给出的结论是局部的，没有给出吸引域的相关信息，也不能判断全局稳定性，下面利用Lyapunov函数对上述结论进行扩展。

定理2：设 $D\subset R^{n}$ 是包含原点的一个区域，f(x)是定义在D上的局部Lipschitz函数，且f(0)=0。假设V(x)为D上的连续可微函数，且对所有域D成立

$k_{1}\left \| x \right \|^{a}\leq V(x)\leq k_{2}\left \| x \right \|^{a}$

$\dot{V}(x)\leq -k_{3}\left \| x \right \|^{a}$

其中，a、k1、k2、k3为正常数，则原点是系统的指数稳定平衡点，如果上述条件对全局成立，则原点是全局指数稳定平衡点。

对于线性系统 $\dot{x}=Ax$ ，可以采用二次型Lyapunov函数 $V(x)=x^{T}Px$ ，其中，P为实对称正定矩阵，应用定理2，V沿着 $\dot{x}=Ax$ 的轨线的导数为：

$\dot{V}(x)=x^{T}P\dot{x}+\dot{x}^{T}Px=x^{T}(PA+A^{T}P)x=-x^{T}Qx$

其中，Q定义为 $PA+A^{T}P=-Q$ （Lyapunov方程）

如果Q是正定的，由于 $\lambda _{min}(P)\left \| x \right \|^{2}\leq x^{T}Px\leq \lambda _{max}(P)\left \| x \right \|^{2}$ ，应用定理2，可以推断出原点是全局指数稳定的，即A为Hurwitz矩阵(因为定理1的条件是充要的)。直接应用Lyapunov定理可以得出原点是渐进稳定的，而对于线性系统，渐进稳定和指数稳定是等价的，因此也能推断出同样的结论。下面的定理3给出了基于Lyapunov方程的解判断原点指数稳定性的方法。

定理3：当且仅当对于任意一个正定对称矩阵Q，存在一个正定对称矩阵P满足Lyapunov方程 $PA+A^{T}P=-Q$ ，则矩阵A是Hurwitz的。而且，如果A为Hurwitz矩阵，则正定解P是唯一的。

定理3的结论帮助我们采用线性化的方法研究非线性系统。考虑非线性系统 $\dot{x}=f(x)$ ，其中f(x)是连续可微的，且f(0)=0，则在原点的邻域内可以描述为：

$\dot{x}=(A+G(x))x$

其中， $A=\frac{\partial f}{\partial x}|_{x=0}$ ，且当 $x\rightarrow 0,G(x)\rightarrow 0$ 。

当A为Hurwitz矩阵时，取Q为正定矩阵，由定理3知，求解Lyapunov方程可得到唯一的正定矩阵P。用 $V(x)=x^{T}Px$ 作为非线性系统的备选Lyapunov函数，则

$\dot{V}(x)=-x^{T}Qx+2x^{T}PG(x)x$

由于当 $x\rightarrow 0,G(x)\rightarrow 0$ ，给定任意正常数k<1，总能找到r>0，使得在域 $D=\left \{ \left \| x \right \|< r \right \}$ 内有 $2\left \| PG(x) \right \|\leq k\lambda _{min}(Q)$ ，因此在D内满足：

$\dot{V}(x)\leq -(1-k)\lambda _{min}(Q)\left \| x \right \|^{2}$

应用定理2可知原点为非线性系统的指数稳定平衡点。

3.吸引域

定义：设原点为系统 $\dot{x}=f(x)$ 的渐进稳定平衡点， $D\subset R^{n}$ 是包含原点的一个区域，f(x)为定义在D上的局部Lipschitz函数，则原点的吸引域是这样的一个集合：如果 $x_{0}\in D$ 在吸引域内，那么对于所有 $t\geq 0$ ，系统 $\dot{x}=f(x),x(0)=x_{0}$ 的解存在，且随着时间趋于无穷，解收敛到原点。

通常仅仅确定系统又渐进稳定的平衡点是不够的，还要确定系统在多大的区域是渐进稳定的，即确定该平衡点的吸引域，下面结合上述结论对利用Lyapunov方法估计吸引域。

根据Lyapunov方法，我们或许会认为：只要证明了在区域D内满足了公式(1)(3)，那么平衡点的吸引域估计显然就是区域D。但这种推测并不正确：尽管始于D内的轨线从一个Lyapunov面移动到更内部的Lyapunov面，但却没有保证轨线永远在D内。一旦轨线离开D，就不能保证 $\dot{V}(x)$ 为负值，从而V（x）衰减到0的结论就难以成立。

如果能保证始于D内的轨线始终在D内就不会出现上述问题。取集合 $\Omega _{c}=\left \{ V(x)\leq c \right \}$ 且使 $\Omega _{c}\subset D$ 。若初值在集合 $\Omega _{c}$ 内，那么由于 $\dot{V}(x)< 0$ ，会有 $V(x(t))< V(x(0))\leq c$ ，即轨线始终在集合 $\Omega _{c}$ 内，此时 $\Omega _{c}$ 就是一个吸引域的估计。