梯度的定义如下:
梯度是一个向量,也叫矢量。其方向为变化最快的那个方向,其大小就是那个方向的变化率。
为了描述这一变化率,我们用的是方向导数。
比如这个,曲面上的点沿着C1移动的变化率,就是函数f在其方向u1上的方向导数。


梯度推导
而我们要找的梯度,其方向就是方向导数中的最大者的方向;其值就是函数在此点处沿这个方向运动时的变化率。
而我们知道,在可微分的情况下,方向导数可以被偏导数线性表示。
下面这个是全微分的表达式。即函数对x的偏微分+函数对y的偏微分。
而这里的alpha和beta是函数的两个偏导数与方向向量u的夹角。

现在只要找到变化率![]() 的最大值,那就找到了梯度!
的最大值,那就找到了梯度!
因此我们将方向导数这个代数式进行变形。
改写为向量点积的形式。
那么这个式子就说明,方向导数![]() 是向量v在eu上的投影。
是向量v在eu上的投影。

假设两向量的夹角为theta。
显然theta不断接近于0时,向量v在eu方向上的投影![]() 也不断扩大。
也不断扩大。

当eu与v同向时,所得投影获得最大值。这说明向量v的模长即为方向导数中的最大者。

所以得到如下式子:
i和j分别是x轴和y轴的单位向量。为原点做正交分解后得到的单位向量。

梯度定义如下:

倒三角这个被称为微分算子,读作nabla。之后还会文章来讲。
梯度的优势
它的优势就是能表示所有的方向向量。
我们回到刚刚推导的式子。它等于梯度在其方向向量上的投影。


这个符号表示的是函数f在点(x0,y0)处的梯度的模(范数)。通常使用欧几里得范数(也称为 L2 范数)来计算,即:
梯度的模可以用来衡量函数在某个点的变化率。
回到推导
当θ等于2分之pi时。eu与梯度正交。此时方向导数为0

当θ等于pi时,eu与梯度的方向相反,此时方向导数最小,其值为梯度模长的相反数。








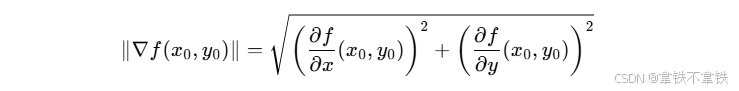
















 9212
9212

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








